ふたつの複素数。どちらかに絞ることで見てくる戦略【２０１８年数学】

今回は、２０１８年の九大理系数学の問題を解説します。
問題はこちら。

短い問題文ですが、だからこそやっかいな問題でもあります。短いと情報が少なく、手掛かりが見えにくいからです。本問は、受験生に解いてもらうと、解いた人の感想が割れる問題でもあります。方針が見える人と全くと言っていいほど見えない人に分かれるからだろうと思います。

その意味でも着眼点が重要な問題でもあります。

本問は、αとｚが複素数と示されています。２変数関数の処理と同様に、どちらかに絞ることが重要です。では、αなのか、ｚなのか。ここが最初の分岐点です。

迷ったときは、本問はｚの複素数を求めよと言っているので、ｚで整えていく方針でいいと思います。

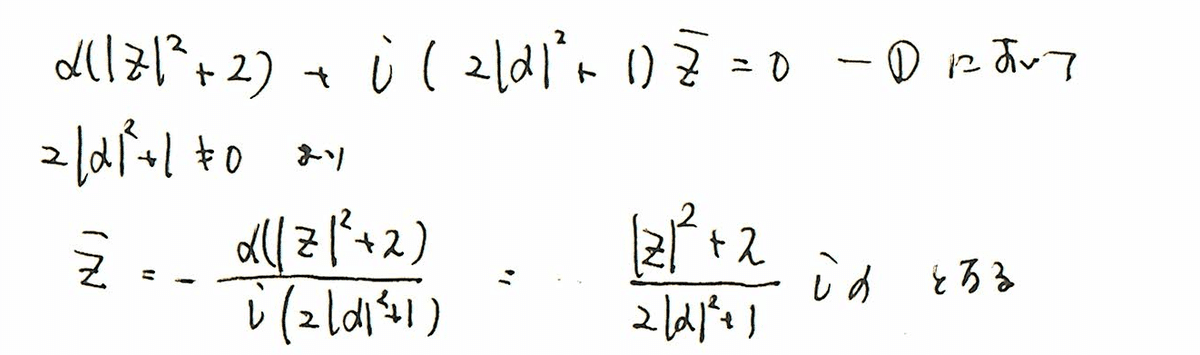
ここで、得られた式をしっかりと吟味しましょう。αは複素数なので、

であることを大切にしましょう。文字において、見やすく整えると、↓のような展開が見えてきます。

ここでｚとｚ（バー）がαで表せることはとても大きな情報となります。

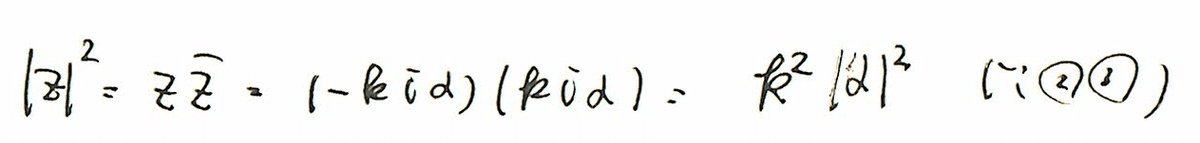
となるからです。ここまでくるとαを求められるとありがたいなと感じることができるでしょう。
当然、①式に戻してαを特定していく流れになります。

となります。ｋでまとめるか、αでまとめるか迷ってもいいと思います。αでやってみてダメならｋでやればいいだけのことです。

あとは、α＝０，α≠０で場合分けをしていきます。

となり、

となります。

本問は、α、ｚの複素数をどちらかに絞っていくという方針が大切な問題だったかなと思います。このような差が付く問題をしっかりと拾っていくことが合格につながるのではと思います。