
SGDK学習メモ:No.9、三角関数とテーブル化を学習してみる
*以下SGDKは記述時点で最新版のSGDK 2.00 (january 2024)を使用しています
SGDK学習の際のメモです。
が、今回の主な内容は三角関数関連です。
今回学習のベースにするのは(また)Hidecadeさんの
メガドライブ用ソフトのプログラミング その 17 - 三角関数とテーブル化 | Arcade Cabinet
です。非常に参考になりました。
今回の後半の内容はほぼHidecadeさんのサイトのままなのですが、実際にコードを書いて挙動の確認を行いました。Hidecadeさんのサイト中で一部理解できない処理があったのですが(ビット演算部分、後述)、そこは自分で解釈できるように処理を変更しました。
またコード記述前に三角関数の再学習も行いました。
毎度で恐縮ですが内容が冗長なのは仕様ということでご了承ください(無類の不器用/免罪符)。
三角関数、単位円の再学習
今回事前に三角関数について再学習を行いました。学習は主に
中学数学からはじめる三角関数
で行い、不明瞭な部分や忘れていることについては随時検索を行いました。
実際にコード化する際には三角関数だけでなく単位円(半径が1)を理解しておくと
・X座標がcos
・Y座標がsin
という考え方がわかり、今回の「三角関数とテーブル化」も理解がスムーズになるのではないでしょうか。上記の動画でも単位円について解説しています。
数学の単位円におけるX座標、Y座標とプログラミングにおけるX座標、Y座標について
数学の単位円では0°<θ<90°の場合、座標軸的に右上がX座標(cos)、Y座標(sin)共にプラスとなっています。
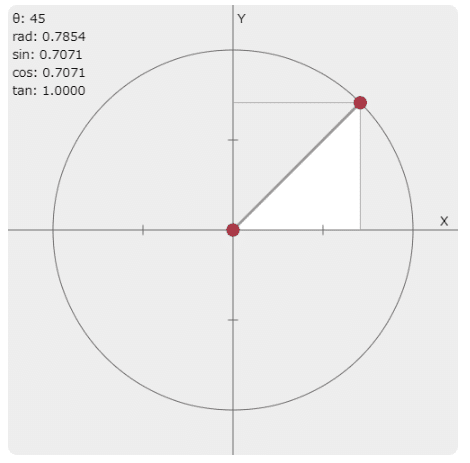
45°の場合、
X座標(cos)、Y座標(sin)共にプラス
90°<θ<180°は座標軸が左上になりX座標(cos)がマイナス、Y座標(sin)はプラスとなります。
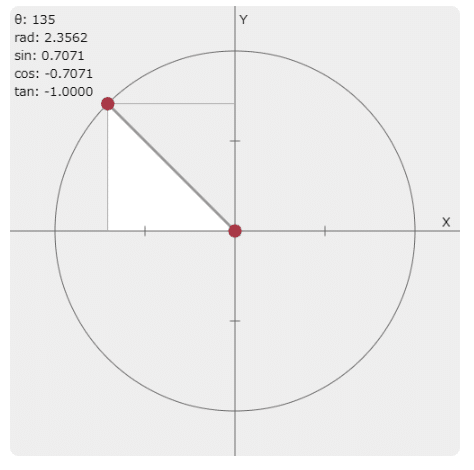
135°の場合、
X座標(cos)はマイナス、Y座標(sin)はプラス
角度が増えると左回りに座標が移動していきます。
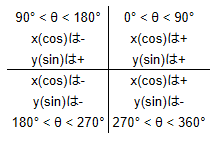
しかしながら画面が2次元での(ゲーム)プログラミングでは
右に行くとXが増加、「下」に行くとYが増加
です。
仮に画面上のスプライトを右下に移動させるとした場合

Excel等の表計算ソフトの
行番号、列番号も同じような考え方です
となり、左下に移動だと

となり、角度は右回りで増加していきます。
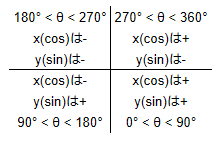
回転方向が逆(右回り)になる
後に行う角度のテーブル化は、この右回りを踏まえて作成する必要があります。
三角関数を使用しないで斜め移動することを考えてみる
仮に速度8、スプライトの移動する方向が「水平方向の左右」または「垂直方向の上下」の場合、毎フレームごとに8ドット移動する処理があると仮定します。
*ここでの速度8に深い意味はありません、現在テスト用に使用している速度が8なので同じ値にした、というだけです
現在『モトス』のタイトル画面をサンプルにプログラムを書いている途中なので、モトス(自機)の位置に流星が落ちてくる処理を例として考えてみます。まずは簡単な例から。
流星が真横に移動する場合。
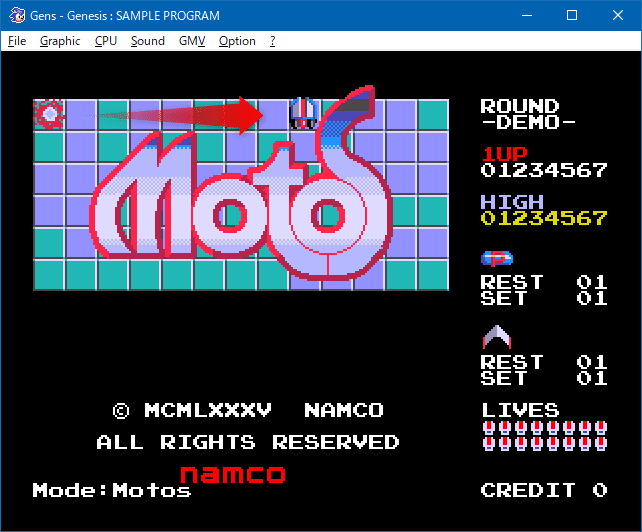
真下の場合。
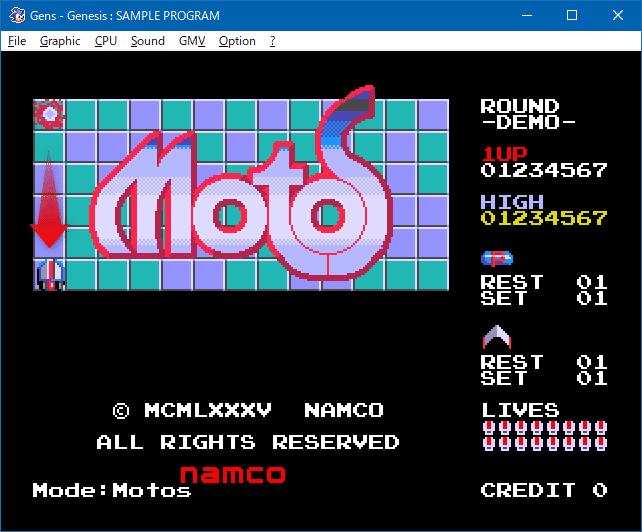
これらの場合は流星のX軸方向かY軸方向に+8(逆方向なら−8)するだけなので簡単です。
問題は斜めの場合です。今回は角度を斜め45°、XとYの両方に+8する、としてみます。
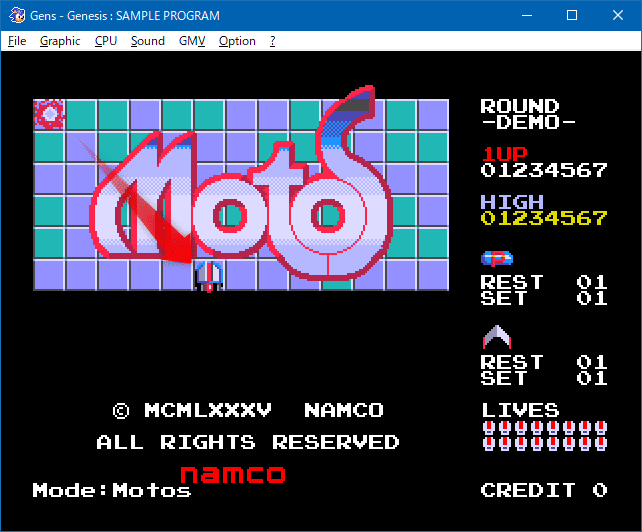
としてみる
45°は有名角の三角比の一つで、辺の比は1:1:√2になります。
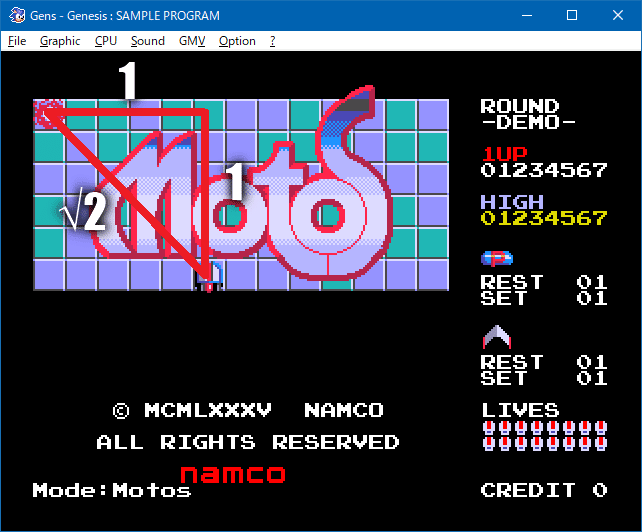
三角比を説明するための図です
今回の速度は8なので(比なのであまり意味はないのですが)8倍すると
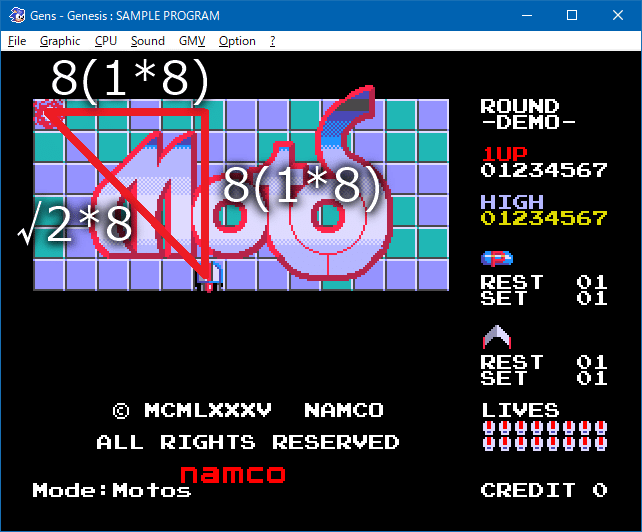
X+8とY+8の両方が行われると
√2倍になる
となり、√2≒1.414 → 8 * 1.414(=11.312)、つまり真横(X+8)や真下(Y+8)と比較すると「X+8かつY+8」は約1.4倍速い(移動距離が長い)、となります。
ドラクエ8などのRTAで使用される√2走法(ブラ走法)の移動速度が約1.4倍速い理由はこれです(と私は理解しました)。
では45°で真横や真下と同じ速度で移動するためにはX、Yにどのような値を設定すればよいのか。
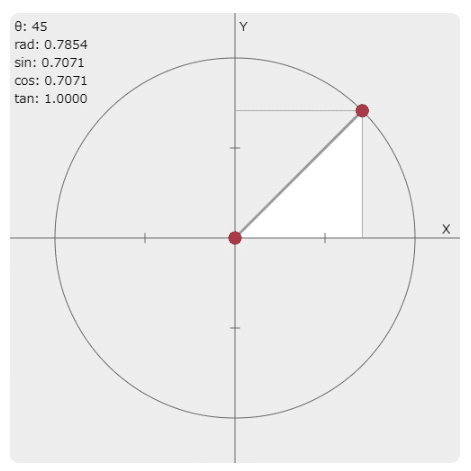
X は 8(速度) * 0.7071(cos) ≒ +5.6
Y は 8(速度) * 0.7071(sin) ≒ +5.6
となります。
ここまで角度が0°と90°(速度*1)、45°(速度*0.701)の説明を行いましたが、三角関数を使用することで更に多くの角度に対応することが可能になります。
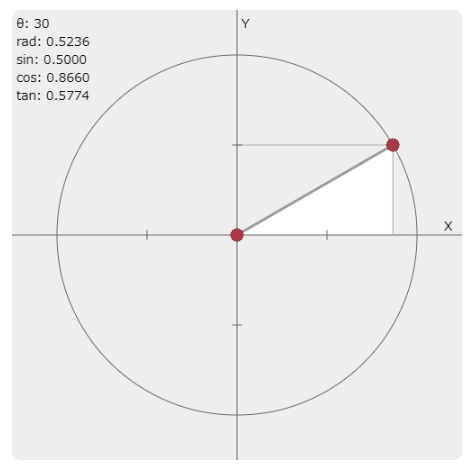
30°の場合
モトスと流星の角度が30°の場合
X = 8*0.866(cos) = +6.928
Y = 8*0.5(sin) = +4
となります。
30°も有名角の三角比 1:2:√3(1.732) なのでこれで検算してみると
X = 8*(√3/2) ≒ 4*1.732 = +6.928
Y= 8*(1/2) = +4
と上の計算と合致します。
三角関数をテーブル化する
*私のUnityの知識、経験はHello Worldだけです、以下のC#の説明に間違いがあったらごめんなさい
現在のモダンな開発環境、例えばUnityでC#の場合、三角関数の計算は簡単です。
(角度/dgreeではなく)ラジアン/radianを求める場合は
float GetAngle(Vector2 start,Vector2 target)
{
Vector2 dt = target - start;
float rad = Mathf.Atan2 (dt.y, dt.x);
float degree = rad * Mathf.Rad2Deg;
return degree;
}https://t-stove-k.hatenablog.com/entry/2018/08/27/153609
終点から始点を引いたyとxをMathf.Atan2()に渡すだけです。
またsin、cos(そしてtan)も
Debug.Log(Mathf.Sin(rad)); // -> 0.5
Debug.Log(Mathf.Cos(rad)); // -> 0.8660254
Debug.Log(Mathf.Tan(rad)); // -> 0.5773503https://www.midnightunity.net/unity-mathf/
Mathf.Sin()、Mathf.Cos()にラジアンを渡すだけです。
翻ってSGDK+C言語の場合、上記のような便利な関数がありません。ゴリゴリにロジックを書くこと自体は可能ですがメガドライブには負荷が高めです(メガドライブのメインCPUはMC68000の7.67MHz、PALだと7.60MHzになるようです)。
そこで角度を粗くした独自の角度を決め、それを配列化(「角度テーブル」)。更にsin、cosを事前に計算して配列化(「sinテーブル」「cosテーブル」)。
角度テーブルの値からsinとcosを取得、という流れになります。
そこで、「MSXの適当手帳」さんのサイトに書いてあった、「レーダー法」という手法を参考に角度の計算をすることにしました。画面を格子状に分割し、オブジェクトがどの格子にあるかで、角度を判断する方法です。
まず、レトロゲームにおいては細かい角度までの計算は必要ないと判断し、360度を32段階(8の倍数)にして、上図のように角度を0-31の独自の単位で扱うことにします。例えば真上の場合は「24」、真下は「8」となります。
MSXの適当手帳へのリンク、改行とBold装飾を追加
今回"360度を32段階"は踏襲しました。
角度の計算を配列で読み出すためのテーブルを作成。円の中心が基準となる座標です。
画面を16ドット×16ドット単位で分割することを想定。それぞれの位置の配列に角度(0-31)を格納格子のサイズを小さくし、角度も細かく分割すれば精度が上がりますが、処理速度が遅くなります。
これは少し手を加えました。
Hidecadeさんは40 cell wide mode(H40)を分割、つまり
40*28 CELL (320*224 PIXEL)を16ドット単位で分割 → 20 * 14
です。
今回の私の『モトス』ではプレイフィールドの幅を30CELLとしているので
30*28 CELL (240*224 PIXEL)を16ドット単位で分割→ 15 * 14
としました。
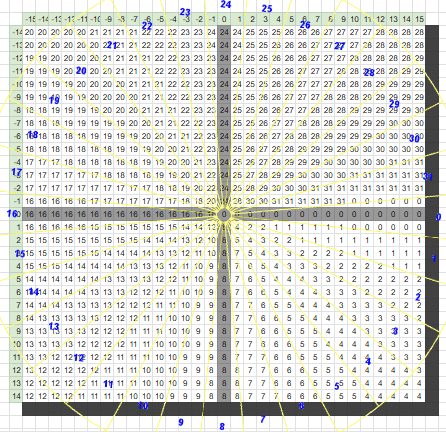
この図を配列に落とし込みます。

ここからがわからない部分です。Hidecadeさんのロジックだと角度テーブル(TABLE_ATAN2)から値を取り出すのに
s16 index = ( X | 320) / 16 | ( Y | 224) / 16 * 41;としています。XとYの | が「ビット演算でorしている」ことはわかるのですが「なぜこのロジックでインデックスを特定できるのか」が理解できませんでした(無類の不器用)。
これで嫌になって手を止めると今までと同じく中途半端で投げ出すことになってしまうので、今回は
s16 index = ((X差分/16) + 15) + ((Y差分/16) + 14) * 31);としました。
角度が取れるようになったので、次はcosとsinのテーブルを作成します。表計算ソフト(今回はGoogleスプレッドシートを使用)で計算を行い、それを配列にします。

rad = ROUND(RADIANS(360*(独自角のdegree/32)),4)
cos = ROUND(COS(rad),4)
sin = ROUND(SIN(rad),4)

上図にあるように一応計算(確認)しました
これで角度テーブルの値からcos、sinを取得 → cos、sinに速度を掛けるとXとYの移動量が導き出せる、となります。
実際に動かしてみる
テスト中の『モトス』にテーブル化した三角関数を組み込み、モトス(自機)に流星が落ちてくる動作を確認してみます。
(アニメーションgifにしたかったのですが相変わらずアップロードに失敗するのでYouTubeにしました、この問題は数年以上放置されている気がしますが、できればエラーコードや理由の表示、または受け付けるアニメーションgifの明確な仕様を公表してほしいところです)
スタートボタン押下→スピード8の設定で流星がモトスに近づく挙動となっています(=毎フレームごとの処理になってはいません)。
それっぽい挙動になっていますが実は問題があります。
モトスと流星の位置関係によっては、流星がモトスとズレた位置に移動します。
今回は角度を32段階にしている=角度が荒いため、流星が正確なモトスの位置に移動できない場合があります。いわゆる安地(安置)が発生します。
流星は直進します=モトスの位置とはズレます
今回の三角関数のロジックを使用して、確実にモトスの位置に流星を移動させるには補正処理が必要になります。
最初に試みたのは、整数演算だけで目的の方向への軌道を計算できる方法であるDDA(Digital Differential Analyzer)という手法を試みました。
「・X方向とY方向のうち目標までの座標の差分が大きいほうは毎回移動させる ・差分が短いほうについては誤差diffが蓄積した時だけ移動させる」**松浦健一郎/司ゆき『シューティングゲーム アルゴリズム マニアックス』より引用
敵機の発射される弾の軌道をこの手法で実装していたのですが、メリットとデメリットがありました。計算が高速で、確実に目標地点に到達することがメリットですが、角度によって速度が変わるデメリットがありました。
流星の処理においては、この"確実に目標地点に到達"できる処理のほうが向いている感じです。
(『シューティングゲーム アルゴリズムマニアックス』は図書館に全然置かれていません、旧版は市場価格がそこそこ安いので買ってみようかな)
*2024/06/21追記
三角関数のロジックを利用して、モトスの周りで流星を回転させてみました。
【了】
