【解説】統計検定 2019年準1級 問8

問題本文

問題本文は公式サイト又は公式問題集を参照してください。

問題解説（1）

【問題要約】
217点の観測データをFusedLasso回帰を用いて平滑化を行う。
この時、平滑化を行った結果の図として適切なものを答えよ。なお、FusedLasso回帰は以下の式を用いるものとする。

（結果の図は公式問題集を参照してください）

【回答】
④の図（グラフの各所が水平の図）

【解説】
本問ではFusedLasso回帰を用いた正則化の結果を尋ねています。
FusedLasso回帰を知らなくても、数式の意味さえ理解できれば解ける問題のため、数式の第1項(赤色)と第2項(青色)に分けて見ていきましょう。

まず前提として、βiは hat βを最小にする値の集合になります。

そのため、第1項だけを見ると "yi = βi" が最適解となります。
これはすなわち、βiの値は観測データの値そのものになります。

次に第2項だけを見ると "β1 = β2 = ... = β217" が最適解となります。
こちらはβiの値が全て同じになるため、X軸と並行なグラフになります。

FusedLasso回帰では、第1項と第2項のバランスをλによって調整します。
また、第1項と第2項の値は以下の性質を持ちます。

第1項: 調整データβiと観測データyiの差の二乗
第2項: 調整データβiと一つ先の調整データβi+1の差の絶対値

『βiとyiの差』と『βiとβi+1の差』が同じ時
差が1よりも大きい: 第1項 > 第2項
差が1よりも小さい: 第1項 < 第2項

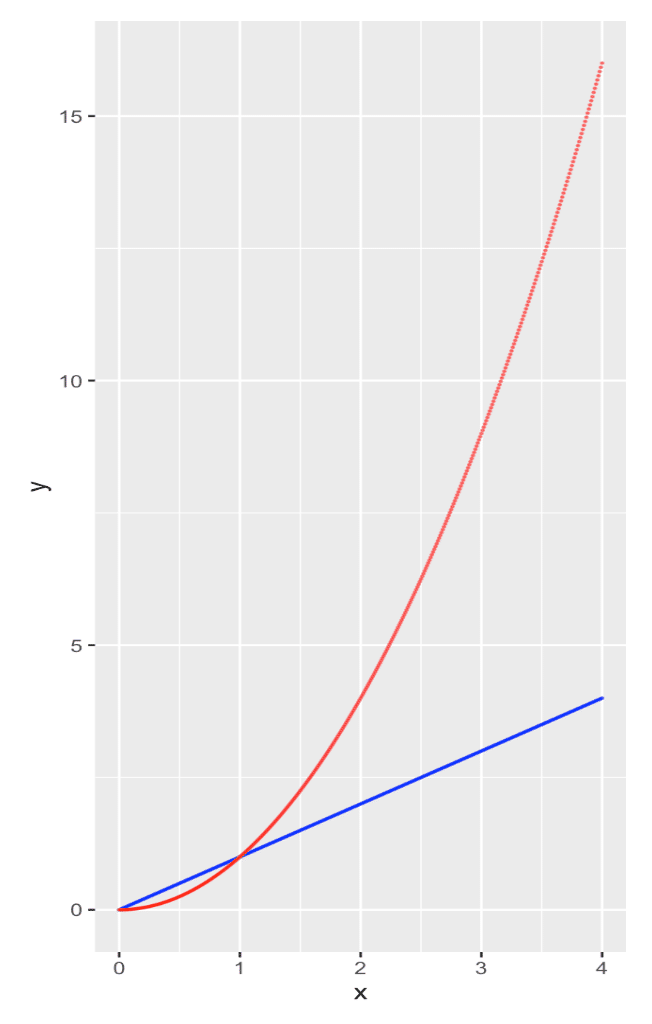
以上の性質から、

『yi と yi+1の差』が大きい時
第1項(yi - βi)の方が第2項(βi+1 - βi)よりも小さくなるように補正する。

『yi と yi+1の差』が小さい時
第1項(yi - βi)よりも第2項(βi+1 - βi)の方が小さくなるように補正する。

また、第1項(赤色)の値は差が0に近付くほど無視できるようになりますが、第2項(青色)の値は下がり幅が常に一定のため、第2項の値は0になりやすいという性質があります。

第2項の値が0の時、βi = βi+1となります。
この状態を図で表すと、グラフがX軸と水平になるため、④の図（グラフの各所で水平の図）が答えとなります。

問題解説（2）

【問題要約】
（1）と同じ観測データに対して別の平滑化手法を適用した。
この時、新たに生成された図と一致する平滑化手法を答えよ。

（結果の図は公式問題集を参照してください）

【回答】
④の式

【解説】
本問は選択肢を見て、即座に①②③が間違いだと分かります。
その理由は、それぞれの第2項がβiの2乗 又は βiの絶対値になるため、最適解がどちらも "βi = 0" となります。

そのため、βiの値は全体的に0に近付くはずです。
しかし、今回提示された図のY軸に注目すると、観測データのY軸とほとんど変化がありません。

ここから、先にも述べた通り①②③が選択肢から除外されます。

次に④が答えになる理由ですが、④の第2項を以下の通り変形します。

これは『「今回の差」と「前回の差」の差』を表しているため、言い換えると『傾きの差』を表していることになります。

また（1）と同様の理由により、第1項よりも第2項の方が0なりやすい性質があります。

そのため、傾きの差が0になりやすくなります。
傾きの差が0とは、前回と傾きが同じであることを意味するため、グラフ上では直線で表現されます。

以上の理由により、直線が多い（区分線形である）本問のグラフは、④の式から生成されたものと分かります。

ちなみに、⑤の式は以下の通り変形できます。

これは『「今回の傾きの差」と「前回の傾きの差」の差』を表しているため、言い換えると『変化の差』を表しています。

直線と曲線が入り混じれるグラフになると思いますが、区分線形なグラフにはならないと分かるため、間違いだと分かります。