統計検定準1級 2021年解説 問2-2(最尤推定量)
問題本文は公式サイト又は公式問題集を参照してください。
【問題要約】
ある機械が故障するまでの時間Xは平均λの指数分布に従う。この時、λ = 1/a と仮定した時の分散はa^2である。分散の最尤推定量を求めよ。
なお、必要に応じて指数分布の確率密度関数を参照してもよい。

【回答】

【解説】
本問では最尤推定量に対する理解と計算能力が問われています。
必須知識
最尤推定量とは、尤度関数を微分した式の結果がゼロ(最大値)となる方程式を解くことで求まる推定量を指します。
また、尤度関数とはn個の確率関数から求まる関数になります。
計算
本問では、n台の機械が故障するまでの時間が、それぞれ独立に指数分布に従うと仮定する為、尤度関数は以下の通りとなります。
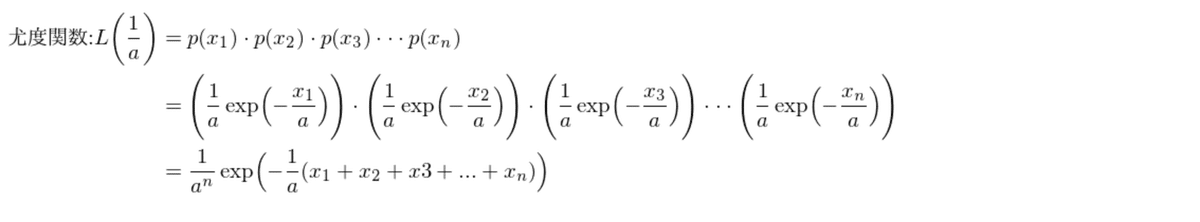

上で求めた対数尤度関数を微分して、答えがゼロとなる方程式を解く必要がある為、以下の手順で計算を進めます。

平均1/aの指数分布の期待値E[X]はa, 分散V[X]はa^2になります。
その為、求めた期待値の最尤推定量の2乗が分散の最尤推定量になります。
