
【解説】統計検定 2019年準1級 問1(ポアソン分布)
問題本文
問題本文は公式サイト又は公式問題集を参照してください。
問題解説(1)
問題要約
得点XとYはそれぞれ独立にポアソン分布に従う。
Xの期待値が3、Yの期待値が2の時、X+Yの期待値と分散を答えよ。
回答
期待値: 5
分散: 5
解説
本問ではポアソン分布に関する基礎的な知識が問われています。
本問に正解する為にはポアソン分布に関する以下の知識が要求されます。
期待値と分散はパラメータλの値と一致する
再生成を持つ
1. 期待値と分散はパラメータλの値と一致する
Xがポアソン分布に従う時、Xの期待値と分散はポアソン分布のパラメータλの値と一致します。

ここから得点Xの期待値と分散は3、Yの期待値と分散は2になります。

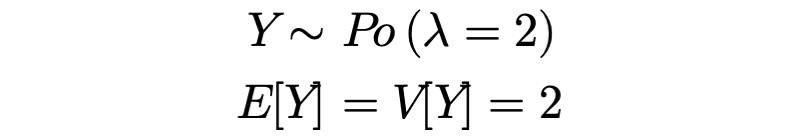
2. 再生性を持つ
再生性とは『個々のパラメータから生成した確率変数の合計』と『合計したパラメータから生成した確率変数』が一致する性質を指します。

以上の2つの性質からX+Yの期待値と分散は5となります。

問題解説(2)
問題要約
得点XとYが(1)と同じポアソン分布に従うものとする。
この時、X+Yの観測値が4であった。Xが従う分布と期待値を答えよ。
【ヒント】
ポアソン分布の確率質量関数は以下の式を用いて良い。

回答
Xは期待値が2.4の二項分布に従う
解説
本問では問題から適切な分布を選択する技術が問われています。
勘所さえ掴めていれば、難しい計算を飛ばして答えに辿り着けます。まずはその勘所を押さえて答えを求めてみましょう。
XとYの合計得点が4であり、期待値は X:Y = 3:2 となります。
ここから、合計得点を試行回数と置き、Xの得点を成功、Yの得点を失敗とみなした時、Xは以下の二項分布に従います。

また、二項分布に従うXの期待値は以下の通りとなります。

丁寧な解説
答えは既に出しましたが、問題文で提示されたポアソン分布の確率質量関数を用いた方法でも答えを求めてみましょう。こちらの方法で正解する為には以下の知識が要求されます。
二項分布の確率質量関数
条件付き確率の計算(技術)
【注意事項】
ポアソン分布の確率質量関数から二項分布の確率質量関数を導出します。
以上の前提をもって以降の解説をご覧ください。
1. 二項分布の確率質量関数
次節の条件付き確率の計算では、以下に示す二項分布の確率質量関数を導出する流れになります。

2. 条件付き確率の計算
条件付き確率の計算を行うにあたり、まずは数式を用意します。求めたい値は X+Y = 4 の時のXの確率関数になります。 X = x の時、必ず Y = 4-x となる点に注意してください。


用意した数式を展開した式が以下になります。

式の展開の解説
1 ~ 3行目: 各色(赤・青・緑)が各行で対応します
1行目: 条件付き確率を式で表す
2行目: ポアソン分布を確率質量関数で表す
3行目: 分数を整理する
4行目: ネイピア数(e)を約分します
5 ~ 6行目: 各色(赤・青)が各行で対応します
5行目: 約分後の式を整理する
6行目: 更に式を整理する(詳細は後ほど解説)
6行目: 赤字部分の解説
二項係数(あるいはコンビネーション)と呼ばれる操作になります。
『二項係数』で検索すると丁寧な解説がたくさん見つかるため、ここでの解説は省略します。
6行目: 青字部分の解説
分母と分子で指数の合計が同じ時、分母で分子を割ることができます。
具体例を1つ用意したので、以下の式を参照してください。

展開式の結果を確認すると、二項分布の確率質量関数と一致します。
よって、二項分布に従うXの期待値は 4×0.6 = 2.4 となります。
