【解説】統計検定 2019年準1級 問4

問題本文

問題本文は公式サイト又は公式問題集を参照してください。

問題解説（1）

【問題要約】
ある商品について、CMの影響と購入の有無について調査を行った。この時、CMの影響あり且つ購入ありの期待値を答えよ。
尚、調査の結果は以下の表の通りである。

【回答】
85.5名

【解説】
本問は独立性について尋ねています。
独立性とは、CMの影響と購入の有無には全く関係がないと仮定したものであり、その時の値（期待値）を求めます。

期待値は以下の方法で導くことが可能です。

Point: 丁寧な期待値の求め方
期待値を求めるには、まず割合を求める必要があります。
例えば左上の値（CMの影響あり×購入あり）を求める場合、CMの影響ありが45%(= 135/300)、購入ありが63.3%(= 190/300)になるため、CMの影響を受けて購入したのは全体の28.5%(= 45%*63.3%)になります。
その後、割合に総数を掛けて85.5名(= 28.5%*300名)が求まります。

改めて式に直すと『(135/300)*(190/300)*300』となり、この式を整理すると『(135*190)/300』となります。

よって、CMの影響あり×購入ありの期待値は85.5名となります。

問題解説（2）

【問題要約】
CMの影響の有無と購入の有無の関連性に関するピアソンのカイ二乗統計量を答えよ。

【回答】
3.26

【解説】
カイ二乗統計量を求めたいが、今回は独立性の検定基準が適用できるため、そちらの公式に当てはめて計算を行います。

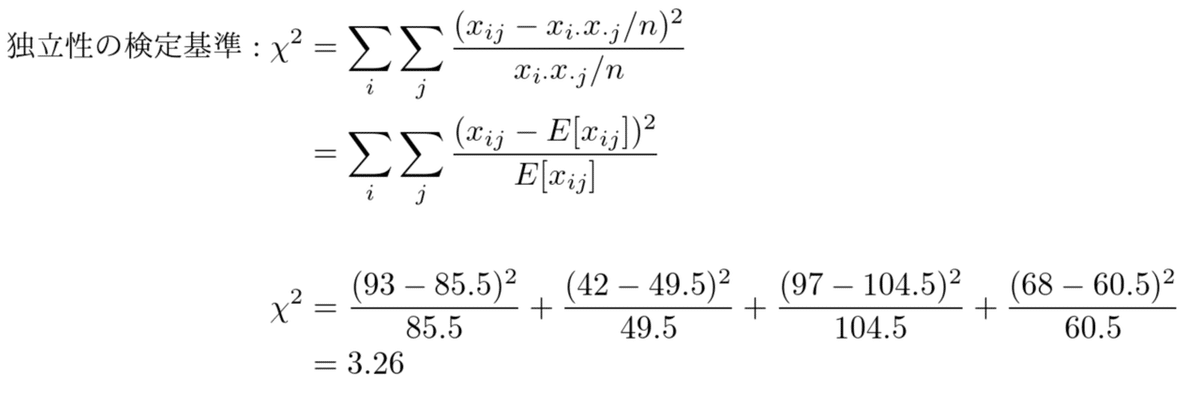
よって、カイ二乗統計量は3.26となります。

問題解説（3）

【問題要約】
「CMの影響の有無と購入の有無には関連性がない」という帰無仮説に対する片側検定の結果を答えよ。

【回答】
有意水準10％で棄却されるが、5％では棄却されない。

【解説】
（2）の問いでカイ二乗統計量を求めたため、カイ二乗分布表を参照することで答えを導くことが可能です。

この時、自由度と呼ばれる概念が登場しますが、調査表の『(行-1)×(列-1)』で求めることができます。本問では2行(CMの影響の有無), 2列(購入の有無)になるため、『(2-1)×(2-1) = 1』で自由度は1になります。

自由度1のカイ二乗分布表を参照した結果、有意水準10%, 5%, 2.5%, 1%の値はそれぞれ以下の通りでした。

よって、3.26は有意水準10％では棄却されるが、5％では棄却されないことが分かります。