
Newton力学② 位置の表し方
前回の記事はこちら↓
必要な前提知識はこちら↓
・ベクトル,行列とベクトル解析(準備中……)
さて,Newton力学の第2回です。
今回は,力学で欠かせない,”座標”の表記について見ていこうと思います。
(今回から数式表記が必要となるため,一部TeXを使っています。表記に不具合がある場合は,この記事にコメントいただくか,筆者Twitter(@SiN_JAPAN2022)までご連絡を。)
1次元の場合
1本の数直線[座標軸]をとって,その点に相当する実数値を"位置"とよぶ。
ただし,座標軸は必ずしも直線でなくてもよく,曲がっていてもよい。
(このことは,空間の一様性・等方性により保証される。)
また,軸方向の単位ベクトル(長さが1のベクトル)[基本ベクトル]$${\boldsymbol{e}_x}$$を用いれば,位置が$${x}$$のときの位置ベクトルは$${x\boldsymbol{e}_x}$$と表せる。

でも,曲がった座標軸だと,異なる運動ごとに別の軸をとらなければならないので扱いにくい。そこで,次元(位置を表すための情報量,すなわち座標軸の数)を増やす。まずは2次元の場合から。
2次元の場合
2本の座標軸をとり,基本ベクトル2つで位置を示す("斜交座標系")。
$$
\boldsymbol{r}=2\boldsymbol{e}_\alpha+3\boldsymbol{e}_\beta=\begin{bmatrix}\boldsymbol{e}_\alpha&\boldsymbol{e}_\beta\end{bmatrix}\begin{pmatrix}2\\3\end{pmatrix}
$$
座標軸が明らかなときは,省略して$${\boldsymbol{r}=\begin{pmatrix}2\\3\end{pmatrix}}$$と書いてもよい。
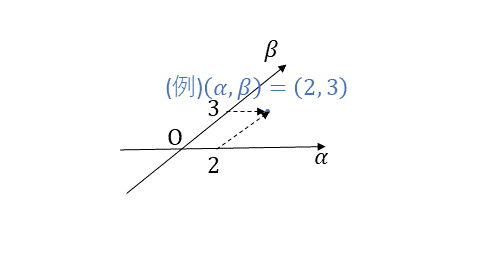
一般的には直交する座標軸が便利で,
①2次元Descartes(デカルト)座標系[直交直角座標系,Cartesian(カーテシアン)座標系]
②2次元極座標系[円座標系]
の二つがよく行われる。
①2次元Descartes座標系
いわゆる$${xy}$$平面。小学校時代から見慣れているはず。
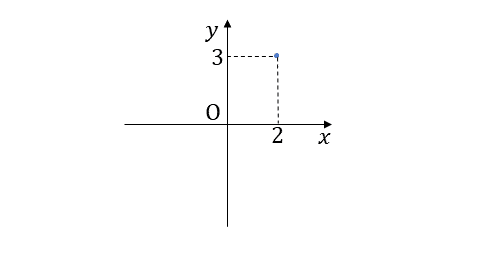
②2次元極座標系
原点からの距離$${r}$$と基準の半直線[始線](図では$${\mathrm{OX}}$$)からの角度$${\theta}$$(反時計回り)で位置を表す(下図参照)。ただし,$${0\le\theta<2\pi}$$という条件がつく。
下図の座標は,$${\boldsymbol{r}=\begin{pmatrix}4\\\frac{5}{12}\pi\end{pmatrix}}$$と表される。
(注: 厳密には$${\boldsymbol{r}\ne\begin{bmatrix}\boldsymbol{e}_r&\boldsymbol{e}_\theta\end{bmatrix}\begin{pmatrix}4\\\frac{5}{12}\pi\end{pmatrix}}$$なのでこの書き方は望ましくないのだが,便宜上用いられる。$${\boldsymbol{r}=\begin{pmatrix}r\\\theta\end{pmatrix}}$$と取り決めていると考えてもよい。)

ここで注意しなければならないのが,2次元極座標系では基本ベクトルが位置によって異なる,ということ。先ほどの図に基本ベクトルを重ねると,次のようになる。

数式で表すと,
$$
\frac{\partial\boldsymbol{e}_r}{\partial\theta}=\boldsymbol{e}_\theta
\\
\frac{\partial\boldsymbol{e}_\theta}{\partial\theta}=-\boldsymbol{e}_r
$$
(証明はベクトル解析(未公開)に譲る。)
さて,2次元Descartes座標系と2次元極座標系における位置の値[座標値]どうしを互いに変換する方法があると,便利である。
ここで,三角関数$${\sin{\theta},\ \cos{\theta}}$$が単位円(半径1の円)を使って下の図のように定義されていることを思い出そう。

そうすると,
$$
x=r\cos{\theta}
\\
y=r\sin{\theta}
$$
がわかる。
今2次元極座標系$${\begin{pmatrix}r\\\theta\end{pmatrix}}$$から2次元Descartes座標系$${\begin{pmatrix}x\\y\end{pmatrix}}$$への座標値の変換は求まったが,逆の操作が必要なこともあるはず。2式を連立すると,
$$
r=\sqrt{x^2+y^2}
\\
\theta=\arccos{\frac{x}{\sqrt{x^2+y^2}}}=\arcsin{\frac{y}{\sqrt{x^2+y^2}}}
$$
ここで,2次元Descartes座標系と2次元極座標系の,基本ベクトルどうしの関係を考えてみる。
$${\boldsymbol{e}_r}$$は,$${r}$$が増える方向の単位ベクトル,$${\boldsymbol{e}_\theta}$$は$${\theta}$$が増える方向の単位ベクトルだから,
$$
\boldsymbol{e}_r=\frac{\frac{\partial\boldsymbol{r}}{\partial r}}{\|\frac{\partial\boldsymbol{r}}{\partial r}\|}=\frac{\frac{\partial}{\partial r}(\boldsymbol{e}_x r\cos{\theta}+\boldsymbol{e}_y r\sin{\theta})}{\|\frac{\partial}{\partial r}(\boldsymbol{e}_x r\cos{\theta}+\boldsymbol{e}_y r\sin{\theta})\|}=\frac{\boldsymbol{e}_x\cos{\theta}+\boldsymbol{e}_y\sin{\theta}}{\|\boldsymbol{e}_x\cos{\theta}+\boldsymbol{e}_y\sin{\theta}\|}=\boldsymbol{e}_x\cos{\theta}+\boldsymbol{e}_y\sin{\theta}\\\boldsymbol{e}_\theta=\frac{\frac{\partial\boldsymbol{r}}{\partial\theta}}{\|\frac{\partial\boldsymbol{r}}{\partial\theta}\|}=\frac{\frac{\partial}{\partial\theta}(\boldsymbol{e}_x r\cos{\theta}+\boldsymbol{e}_y r\sin{\theta})}{\|\frac{\partial}{\partial\theta}(\boldsymbol{e}_x r\cos{\theta}+\boldsymbol{e}_y r\sin{\theta})\|}=\frac{-\boldsymbol{e}_x r\sin{\theta}+\boldsymbol{e}_y r\cos{\theta}}{\|-\boldsymbol{e}_x r\sin{\theta}+\boldsymbol{e}_y r\cos{\theta}\|}=-\boldsymbol{e}_x \sin{\theta}+\boldsymbol{e}_y \cos{\theta}
$$
この関係を行列で表すと,
$$
\begin{bmatrix}\boldsymbol{e}_r&\boldsymbol{e}_\theta\end{bmatrix}=\begin{bmatrix}\boldsymbol{e}_x&\boldsymbol{e}_y\end{bmatrix}\begin{pmatrix}\cos{\theta}&-\sin{\theta}\\\sin{\theta}&\cos{\theta}\end{pmatrix}
$$
また,右から逆行列をかけることにより,
$$
\begin{bmatrix}\boldsymbol{e}_x&\boldsymbol{e}_y\end{bmatrix}=\begin{bmatrix}\boldsymbol{e}_r&\boldsymbol{e}_\theta\end{bmatrix}\begin{pmatrix}\cos{\theta}&-\sin{\theta}\\\sin{\theta}&\cos{\theta}\end{pmatrix}^{-1}=\begin{bmatrix}\boldsymbol{e}_r&\boldsymbol{e}_\theta\end{bmatrix}\begin{pmatrix}\cos{\theta}&\sin{\theta}\\-\sin{\theta}&\cos{\theta}\end{pmatrix}=\begin{bmatrix}\boldsymbol{e}_r&\boldsymbol{e}_\theta\end{bmatrix}\begin{pmatrix}\frac{x}{\sqrt{x^2+y^2}}&\frac{y}{\sqrt{x^2+y^2}}\\-\frac{y}{\sqrt{x^2+y^2}}&\frac{x}{\sqrt{x^2+y^2}}\end{pmatrix}
$$
基本ベクトルの変換と座標値の変換は混同しやすいが,全くの別物。
次の例題を解いて,理解を深めよう。
[例題]
(1)2次元極座標系の例に挙げた,$${\boldsymbol{r}=\begin{pmatrix}4\\\frac{5}{12}\pi\end{pmatrix}}$$を,2次元Descartes座標系の座標で表せ。ただし,$${\sin{\frac{5}{12}\pi}=\frac{\sqrt{6}+\sqrt{2}}{4},\ \cos{\frac{5}{12}\pi}=\frac{\sqrt{6}-\sqrt{2}}{4}}$$を用いて,三角関数が残らない形にすること。
(2)あるベクトル関数$${\boldsymbol{F}}$$が$${\boldsymbol{F}=\begin{bmatrix}\boldsymbol{e}_r&\boldsymbol{e}_\theta\end{bmatrix}\begin{pmatrix}F_r\\F_\theta\end{pmatrix}}$$で与えられるとき,2次元Descartes座標系ではどのように表せるか。
[解答]
(1)
2次元極座標系から2次元Descartes座標系への座標値変換$${\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}r\cos{\theta}\\r\sin{\theta}\end{pmatrix}}$$より,
$$
\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}4\cos{\frac{5}{12}\pi}\\4\sin{\frac{5}{12}\pi}\end{pmatrix}=\begin{pmatrix}\sqrt{6}-\sqrt{2}\\\sqrt{6}+\sqrt{2}\end{pmatrix}
$$
(2)
基本ベクトルの変換より,
$$
\begin{bmatrix}\boldsymbol{e}_r&\boldsymbol{e}_\theta\end{bmatrix}=\begin{bmatrix}\boldsymbol{e}_x&\boldsymbol{e}_y\end{bmatrix}\begin{pmatrix}\cos{\theta}&-\sin{\theta}\\\sin{\theta}&\cos{\theta}\end{pmatrix}
$$
したがって,
$$
\begin{bmatrix}\boldsymbol{e}_r&\boldsymbol{e}_\theta\end{bmatrix}\begin{pmatrix}F_r\\F_\theta\end{pmatrix}=\begin{bmatrix}\boldsymbol{e}_x&\boldsymbol{e}_y\end{bmatrix}\begin{pmatrix}\cos{\theta}&-\sin{\theta}\\\sin{\theta}&\cos{\theta}\end{pmatrix}\begin{pmatrix}F_r\\F_\theta\end{pmatrix}=\begin{bmatrix}\boldsymbol{e}_x&\boldsymbol{e}_y\end{bmatrix}\begin{pmatrix}F_r\cos{\theta}-F_\theta\sin{\theta}\\F_r\sin{\theta}+F_\theta\cos{\theta}\end{pmatrix}
$$
この差異は,位置ベクトル$${\boldsymbol{r}\ne\begin{bmatrix}\boldsymbol{e}_r&\boldsymbol{e}_\theta\end{bmatrix}\begin{pmatrix}r\\\theta\end{pmatrix}}$$に由来している。
座標の値は$${x=r\cos{\theta},\ y=r\sin{\theta}}$$で,基本ベクトルは上のような変換で移る,ということを覚えておこう。
3次元の場合
一般論は割愛し,よく用いられる3種類の座標系についてみていく。
①3次元Descartes座標系[直交直角座標系]
2次元Descartes座標系に,$${xy}$$平面と直交する,いわゆる$${z}$$軸を追加したもの。$${z}$$軸の向きは2方向とれるが,右手の親指を$${x}$$軸方向,人差し指を$${y}$$軸方向に向けたとき,中指が自然に向く方向を$${z}$$軸の方向に定める(右手系)。
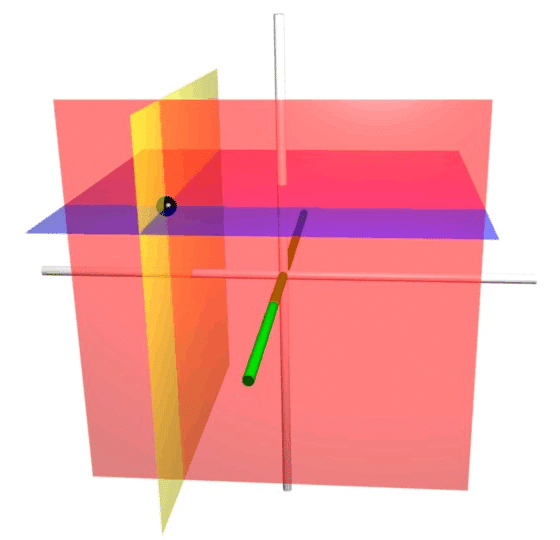
②3次元極座標系[球面座標系]
3次元極座標系は,図のような座標軸のとり方である。

③円筒座標系[円柱座標系]
2次元極座標系に$${z}$$軸を追加したもの。3次元極座標系における値と区別するため,$${\rho,\ \varphi,\ z}$$の3成分で表す。したがって$${0\le\varphi<2\pi}$$という条件は,そのまま残る。

座標値の変換に関しては,
$$
x=r\sin{\theta}\cos{\varphi}=\rho\cos{\varphi}\\y=r\sin{\theta}\sin{\varphi}=\rho\sin{\varphi}\\z=r\cos{\theta}=z
$$
$$
r=\sqrt{x^2+y^2+z^2}=\sqrt{\rho^2+z^2}\\\theta=\arccos{\frac{z}{\sqrt{x^2+y^2+z^2}}=\arcsin{\frac{\sqrt{x^2+y^2}}{\sqrt{x^2+y^2+z^2}}}}=\arccos{\frac{z}{\sqrt{\rho^2+z^2}}}=\arcsin{\frac{\rho}{\sqrt{\rho^2+z^2}}}\\\varphi=\arccos{\frac{x}{\sqrt{x^2+y^2}}}=\arcsin{\frac{y}{\sqrt{x^2+y^2}}}=\varphi
$$
$$
\rho=\sqrt{x^2+y^2}=r\sin{\theta}\\\varphi=\arccos{\frac{x}{\sqrt{x^2+y^2}}}=\arcsin{\frac{y}{\sqrt{x^2+y^2}}}=\varphi\\z=z=r\cos{\theta}
$$
これらの導出過程は割愛するが,そこまで複雑でもないので,一度自分で導いてみるとよい。
今日はここまでです。ありがとうございました。
Newton力学編 目次
① 力学とは何か
② 位置の表し方 ←今ココ!
③ 運動エネルギーと運動量
④ 運動の三法則
⑤ 種々の力
⑥ 仕事と力積
⑦ 運動方程式を解く
⑧ 回転運動
⑨ 剛体の運動
⑩ 反発係数
◼︎ 章末問題
