
ロードバイクの速度の気温変化を調べてみた
こんにちは
ロードパーツが大好きなSilicate meltと申します。
1年前にパワーメーターを導入したワタクシ
これまでにいろいろな試験をしてきたのですけれども、まだ調べ切れていなかったのが、気温と速度の関係でした。
冬にロードバイクに乗ると、夏と比べて速度が出にくいわけですけれども、具体的にどれくらい速度が変わるのか?
これを知りたいと思っていました。
速度が季節で変わるのは、空気の密度が気温変化することがその理由で、ネットで検索をするとその解説や実測データを報告しているサイトが多く見つかります。
でもね…
<例1> ふじいのりあき氏「35km/hで走るために、夏は188Wでいいけど、冬は204W必要だった」
<例2> Y氏「210Wで走ったら、夏は32km/h出たけど、冬は29km/hしか出なかった」
<例3> FF-Cycle氏「1周10kmのトレーニングコースを240W前後で走ったら、気温27℃では36km/hで走れたけど、気温8.8℃では34.7km/hしか出なかった」
とか、そんな感じ(他にも似たような報告多数)。
インターネット上で、ロードバイクの速度に対する気温の影響について書いているサイトの情報は、どれもこれも
速度域が高いのです!
自慢じゃないけど、僕はそんな速度は出せません。
(だって、FTP 170Wくらいしかないから… ・゚・(ノД`)・゚・。)
僕はロングライドが好きなのですけれども、いつもだいたい140W前後、メーター読み28〜25km/hくらいで走っています。
これくらいのパワーと速度域での、気温と速度の関係が知りたいのです!!
実際、リアルなサイクリングってそんな感じなのではないでしょうか?
(ソロで時速35kmで200km走れる人なんて、なかなかいないです)
このnoteでは、そんな
多くのサイクリスト諸氏にとってのリアルな速度域での、気温と速度の関係について考えてみました。
1.理論式からの推察
多くのサイトで解説されているように、気温が低くなるとロードバイクの速度が遅くなるのは、主に
(1)気温が低いほど空気の密度が高くなり空気抵抗が大きくなる
(2)気温が低いときにはウエアの空気抵抗が大きくなりやすい
ことによるものです。
空気抵抗力$${F}$$は、空気の密度$${ρ}$$、空気抵抗係数$${Cd}$$、前面投影面積$${A}$$、走行速度$${v}$$を用いて、
$$
F=\frac{1}{2}ρCdAv^2
$$
空気抵抗力に打ち勝つための仕事率$${P}$$は$${F}$$と$${v}$$の積であり、
$$
P=\frac{1}{2}ρCdAv^3
$$
と表されます。
ここで$${A}$$は身長と体重からの推算式があって、自分の場合は0.41になります。また$${Cd}$$はロードレーサーは0.88、トラック競技の場合は0.70位だそうです(いずれも、ソースはCBN blog、 GleenGould氏のRoadLoadSurveyor_manual_4th_editionによる。しかし、最近リンクが消えてしまったらしい)。$${ρ}$$は温度の関数で、ネット上にいろいろな計算機があります(例えばコレとか)。
上式とこれらの数値を使うと、速度とパワーと温度の関係は下図のようになります。

空気抵抗に打ち勝つためのパワー($${P}$$)は速度の3乗に比例する。
速度が低いときほど$${P}$$に与える温度の影響は小さくなります。
時速20-30kmの速度域の拡大図が下です。

時速20-30kmの速度域の拡大図
時速25kmくらいの速度域において、気温が30℃から0℃まで低下すると、速度が約1km/h低下するらしいです。

冬は重ね着をしたりしてウエアのピチピチ度が低下しますから、空気抵抗係数$${Cd}$$が大きくなりそうです。具体的な数値はよくわからないのですが、(ロードが0.88、ピストが0.70という数値を参考に類推して)仮に冬用ウエアで$${Cd}$$=1.00としてみると、上図の結果になります。
気温0℃で冬用ウエアを着て走ると、気温30℃で夏用ウエアを着て走るよりも速度が2km/hくらい低下しそうなことがわかります。
つまり、夏と比較した時の冬の速度低下は、空気密度の寄与とウエアの寄与がほぼ50%づつくらいであると推測されます。
この、夏と冬の速度の違いが定量的に妥当なものであるのかどうかを実際に計測して確かめてみました。
2.パワーメーター試験
2-1 試験の方法
自転車(その1): LOOK565、Continental GP5000 25C クリンチャー(7気圧)、重量7.9kg
自転車(その2):Nationalレーサー、Vittoria Strada 21-28 チューブラー(7気圧)、重量9.3kg
試験地(A):秋田市向浜のココ
1.5km先が行き止まりになっている南北の平坦路で、東西に防風林があるため、風を受けにくい場所です。ただし舗装路面が傷んでいるところが多い。
試験地(B):秋田市向浜のココ
試験地 Aの一本東の産業道路です。試験地 Aと比べると路面が良い場所で、舗装路としては普通。ここは舗装路面の状態の違いによる計測結果の違いを確認するために、Nationalレーサーのみで試験しました。
走行条件:ポジションは下ハン、ギヤ比2.6くらい
記録:パワーメーター(Garmin RK100)による3秒平均パワーをGarmin Edge840で記録
100W、140W、180W目安で一定となるように往復する。
終了後に1秒間隔で記録されたログを取得し、片道1.5kmのうち速度が安定してくる後半1kmの部分の速度とパワーの平均値を求める。さらに行きと帰りの平均を求める。
気象条件:気温2〜4℃、東〜東南東の風 1.5〜2.5m/s
気温は気象台(試験地Aから3kmくらいの場所)で記録された試験時刻(10分ごと)の値を参照。ちなみに、Garmin Edgeにも温度計が内蔵されていますが、経験的に誤差が大きいような気がします。
ウエア:
写真のやつと同じものを着用しています。
上:ワークマンで買ったやつ
下:Funkierの冬用ビブタイツ

2-2 試験の様子
珍しく晴れた2月のとある休日
これは "冬季パワーメーター試験の絶好のチャンス" とばかりに、
LOOK565に乗って試験地Aに行きました。
実は当日、市内中心部は道路にも雪が結構残っておりまして、
「試験地は除雪もしてないだろうし、無理かなぁ」
と思いつつ、ダメ元で行ってみたのですが、逆に沿岸は市内と違って雪がほとんどありませんでした。
(数キロしか離れていないのに不思議だ)


100W→140W→180W→100W→140W→180W の順に2回ずつ往復しました。
一旦帰宅してNationalレーサーに乗り換えます。


同様に、100W→140W→180W→100W→140W→180W の順に2回ずつ往復しました。
試験が終わったころ、上空から鳥の鳴き声が…


渡り鳥がV字飛行をしていました。
後ろの鳥は前の鳥の羽ばたきによる上昇気流を受けるため、集団で平均するとかなりの省エネルギーで飛ぶことができるそうです。
しかも、1羽もサボることなく全員でちゃんと先頭交代をしているのだとか。
ロードバイクとそっくりですね(笑)

こちらは試験地Bです。
Nationalレーサーで片道1.5kmを100W→140W→180Wの順に往復しました。
2-3 試験の結果
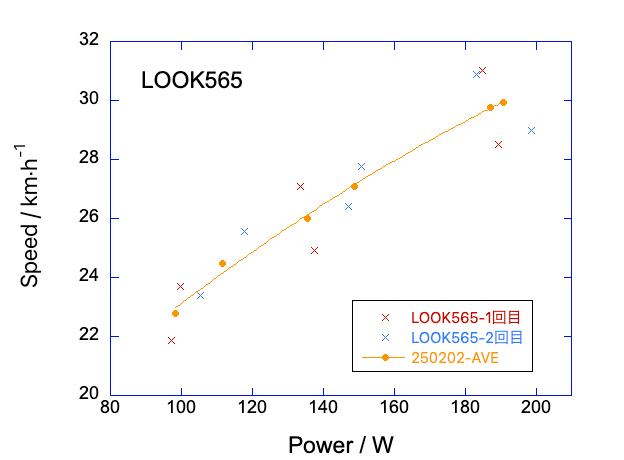
LOOK565の結果を図6-4に示します。
ここは防風林があるので、もともと風の影響を受けにく場所なのですが、それでもわずかに風があるので、同じパワーでも「行き」と「帰り」では速度が変わってしまいます。ところが、それらを平均した上で2回の計測をプロットすると、一本の曲線に乗ることがわかります。
このことは、行きと帰りを平均化して"無風換算"の値とすることで、再現性の高い計測ができていることを示しています。
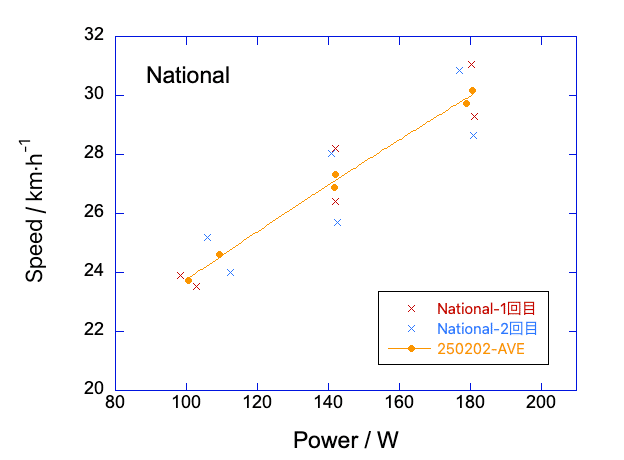
Nationalレーサーの結果を図6-5に示します。
2回の計測で再現性があることが確かめられました。

試験地AとBの比較を図6-6に示します。
舗装路面の状態が良い試験地Bの方が0〜0.4kmhほど速い結果となりました。
3.考察
試験地Aでは昨年6月22日と8月25日にも計測をしておりまして、その結果は以前noteに書きました。
2024年6月22日計測↓
2024年8月25日計測↓

試験地A、空気圧7bar、
白抜きシンボル:LOOK565、
塗りつぶしシンボル:Nationalレーサー
夏に行った過去2回の結果と今回の結果の比較を図6-7に示します。
さらに、図6-7の速度をパワーの二次関数で近似し、100W、140W、180Wでの速度と計測時の気温の関係をプロットしたものを図6-8に示します。

試験地A、空気圧7bar、
白抜きシンボル:LOOK565、
塗りつぶしシンボル:Nationalレーサー
図6-7と図6-8から次のことが分かる。
(1)パワーが一定のとき、8月>6月>2月の順で速度が速くなる。気温が30℃下がると速度を保つために必要なパワーが約35W増加する。つまり、気温が1℃変わると速度を保つためのパワーは1.2W変わる。
(2)100W、140W、180Wのいずれも、気温が30℃下がると速度が3km/h下がる。つまり、気温が1℃変わると速度は0.1km/h変わる。
(3)180Wでは気温25-33℃の範囲で速度に差が生じない。
(4)夏はNationalレーサーよりもLOOK565の方が速いが、冬はLOOKよりもNationalレーサーの方が速い
<考察 その1> 本計測と既報の報告との違いについて
(1)と(2)は既報の報告と比べて明らかに大きな値です。
このnoteの最初に紹介したように、ふじい氏は35km/hにおいて、夏と冬で16Wしか違いがないと述べていました。
ところが、ワタクシの計測では24-32km/hの比較的遅い速度域でさえ、夏と冬では35Wもの差が生じていることが判明しました。
また、FF-Cycle氏は240W前後のほぼ一定のパワーで走行したとき、夏と冬では1.3km/hの速度差しか生じないと述べていました。
ところが、ワタクシの計測では24-32km/hの比較的遅い速度域でさえ、一定パワーでは夏と冬で約3km/hもの速度差が生じていることが判明しました。
なぜこのような食い違い生じたのか?
そもそもなのですけれども、ふじい氏やFF-Cycle氏が報告した「夏と冬の違い」は図6-1に示した単純な試算よりもずいぶん小さいように見えます。
ワタクシの計測は平地の直線を往復することで無風換算の値を算出しています。一方、ふじい氏やFF-Cycle氏の値はロードトレーニングでの値なだけで、このような計測をするために注意深く走行したわけではありません。
ふじい氏やFF-Cycle氏の計測では風の影響が一定ではなかったのかもしれません(図6-4に示したように、弱い風でも2km/h位は平気で変わります)
他の可能性としては、私のウエアの空気抵抗が他の方々よりも大き過ぎたことも考えられます。
<考察 その2> ロングライドでの計測結果と比べてみる
今回のパワーメーター試験の結果は、実際のロングライド走行時の気温差と速度差の関係ともほぼ一致することがわかりました。
以前、ロングライドのパワーメーター試験を行ったことがあるのですが(下記note)、210kmのコースを気温5.7℃で走行したときネット平均速度は22.7km/hであったのに対し、気温30.1℃では25.2km/hでした。24.4℃の気温差で2.5km/hの速度差ですから、(2)の事実(気温が1℃変わると速度は0.1km/h変わる)とよく一致しています。
<考察 その3> カーボンバイク(クリンチャー)とクロモリレーサー(チューブラー)の違いについて
今回のもうひとつの新発見は(4)の 冬はLOOKよりもNationalレーサーの方が速い という事実です。
100Wから180Wの範囲で常にそのようですから、これは十分に再現性のある現象です。この2台のマシンの空力抵抗はあまり変わらないと思うので、これはタイヤの差に由来するものと思われます。
夏に計測したときはNationalの方が0.3km/hほど遅く、これはチューブラー(Vittoria STRADA)の転がり抵抗が大きいためだと考えていました。
ところが冬に計測すると、なんと逆の結果
チューブラーの方が0.5km/hほど速かった!
転がり抵抗に温度依存性があり、クリンチャー(Continental GP5000)は冬は不利になるということなのだろうか??
いずれにせよ、夏と冬で1年を通せばカーボンバイクとクロモリレーサーの速度差は平均化されることになります。
つまり、チューブラーのクロモリレーサーはクリンチャーのカーボンバイクと遜色のない走りをする、ということ。
クロモリは「遅い」とか「のんびり走る ゆるポタにピッタリ」とか言われているけれども、マシンの本質的な性能としてはぜんぜんそんなことはなくて、クロモリだって速いのです!
遅いのは、乗り手にパワーがないだけの話ってことだわな ・゚・(ノД`)・゚・。
「クロモリは遅い」なんて意見は、自分の貧脚を棚に上げて、責任転嫁をしているに過ぎないのだ!!
4.まとめ
ロードバイクによる一般的なサイクリングでの速度域(100W〜180W、24〜32km/h)でのパワーと速度、気温の関係を計測したところ、次のことが判明した。
(1)気温が30℃下がると速度を保つために必要なパワーが約35W増加する。つまり、気温が1℃変わると速度を保つためのパワーは1.2W変わる。
(2)パワーが一定のとき、気温が30℃下がると速度が3km/h下がる。つまり、気温が1℃変わると速度は0.1km/h変わる。
(3)(1)と(2)の大きさは、実際のロングライド走行で記録された速度と気温の関係とも定量的によく一致する。
(4)(1)と(2)の大きさは、空気密度の温度依存性だけでは説明がつかず、ウエアの空気抵抗やタイヤの転がり抵抗の温度変化なども大きく影響していそうである。
(5)チューブラーのクロモリレーサーは速い!
僕のウエアは冬用としては標準的なスタイルに思うのですが、もう少し工夫をして空気抵抗を低減させれば速度アップにつながりそうなので、考えてみたくなりました。
あと、今回一番の驚きは(5)の事実なのですけれども、別の場所でも追試をして確かめてみたいところです。
図6-8を使えば、パワーメーターを持っていない人でも、自分が普段トレーニングをしているコースの複数回の平均速度とその時の気温から、自分のパワーを知ることができます。気温変化に比べるとバイクの違いや舗装路面の違いの影響はずっと小さいので、図6-8の関係は割と普遍的に成り立ちそうです。
(終わり)
