
Ologで再起関数の例:フィボナッチ数
下記のExample 6.6.1のOlogが面白かったので、フィボナッチ数を求める再帰関数でもやってみた。
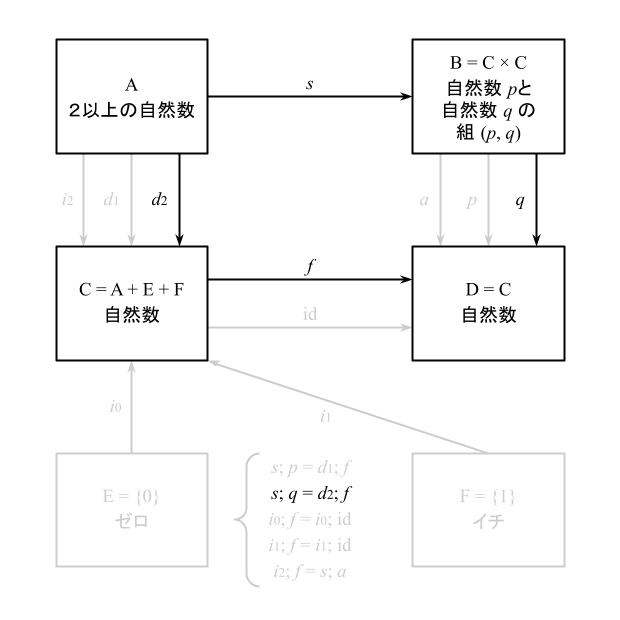
フィボナッチ数のOlog
次のように描いた(直和の記号$${\amalg}$$が面倒だったので、+で代替している)。

二つ組
射影 $${p, q}$$の性質から、 $${s}$$がどのような二つ組を作るかわかる。
$${s(n) = (f(d_1(n)), f(d_2(n)))}$$
したがって、$${f(i_2(n)) = a(s(n)) = a(f(d_1(n)), f(d_2(n)))}$$になる。

場合分け
恒等写像の性質から$${\text{id}(0) = 0, \text{id}(1) = 1}$$となる。これと、直和に伴う包含写像 $${i_0, i_1, i_2}$$の性質から、$${f}$$は次のように場合分けで書ける。
$$
f(n) = \left\{ \begin{array}{ll}
0 & \text{if} n = 0\\
1 & \text{if} n = 1 \\
a(f(d_1(n)), f(d_2(n))) & \text{if} n \gt 1
\end{array} \right.
$$



残りの関数の選定
$${a, d_1, d_2}$$を次のような関数とすれば、$${f(i_2(n)) = f(n - 1) + f(n - 2)}$$となる。
$${a(x, y) = x + y}$$:和
$${d_1(n) = n - 1}$$:前者関数
$${d_2(n) = n - 2}$$:前々者関数
すると、$${f}$$は次のように書けて、確かにフィボナッチ数の再帰関数になる。
$$
f(n) = \left\{ \begin{array}{ll}
0 & \text{if} n = 0\\
1 & \text{if} n = 1 \\
f(n - 1) + f(n - 2) & \text{if} n \gt 1
\end{array} \right.
$$
