
雀の圏(じゃんのけん、英: category of sparrows)
日曜数学 Advent Calendar 2022の12月6日用の記事として、この記事を作成した。
ちなみに、私の知る限り数学に雀(じゃん)なんて概念はない。じゃんけんに引っ掛けてダジャレを言いたいがためにテキトーにでっち上げた概念である。
もしかすると私が知らないだけで、雀には興味深い性質があるかもしれない。しかし、少なくともこの記事では単なるオモチャだ。ガチャガチャいじって遊ぶだけで、とくに証明もしない。肩の力を抜いて読んで欲しい。
もしも日曜数学 Advent Calendar的にこの記事がNGだったら、近所のすずめにパンなどの食材を贖罪として捧げてこようと思う。
雀の定義
反射律と反対称律を満たす二項関係を雀(じゃん、英: sparrow)と定義する。すなわち雀$${(J, \preceq)}$$において、台集合$${J}$$上の二項関係$${\preceq}$$は次の条件を満たす。
反射律:任意の$${x \in J}$$について、$${x \preceq x}$$
反対称律:任意の$${x, y \in J}$$について、$${x \preceq y}$$かつ$${y \preceq x}$$ならば$${x = y}$$
異なる2つの元同士で関係が成り立つとき、すなわち$${x \ne y}$$かつ$${x \preceq y}$$が成り立つとき、$${x \prec y}$$と書いて、$${x}$$は$${y}$$に負ける、あるいは$${y}$$は$${x}$$に勝つと言う。
$${x}$$と$${y}$$が互いに勝ちも負けもしないとき、すなわち$${x \preceq y}$$と$${y \preceq x}$$のどちらも成り立たないか、$${x = y}$$のとき、$${x \sim y}$$と書いて、$${x}$$と$${y}$$はあいこであると言う。
記法の乱用として、雀$${(J, \preceq)}$$を$${J}$$と書く。また、$${J}$$上の二項関係であることを意識する場合、$${\preceq}$$を$${\preceq_J}$$と書くこともある。
この定義を考えた背景
じゃんけんに引っかけて雀を定義したいので、二つの手に対して勝ち、負け、あいこの3パターンが定義できるような構造が欲しかった。なんの制約もない二項関係Rは、二つの手x, yに対して¬xRy∧¬yRx, ¬xRy∧yRx, xRy∧¬yRx, xRy∧yRxの4パターンがあり得る。1パターン多い。勝ち負けの反対称性とあいこの対称性を考えると、完全律か反対称律のどちらか一方を採用するのが良さそうに思える。ただ、完全律には全順序の直積順序が半順序になってしまうような難しさがあった。そのため、反対称律を採用することにした。そして準同型が考えやすくなるように反射律も採用した。
雀の例

じゃんけんは雀である。
石(グー)、鋏(チョキ)、紙(パー)の関係をすべて書き下すと、$${_石 \preceq {}_石}$$, $${_鋏 \preceq {}_鋏}$$, $${_紙 \preceq {}_紙}$$, $${_石 \preceq {}_紙}$$, $${_紙 \preceq {}_鋏}$$, $${_鋏 \preceq {}_石}$$となる。
関係を詳細に見れば、$${_石 \sim {}_石}$$, $${_鋏 \sim {}_鋏}$$, $${_紙 \sim {}_紙}$$が成り立っている。また、$${_石 \prec {}_紙}$$, $${_紙 \prec {}_鋏}$$, $${_鋏 \prec {}_石}$$である。言い換えれば、石と石、鋏と鋏、紙と紙はあいこで、石は紙に、紙は鋏に、鋏は石に負ける。
集合$${\{0, 1\}}$$の大小関係$${\leq}$$は雀である。関係を書き下せば$${0 \leq 0}$$, $${0 \leq 1}$$, $${1 \leq 1}$$であって、反射律と反対称律を満たす(より一般に、全順序関係の完全律を忘れれば半順序関係とみなせるし、半順序関係の推移律を忘れれば雀とみなせる)。
$${\preceq}$$を矢印(→)にして図示すると雀が捉えやすくなるかもしれない。
雀の準同型写像
2つの雀$${I}$$, $${J}$$の間の雀準同型写像$${f: I \to J}$$とは、任意の$${x, y \in I}$$について$${x \preceq_I y}$$ならば$${f(x) \preceq_J f(y)}$$が成り立つ写像である。
任意の雀$${J}$$の台集合上の恒等写像$${\text{id}: J \to J}$$は雀準同型写像である。なぜなら、すべての$${x, y \in J}$$について、$${x \preceq y}$$ならば$${\text{id}(x) = x \preceq y = \text{id}(y)}$$が成り立つ。
任意の3つの雀$${I, J, K}$$と、任意の2つの雀準同型写像$${f: I \to J}$$, $${g: J \to K}$$が与えられたとする。このとき、合成写像$${g \circ f: I \to K}$$は、$${I}$$と$${K}$$の間の雀準同型写像になる。なぜなら$${f}$$が雀準同型写像なので、任意の$${x, y \in I}$$について$${x \preceq_I y}$$ならば$${f(x) \preceq_J f(y)}$$が成り立ち、$${g}$$が雀準同型写像なので、$${f(x) \preceq_J f(y)}$$から、$${g \circ f (x) = g(f(x)) \preceq_K g(f(y)) = g \circ f (y)}$$が成り立つ。

中段:{p, q, r, s}から{石, 鋏, 紙}への全射だが単射でない雀準同型写。
像下段:{0, 1}から{2, 3}への全単射な雀準同型写像(同型)。

中段:{0', 1'}から{0, 1}への全単射な雀準同型写像(同型ではない)。
下段:{p, q, r, s}から{a', b', c', d', e', f'}への全射でも単射でもない雀準同型写像。
雀の圏
雀の圏Sprwは、雀を対象とし、雀準同型写像を射、写像の合成を射の合成とした圏である。これが本当に圏になっているかは確かめない。
ところで集合の圏Setは集合を対象とし、写像を射、写像の合成を射の合成とした圏である。集合の圏では、恒等写像が単位射として単位律を満たし、写像の合成が結合律を満たしている。
恒等写像が雀準同型写像であること、雀準同型写像の合成が再び雀準同型写像になることは既に確かめてある。つまり、集合の圏Setを圏であると認めるなら、雀の圏Sprwも圏と認められるだろう。
雀の圏の中
雀の圏Sprwは作れたので、やりたいことはできた。おまけでSprwの中を少しだけ覗いておこう。ここまでしてこなかったが、以降も定義と証明は適宜省略する。
始対象
空集合上の空関係は雀であり、空写像は雀準同型写像になる。これらは圏Sprwの始対象である。

終対象
任意の単元集合$${T}$$には元$${t \in T}$$がただ一つしか存在しない。等号$${t = t}$$は反射律と反対称律を満たすので、単元集合と等号は雀である。始域のすべての元を単元集合のただ一つの元へ写す定値写像は雀準同型写像になる。これらは圏Sprwの終対象である。

積
雀$${I, J}$$の直積集合からなる雀を、直積雀と呼ぶ。ただし、直積雀$${I \times J}$$の二項関係は任意の$${(x, y), (x', y') \in I \times J}$$について、$${x \preceq y \land x' \preceq y' \iff (x, x') \preceq (y, y')}$$と定義される。また、射影$${\pi_1: I \times J \to I, \pi_2: I \times J \to J}$$はどちらも雀準同型写像になる。直積雀と射影は圏Sprwの積である。

【注】自己ループは省略している
余積
雀$${I, J}$$の直和集合からなる雀を、直和雀と呼ぶ。ただし、直和雀$${I + J}$$の二項関係は任意の$${x, y \in I + J}$$について、$${x \preceq_I y \lor x \preceq_J y \iff x \preceq_{I + J} y}$$と定義される。また、包含写像$${\iota_1: I \to I + J, \iota_2: J \to I + J}$$はどちらも雀準同型写像になる。直和雀と包含写像は圏Sprwの余積である。

【注】自己ループは省略している
等化子
雀$${I, J}$$と雀準同型写像$${f, g: I \to J}$$から定まる雀$${\text{Eq}(f, g)}$$を等化子と呼ぶ。ただし、等化子の台集合は$${\{ x \in I \mid f(x) = g(x)\}}$$で定義される。また、等化子の二項関係は任意の$${x, y \in \text{Eq}(f, g)}$$について、$${x \preceq_I y \iff x \preceq_{\text{Eq}(f, g)} y}$$と定義される。また、包含写像$${\iota: \text{Eq}(f, g) \to I}$$は雀準同型写像になる。等化子と包含写像は圏Sprwの等化子である。

【注】自己ループは省略している
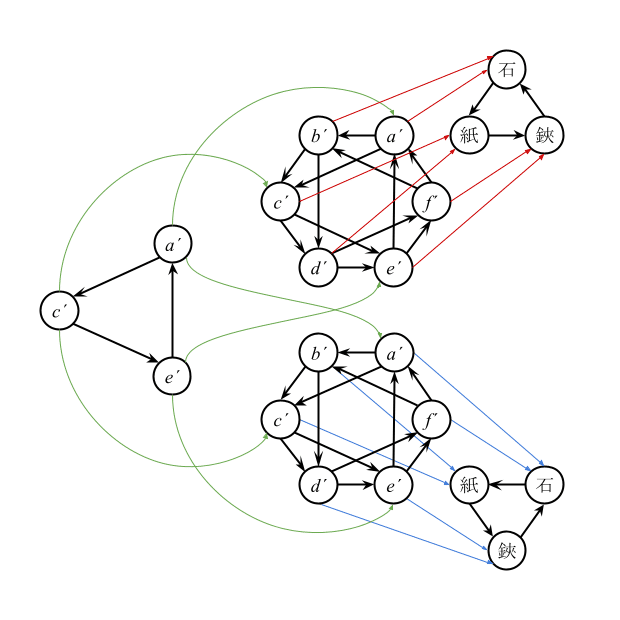
【注】自己ループは省略している
余等化子
雀$${I, J}$$と雀準同型写像$${f, g: I \to J}$$から定まる雀$${\text{Coeq}(f, g)}$$を余等化子と呼ぶ。ただし、余等化子の台集合は、同値関係$${\approx}$$で$${J}$$を割った商集合$${\text{Coeq}(f, g) = J /_{\approx}}$$として定義される。ここで、同値関係$${\approx}$$は、任意の$${x \in I}$$について、$${f(x) \approx g(x)}$$であり、任意の$${x, y, z, w \in J}$$について、$${x \preceq y \land y \approx z \land z \preceq w \land w \approx x}$$ならば$${x \approx y \approx z \approx w}$$と定義する。また、余等化子の二項関係は任意の$${[x], [y] \in \text{Coeq}(f, g)}$$について、$${x \preceq y}$$を満たす$${x \in [x], y \in [y]}$$が存在するとき、かつその時に限り$${[x] \preceq [y]}$$と定義される。また、商写像$${\pi: J \to J /_{\approx}}$$は雀準同型写像になる。余等化子と商写像は圏Sprwの余等化子である。
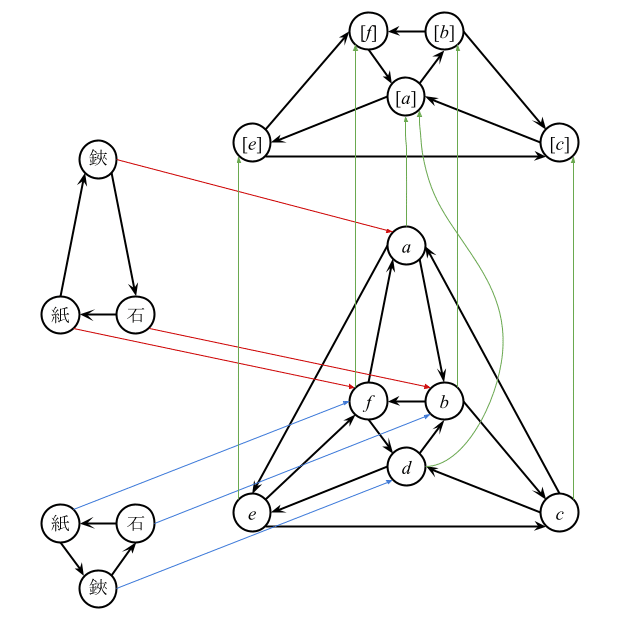
【注】自己ループは省略している

【注】自己ループは省略している
引き戻し
雀$${I, J, K}$$と雀準同型写像$${f: I \to K, g: J \to K}$$から定まる雀$${I \times_K J}$$を引き戻しと呼ぶ。ただし、引き戻しの台集合は$${\{ (x, y) \in I \times J \mid f(x) = g(y)\}}$$で定義される。また、引き戻しの二項関係は任意の$${(x, y), (x', y') \in I \times_K J}$$について、$${x \preceq y \land x' \preceq y' \iff (x, x') \preceq (y, y')}$$と定義される。また、制限された射影$${\pi_1: I \times_K J \to I, \pi_2: I \times_K J \to J}$$はどちらも雀準同型写像になる。引き戻しと制限された射影は圏Sprwの引き戻しである。

【注】自己ループは省略している
押し出し
雀$${I, J, K}$$と雀準同型写像$${f: K \to I, g: K \to J}$$から定まる雀$${I +_K J}$$を押し出しと呼ぶ。ただし、押し出しの台集合は、同値関係$${\approx}$$で$${I + J}$$を割った商集合$${I +_K J = (I + J) /_{\approx}}$$として定義される。ここで、同値関係$${\approx}$$は、任意の$${x \in K}$$について、$${f(x) \approx g(x)}$$であり、任意の$${x, y, z, w \in J}$$について、$${x \preceq y \land y \approx z \land z \preceq w \land w \approx x}$$ならば$${x \approx y \approx z \approx w}$$とする。また、押し出しの二項関係は任意の$${[x], [y] \in I +_K J}$$について、$${x \preceq_I y \lor x \preceq_J y}$$を満たす$${x \in [x], y \in [y]}$$が存在するとき、かつその時に限り$${[x] \preceq_{I +_K J} [y]}$$と定義される。なお、包含写像$${\iota_1: I \to I + J, \iota_2: J \to I + J}$$と商写像$${\pi: I + J \to I +_K J}$$の合成写像$${\pi \circ \iota_1, \pi \circ \iota_2}$$はどちらも雀準同型写像になる。押し出しと上記の合成写像は圏Sprwの押し出しである。

【注】自己ループは省略している

【注】自己ループは省略している
雀の圏の外
Sprwと外の関係も少しだけ覗いておこう。
Sprw→Set
雀の圏Sprwから集合の圏Setへの関手の例をあげる。この関手は二項関係を忘れて、雀の台集合をそのまま集合へ写す。雀準同型写像は写像なので、そのまま写像へ写る。

Set→Sprw
集合の圏Setから雀の圏Sprwへの関手の例をあげる。この関手は集合を元の等号関係のをみを入れた雀に写す。つまり集合$${J}$$を、任意の$${x, y \in J}$$について$${x = y \iff x \preceq y}$$と定義される二項関係を持った雀に写す。このような雀を離散雀と呼ぶ。任意の写像は、離散雀から離散雀への雀準同型写像とみなせる。

Sprw→Grph
雀の圏Sprwから有向グラフの圏Grphへの関手の例をあげる。この関手は雀の台集合をグラフの頂点集合に写し、二項関係を有向辺に写す。つまり$${x \preceq y}$$のとき、かつその時に限り$${x \to y}$$となる有向辺が存在する。雀準同型写像はそのままグラフ準同型写像になる。この関手によって写される有向グラフを雀のグラフと呼ぶ。反射律より雀のグラフの各頂点には自己ループがある。また、反対称律より長さ2の閉路は存在しない。そして、二項関係が多重に成り立つことはないので、雀のグラフに多重辺は存在しない。

【注】自己ループは省略している
Grph→Sprw
有向グラフの圏Grphから雀の圏Sprwへの関手の例をあげる。この関手はグラフの頂点集合$${J}$$を同値関係$${\approx}$$で割った商集合$${J/{\approx}}$$へ写す。ここで、同値関係$${\approx}$$は、任意の$${x, y \in J}$$について、$${x \to y, y \to x}$$の2つの有向辺があれば$${x \approx x}$$であり、さらに任意の$${x, y, z, w \in J}$$について、$${x \to y, z \to w}$$なる2つの有向辺があって、$${y \approx z \land w \approx x}$$ならば$${x \approx y \approx z \approx w}$$とする。また、この関手で得られる雀$${J/{\approx}}$$の二項関係は任意の$${[x], [y] \in J/{\approx}}$$について、$${x \in [x], y \in [y]}$$であって、$${x = y}$$または、有向辺$${x \to y, y \to x}$$のいずれかが一つでも存在するとき、かつその時に限り$${x \preceq y}$$と定義される。すべてのグラフ準同型写像$${f: I \to J}$$は、商写像$${\pi_1: I \to I/{\approx}, \pi_2: J \to J/{\approx}}$$を使って、写像$${g: I/{\approx} \to J/{\approx}}$$に写る。$${g}$$は任意の$${x \in I}$$について$${g(\pi_1(x)) = \pi_2(f(x))}$$が成り立ち、$${g}$$は雀準同型写像となるが、確認は省略する。

【注】自己ループは省略している
Poset→Sprw
半順序の圏Posetから雀の圏Sprwへの関手の例をあげる。この関手は推移律を忘れて、半順序を雀とみなす。半順序の同調写像は雀準同型写像へそのまま写る。

【注】自己ループは省略している
Sprw→Poset
雀の圏Sprwから半順序の圏Posetへの関手の例をあげる。この関手は雀$${J}$$の台集合を同値関係$${\approx}$$で割った商集合$${J/{\approx}}$$へ写す。ここで、同値関係$${\approx}$$は$${\preceq_J}$$の反対称律を忘れ、推移律によって拡張された(推移閉包をとった)二項関係$${\preceq'}$$によって定義される。すなわち、$${\preceq'}$$は任意の$${x, y, z \in J}$$について、$${x \preceq z \lor x \preceq' y \land y \preceq' z \iff x \preceq' z }$$と定義される。そして、同値関係$${\approx}$$は任意の$${x, y \in J}$$について、$${x \preceq' y \land y \preceq' x \iff x \approx y}$$と定義される。すべての雀準同型写像$${f: I \to J}$$は、商写像$${\pi_1: I \to I/{\approx}, \pi_2: J \to J/{\approx}}$$を使って、写像$${g: I/{\approx} \to J/{\approx}}$$に写る。$${g}$$は任意の$${x \in I}$$について$${g(\pi_1(x)) = \pi_2(f(x))}$$が成り立ち、$${g}$$は半順序の同調写像となるが、確認は省略する。
有向グラフを強連結成分分解することで、DAG(有向非巡回グラフ)が得られる。半順序のグラフはDAGである。雀のグラフを強連結成分分解して、雀のグラフ上の到達可能性を考えると半順序が得られる。この関手はそのように理解できる。

【注】自己ループは省略している
敗射と勝射
Sprwの終対象$${T}$$から離散雀$${D}$$への任意の射$${p}$$を参加射(player)と呼ぶ。離散雀$${D}$$から任意の雀$${J}$$への任意の射$${g: D \to J}$$をゲーム(game)と呼ぶ。押し出し$${J +_D J}$$を考えると、射$${\iota_1, \iota_2: J \to J +_D J}$$が得られる。さらに等化子$${\text{Eq}(\iota_1, \iota_2)}$$を考えると、射$${\iota: \text{Eq}(\iota_1, \iota_2) \to J}$$が得られる。等化子の普遍性から$${g = \iota \circ r_g}$$となる射$${r_g: D \to \text{Eq}(\iota_1, \iota_2)}$$が一意に存在し、$${r_g}$$をゲーム$${g}$$のリプレイ(replay)と呼ぶ。そして、等化子$${\text{Eq}(\iota_1, \iota_2)}$$から雀$${(\{0, 1\}, \le)}$$へのエピ射をゲームの審判(umpire)と呼ぶ。最後に、終対象$${T}$$の唯一の元を$${(\{0, 1\}, \le)}$$の$${0}$$へ写す射を判定(judgment)と呼ぶ。
参加射$${p}$$、リプレイ$${r_g}$$、判定$${j}$$について、$${j = u \circ r_g \circ p}$$となる審判$${u}$$が存在すれば、参加射$${p}$$をゲーム$${g}$$の敗射(loser)と呼ぶ。また、そのような$${u}$$が一つも存在しない場合、参加射$${p}$$をゲーム$${g}$$の勝射(winner)と呼ぶ。すべての参加射が敗射であるか、すべての参加射が勝射であるとき、ゲームは引き分けであると言う。

q; r_g; u ≠ j
【注】自己ループは省略している
この定義を考えた背景
上記の押し出しと等化子は、Jの誘導部分グラフを得るための操作にあたる。誘導に使われる頂点の集合は圏Setに送られたゲームの像だ。上記では省略しているが、そのように作った誘導部分グラフを強連結成分分解して半順序の圏Posetに送ることを裏では考えている。送った先の半順序に最大元が存在する場合、どのようなトポロジカルソートをして全順序を得ても、最大元は最大元にしか写れない。つまるところ、審判がエピ射である限り、最大元にしか写れない射を勝射として思い描いている。
おわり
こんな感じのおふざけを、コテンラジオのレヴィ=ストロースの回を聴きながら考えていた。
