
データ構造とアルゴリズム | ④二分探索木(1)
こんにちは、現役理系大学生のShogoです!
第4回の内容は、「二分探索木」です。
「二分探索木」の内容は少し長くなっていますので、何回かに分けて説明していこうと思います。今回は、「二分探索木」と「挿入insert()」を主に説明していきます。
二分探索木は、Binary Search Treeともいわれ、データ構造とアルゴリズムを学ぶ上では必須事項となってきます。
しっかりとここで知識をつけておくようにしましょう!
4-1 二分木とは

今回の内容は、二分探索木ですが、そもそもその根幹となる二分木とはどういうものなのでしょうか。
二分木とは、読んで字の如く、2つに分かれる木のデータ構造(木構造)のことをいいます。木構造という名前は、ひっくり返すと木のような構造をしていることが由来です。
例えば、上図のようなものをいいます。このとき「○」を節(ノード)、「ー」を枝といいます。節の一番上を根(ルート)といいます。また、節に対して、1つ下にある節を子、1つ上にある節を親といいます。
二分木にはルールがあり、1つの節に対して、2つ以下の子を持つような木構造となっていなければなりません。つまり、1つの節から3本の枝が出ることは許されないのです。
4-2 二分探索木とは
二分木を踏まえた上で、二分探索木をみていきましょう!
二分探索木とは、左側の節の値が親の値より小さく、右側の節の値が親の値より大きい二分木のことをいいます。
例えばこんな感じです。

上の3つの節をみてみましょう。
親が5、子が3と8となっています。このとき、上記のルールに従うと、「左側の節の値(3)が親の値(5)より小さく、右側の節(8)の値が親の値(5)より大きい」というのを満たしています。
1,3,4と6,8,9でも同様のことが言えると思います。
✅二分木を用いて探索
この二分木を用いて探索を行います。
例えば、先程あげた図で特定の値(6)を探すとしましょう。

根(ルート)は「5」です。「6」は「5」よりも大きいので、右側の節に移動します。次の親は、「8」。「6」は「8」よりも小さいので左側の節に移動します。すると、目的の値「6」に到達することができました。
このように、二分探索木を用いることで、[1, 3, 4, 5, 6, 8, 9]という数字から素早く特定の値を見つけることができました。
つまり、1回探索を行うたびに、探索する対象が半分になる。これが二分探索木のメリットです。
4-3 データの挿入
ここからはコードを用いて解説していきます。
まずはじめは、データの挿入です。
最初に「__init__」を使い、Nodeクラスの初期値を設定していきます。
class Node(object):
def __init__(self, data: int):
self.data = data
self.left = None
self.right = None今回は、「__init__」の引数を「data: int」とし、整数だけを扱うものとします。
引数として受け取った「data」を「self.data」に代入して、自分自身で値を持つようにします。そして、「self.left」「self.right」には初期値として「None」を設定しておきます。
次にデータの挿入(insert)の関数を記述していきます。
def insert(node: Node, data: int):
if node is None:
return Node(data)
if data == node.data:
return node
elif data < node.data:
node.left = insert(node.left, data)
else:
node.right = insert(node.right, data)
return nodeこれは後に実行しながら説明していきます。
✅root = None
class Node(object):
def __init__(self, data: int):
self.data = data
self.left = None
self.right = None
def insert(node: Node, data: int):
if node is None:
return Node(data)
if data == node.data:
return node
elif data < node.data:
node.left = insert(node.left, data)
else:
node.right = insert(node.right, data)
return node
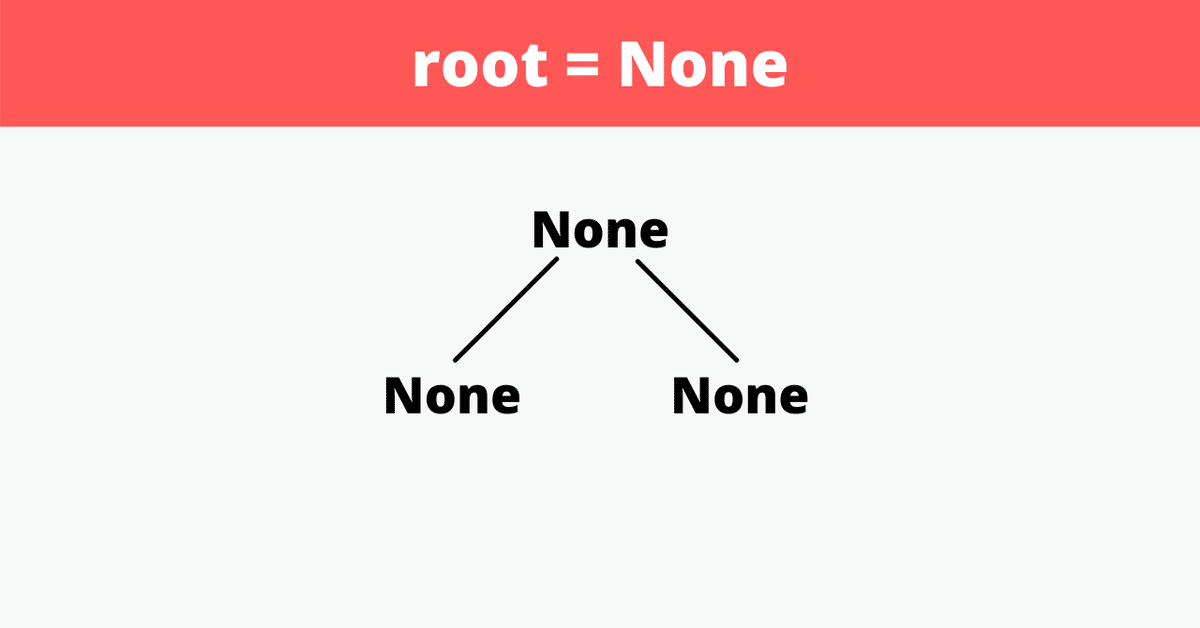
root = None初期設定「__init__」はこのように設定されています。この「None」の節に値を入れていきます。
✅root = insert(root, 5)

class Node(object):
def __init__(self, data: int):
self.data = data
self.left = None
self.right = None
def insert(node: Node, data: int):
if node is None:
return Node(data)
if data == node.data:
return node
elif data < node.data:
node.left = insert(node.left, data)
else:
node.right = insert(node.right, data)
return node
root = None
root = insert(root, 5)
print(root.data)>> 5木の一番上の部分、つまり根の部分に挿入してあげるには、「root = insert(root, 5)」と書きます。ここは少しわかりにくいので、順を追ってい説明します。
「insert(root, 5)」でinsert関数が呼び出される
→「root = None」があるので、「if node is None:」を満たす
→「insert(root, 5)」に「Node(data)」が返される。
→よって『insert(root, 5).data』
→「insert(root, 5)」を「root」に代入し、「root.data」
→これを「print(root.data)」で出力
このような手順を経て、「5」が根(root)に位置するようになります。
✅root = insert(root, 3)

class Node(object):・・・
def insert(node: Node, data: int):・・・
root = None
root = insert(root, 5)
root = insert(root, 3)
print(root.data)
print(root.left.data)>> 5
>> 3続いて「3」を節に挿入します。(Nodeクラス、insert関数のコードを書き続けると、冗長になってしまうので、「・・・」にて割愛しています。)
ここで一旦、二分探索木のルールを思い出しましょう。二分探索木とは、左側の節の値が親の値より小さい二分木のことでした。「3」は「5」よりも小さいため、左の節に挿入されることがわかります。
したがって、次のような流れになります。
「insert(root, 3)」でinsert関数が呼び出される
→「elif data < node.data:」なので、「insert(node.left, data)」
→「node.left」に対して、「insert(node.left, data)」が返した値を入れる
→「node.left」は現時点では「None」
→よって、『insert(None, 3)』で「if node is None:」が実行
→「Node(data)」が『insert(None, 3)』に返され、「node.left」に代入
→「return node」で「root」(根)にもう一度「5」が入る
→「node.left」は「root.left」より「print(root.left.data)」で出力
文章だけじゃわかりにくいと思うので、デバッグしてみるとより一層理解が深まるかと思います。
同様に操作を繰り返すと、下のような二分探索木ができるかと思います。

まとめ

いかがだったでしょうか。
今回は、「二分探索木」の説明と「insert()」についてお話しました。
少し難しかったかもしれませんが、なんども復習して理解するようにしましょう!
この内容は続きものとなっていますので、次回の記事もぜひご覧ください!
質問や訂正があれば、遠慮なくこの記事にコメント、もしくは、TwitterにDMをしてください!(@shogo_python)
今回の記事が"いいね!"と思ってくれた方は、スキとフォローをよろしくおねがいします!
では、またの次の記事でお会いしましょう!
データ構造とアルゴリズム 入門講座 一覧はこちらから
