
Pythonでアルゴリズム「バブルソート」:内側ループで、Range関数の知識が試される件
こんにちは!Pythonで「バブルソート」の続きでございます!😆
前回記事では、バブルソートの「外側のループ」を解説しました。Range関数を上手に使うのがポイントでしたね。
続いて、今回は、「内側のループ」に取り組んでまいります。「内側のループ」は、「右から左へ、隣り合う値を比較して、右の値が小さければ交換」を繰り返します。外側のループにより決定したい値と、その右側を比較したら、「内側のループ」は終了するのでした。
例えば、次の図のような処理をします。

これは、どう書けば実現できるのでしょうか!?今回もRange関数を使いますよ。しかも、「外部ループ」で使うRange関数より、難易度が上がります…😅。でも、これが分かれば、「Range関数マスター」になれちゃうかも!?
準備はいいですか?よし行ってみよ~😄。
一見するだけでは何をしたいのか分からないfor文
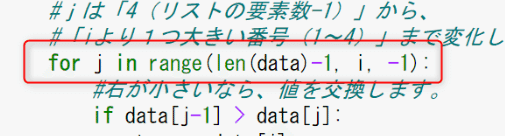
まずは、コードの全体像をもう一度見てみましょう。そして、今回のターゲットは、赤枠内のFor文です。

「Range関数の引数が3つもあって、増分がマイナスすか…😑。今日も、お疲れさまでした!💦」
いや、ちょっと早くないですか!?確かに、何言っているのか、すぐには分からないですね…。でも、まだ帰らないでくださいね~。Range関数の値がどう変化していくのか、きちんと検証しますから😉。
検証:Range関数の値は、どう変化するの?
ではでは、下のFor文を分析します!Range関数が、このFor文の核心です。
カウンタ変数「j」は、Range関数が生成する連番のとおりに変化します。そういえば、Range関数は、連番を得るための関数でしたね。引数が3つあります。このとき、どんな連番が得られるか…。以前、過去記事で紹介しましたが、今一度確認しましょう!
引数が3つのRange関数
引数が3つのRange関数の構文は、次の通りです。
range(start, end, step)
startは、開始値を意味します。Endは終了値を意味します。ただし、「開始値以上、終了値未満」の連番でしたね。Endは、含まれません。
Stepは、「前の数値からいくら増えるか」を表すのでしたね。指定がないなら、「1」なのです。
実際に値の変化を確認!
Range関数の振り返りが済んだところで、今度は実際にカウンタ変数「j」がどう変化するか、確認します!どうやるかって?コードを実行して、jの値を出力してしまいましょうよ😄。
次のようなコードを準備ました。「内側のループ」のコードを、内側のループ範囲の値を出力するコードに書き換えました!実行したら、次の通りです。

「開始値」は、外側のループが何回目であれ、常に「4」で固定です。リストの要素数は、変化しないですからね。その「開始値」は、「要素数ー1」ですね。「要素数ー1」と言えば?そう!リストの最右値の添字でした😄!内側のループは、いつだって「リストの一番右端の値から始まりますよ~」ということなんですね。
「終了値」は、「i未満まで」ということですね。「未満」というと、「その値より小さい」という意味になりますが、今回の場合はちょっと違う。増分がマイナスなので、逆に「iより1段階大きい値まで」ということなります。
例えば、外側1回目のループ(i=0)なら次の通りです。

「iより1段階大きい値」すなわち「1」までループします。これで、指定された範囲の中で、一番小さい値が、0番に移動するというわけです。
あとは、外側のループごとにiの値が小さくなるごとに、内側のループ回数が一つづずへって行き、小さい順に値が並ぶというわけです😅。
読み解けた!?
覚えてますか?交換アルゴリズム
ここまで、分かればもう大丈夫です。これ以降は、もうすでにブログでご紹介した範囲の知識で分かります😆。
下の赤枠のコードは、「右の値が小さいなら、右と左の値を交換してね」と言っているだけです。

見覚え有りません?はい、交換アルゴリズムですよ~。過去記事をぜひぜひ読んでくださいね~。
内側のアルゴリズムの解説で、筆者はエネルギーを使ったので、このIf文の解説は、割愛します~😉。
ということで、バブルソートでございました~。
あ、jの値を書くにするコードを貼っておきますね。
data = [6,9,10,8,5]
#iの値は、0~3まで1ずつ増加します。
for i in range(len(data) - 1):
#jの値がループがどう変わるか出力
j = range(len(data)-1,i, -1)
print("iが",i,"のとき、jは",list(j),"のように変化する。")では、ビーダゼーン!
※私のやる気アップとブログの品質向上につながりますので、記事が気に入られた方は、「ポチっ」と好きボタンを押してくださったり、フォローいただけますと幸いです🙇。
