モンテカルロ法で円周率を求めるのをPythonで実装
Pythonでモンテカルロ法を使って円周率の近似解を求めるというのを機会があってやりましたので、概要と実装について少し解説していきます。
モンテカルロ法とは
モンテカルロ法とは、乱数を用いてシミュレーションや数値計算を行う方法の一つです。大量の乱数を生成して、条件に当てはめていって近似解を求めていきます。
今回は「円周率の近似解」を求めていきます。モンテカルロ法を理解するのに「円周率の近似解」を求めるやり方を知るのが一番有名だそうです。
計算手順
円周率の近似値を求める計算手順を以下に示します。
1. 「1×1」の正方形内にランダムに点を打っていく
(x,y)座標のx,yを、0〜1までの乱数を生成することになります。
2. 「生成した点」と「原点」の距離が1以下なら1ポイント、1より大きいなら0ポイントをカウントします。(円の方程式であるx^2+y^2=1を利用して、x^2+y^2 <= 1なら円の内側としてカウントします)
3. 上記の1,2の操作をN回繰り返します。2で得たポイントをPに加算します。
4. 3で得たポイントPを4倍します(4P)。その後、そのPを乱数を生成した回数であるNで割ります。
4P/Nが円周率の近似値であるπとなります。
π = 4P/N
上記でわかりにくいと思うため、π = 4P/Nで円周率(近似値)が求められる理由を解説していきます。
円周率がなぜ求められるのか
上記の4手順を一つずつ解説していき、円周率が求められる原理について知っていきます。
まず最初に手順1にある「1 x 1」の正方形にx座標,y座標にあたる値を乱数で決定して、点を正方形内に打っていきます。
それぞれの点のx座標,y座標の数値は乱数で決定します。1x1の正方形に内にいくつかの点を打っていくと以下のような感じになります。
点を打つ数であるNはいくつでもかまいませんが、以下の画像の場合は100としています。
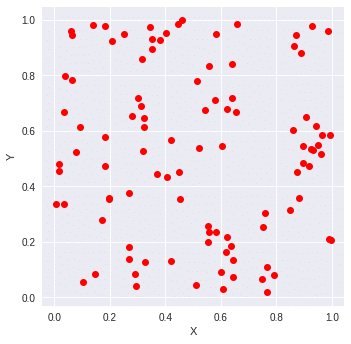
次に上記のそれぞれの点が原点(0,0)から1以下の距離なら1ポイント、限定から(0,0)から1以上の距離なら0ポイントとします。1以下がどうかを判定する式として以下を使用します。
![]()
上記の式は「円の方程式」と呼ばれるものです。以下の画像を見てもらえばわかりますが、単位円(半径が1の円)上で、円より内側を判定する方法としては円の方程式を用います。
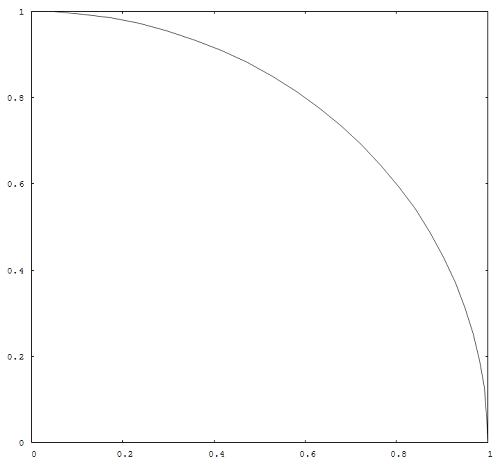
円の内側であるかどうかの判定としては以下の式を用います。つまりはx^2+y^2が1より小さいなら円の内側として判定します
![]()
次に先程の手順で円の内側として判定された点があった場合はPに加算していきます。
そのPを4倍して、最後に乱数を生成した回数であるNで割ればそれが円周率の近似値となります。
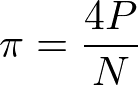
4P/Nで円周率が求められるのはなぜか
4PをNで割った数がなぜ円周率であるπが求まるのかそれを解説していきます。
下記は単位円(半径が1の円)を4分割したものに、ランダムに点を打った画像です。「赤色が円内部の点」、「青色が円外部の点」を表しています。
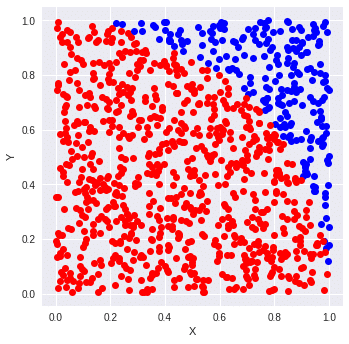
上記の手順3にあるPとは、「円内部である赤色の点」のことです。
つまり、Pを青色と赤色全ての点の数であるNで割ることで、正方形内全体の点の内(N)、円内部にある点の数(P)の割合がわかります。
上記の縦と横が1である正方形のS1の面積は「縦x横」なので、以下の式で求まります。当然縦と横どちらも1なので同じ数を二乗しただけです。
![]()
次に4分割された単位円であるS2の面積を求めます。
円の面積の求め方は「半径 x 半径 x 円周率」なので、以下で求まります。
![]()
4分割された単位円のため、上記で求めた物を4で割ります。これで4分割された単位円の面積であるS2が求まります。
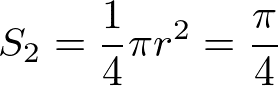
そして上記で求まった「4分割された単位園の面積S2」から「正方形の面積S1」を割ることで、割合がP/Nが求められます。
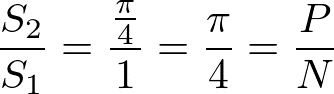
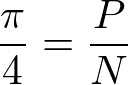
後は上記の式をπで解いてみます。そして以下の用にπ=4P/Nが求められました。
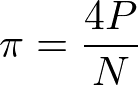
Pythonでのソースコード
それでは上記の長ったらしい式をコードに落とし込みます。至ってシンプルです。Nの値は自由に変えていただいて構いません。当然ですが、Nの数を増やせば増やすほど、計算時間が増えていきます。
# -*- coding: utf-8 -*-
import random
point = 0
N = 1000
for i in range(N):
x = random.random()
y = random.random()
if x*x+y*y < 1.0:
point += 1
# 円周率の近似解
pi = 4.0 * point / N
print(pi)
// 3.104自分の環境ではNを1000にした場合は、円周率の近似解は3.104と表示されました。
グラフに点を描写していく
今度はPythonのグラフ描写ライブラリであるmatplotlibを使って、上記にある画像みたいに点をプロットしていき、画像を出力させていきます。以下が実際のソースです。
# -*- coding: utf-8 -*-
import random
import matplotlib.pyplot as plt
point = 0
N = 1000
for i in range(N):
x = random.random()
y = random.random()
if x*x+y*y < 1.0:
point += 1
plt.plot(x, y,"ro")
else:
plt.plot(x, y,"bo")
# 円周率の近似解
pi = 4.0 * point / N
print(pi)
// 3.104
# 結果を表示
plt.gca().set_aspect('equal', adjustable='box')
plt.grid(True)
plt.xlabel('X')
plt.ylabel('Y')
plt.show()上記を実行すると、以下のような画像が画面上に出力されるはずです。

Nの回数を減らしたり増やしたりしてみる
点を打つ回数であるNを減らしたり、増やしたりしてみることで、徐々に円の形になっていく様子がわかっていきます。まずはNを100にしてみましょう。
# -*- coding: utf-8 -*-
import random
import matplotlib.pyplot as plt
point = 0
//ここを変える
N = 100
for i in range(N):
x = random.random()
y = random.random()
if x*x+y*y < 1.0:
point += 1
plt.plot(x, y,"ro")
else:
plt.plot(x, y,"bo")
# 円周率の近似解
pi = 4.0 * point / N
print(pi)
// 3.104
# 結果を表示
plt.gca().set_aspect('equal', adjustable='box')
plt.grid(True)
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
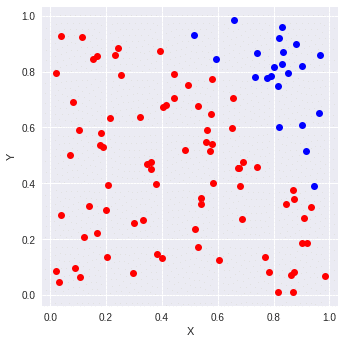
Nの回数が少ないため、これではまだ円だとはわかりづらいです。次にNを先程より100倍して10000にしてみましょう。少し時間がかかるはずです。
Nを10000にしてみると、以下の画像が生成されるはずです。綺麗に円だとわかります。
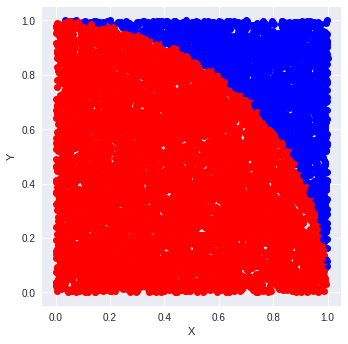
標準出力の結果も以下のようになり、円周率も先程より3.14に近づきました。
試行回数: 10000
円周率: 3.1592今回はPythonを用いて円周率の近似解を求めるサンプルを実装しました。主に言語やフレームワークなどのベンチマークテストなどの指標に使われたりすることもあるそうです。
自分もフレームワークのパフォーマンス比較などに使ったりしています。