自然言語処理の基礎であるTF-IDFの計算方法とPythonによる実装方法を解説
自然言語処理について基礎から勉強し直しており、今回はその勉強し直した内容のアウトプットも兼ねて基礎であるTF-IDFの数式からコードでの実装方法についても解説していきます。
データーである文字列を機械学習で扱える形式である数値に変換します。これらを主にベクトル化とも言いますが、様々な手法があります。
一番シンプルなものにはBowと呼ばれる手法があります。Bowについては以前こちらでも記事にしました。
TF-IDFとは
Bowの他にもう一つ上げられる手法として、TF-IDFというものがあります。こちらはTFとIDFを組み合わせたものであり、一言で言えば「文章中の単語の重要度を評価する」というものです。まずはTFとIDFについてそれぞれ説明します。
TF-IDFは以下のようにTFとIDFを掛け合わせたものです。
TF-IDF = TF x IDF
TF(Term Frequency)とは
TFはTerm Frequencyの略です。これは各文章内での単語の出現頻度を表しています。たくさん出現する単語ほど重要である事を意味しています。
数式としては以下になります。ある単語tがある文章d中に何回出現したかを表しています。
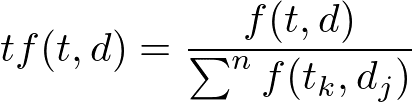
分子は「ある単語(t)の文章(d)内での出現回数(文章d内の指定単語tの出現回数)」を表しています。
分母は文章内の全単語の出現回数です。(数式的にはΣでそれぞれの単語の出現回数の和を表しています。)
TF値としては0 ~ 1の値を指します。
一つ簡単な例で実際に計算してみましょう。二つの簡単な文章AとBがあるとします。
文書Aを「リンゴとミカンとミカン」,もう一方の文書Bを[リンゴとバナナ]だとします。
文章A [リンゴ, ミカン, ミカン]
文章B [リンゴ, バナナ]
tf(リンゴ, 文章A) = 1/3 = 0.33
tf(ミカン, 文章A) = 2/3 = 0.66
tf(リンゴ, 文章B) = 1/2 = 0.5
tf(バナナ, 文章B) = 1/2 = 0.5
IDF(Inverse Document Frequency)とは
IDFはInverse Document Frequencyの略です。それぞれの単語がいくつの文書内で共通して使われているかを表します。「逆文書頻度」とも呼ばれており、単語がレアであるほど高い値を指し、「色々な文章によく出現する単語」なら低い値を指します。
数式としては以下になります。ある単語(t)がある全文書集合(D)中のどれだけ文書で出現したかの逆数になります。
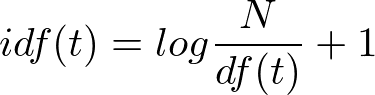
分子は全文書数を表しています。全ての文章の数です。
分子であるDFは「ある単語(t)が出現する文章の数」です。
こちらも一つ簡単な例で実際に計算してみましょう。二つの簡単な文章AとBがあるとします。
前回同様に文書Aを「リンゴとミカンとミカン」,もう一方の文書Bを[リンゴとバナナ]だとします。
文章A [リンゴ, ミカン, ミカン]
文章B [リンゴ, バナナ]
idf(リンゴ) = log(2/2) + 1 = 1
idf(ミカン) = log(2/1) + 1 = 1.3
idf(バナナ) = log(2/1) + 1 = 1.3
TF-IDFを掛け合わせる
上記で求めたTFとIDFの値を掛け合わせる事でTF-IDFを求めることができます。
tf_idf(リンゴ, 文章A) = tf(リンゴ, 文章A) * idf(リンゴ) = 0.33 * 1 = 0.33
tf_idf(ミカン, 文章A) = tf(ミカン, 文章A) * idf(ミカン) = 0.66 * 1.3 = 0.858
tf_idf(リンゴ, 文書B) = tf(リンゴ, 文章B) * idf(リンゴ) = 0.5 * 1 = 0.5
tf_idf(バナナ, 文章B) = tf(バナナ, 文章B) * idf(バナナ) = 0.5 * 1.3 = 0.65
Pythonでの実装
TF-IDFを求める関数はscikit-learnのsklearn.feature_extraction.textの中にあるTfidfVectorizerになりますが、ここでは実際に自分で実装してみましょう。
TF値を求めるソースは以下になります。文章となるdの部分には品詞ごとに区切ったリストを与えます。(今回の例では英単語を与えています)
def tf(t, d):
return d.count(t) / len(d)
tf = tf('word', ['word', 'test', 'hoge', 'sample'])IDFを求める計算式は以下になります。logはPythonの標準パッケージであるmathに組み込まれています。
コード上ではわかりやすくするためにも分母部分を指すDFを別関数で分けています。
idfの第二引数には全ての文章を与えます。今回はそれぞれの文章毎にリストに格納しています。
from math import log
def df(t, docs):
df = 0
for doc in docs:
df += 1 if t in doc else 0
return df
def idf(t, docs):
N = len(docs)
return log(N/df(t, docs)) + 1
# ベクトル化する文字列
text = [
'Apple computer of the apple mark',
'linux computer is unix like',
'windows computer'
]
idf_v = idf('computer', text)今回は下記にある3つの文章を使ってTF-IDF値を求めてみます。
Apple computer of the apple mark
linux computer is unix like
windows computer
コード全体は以下になります。vectorizer_transformというメソッドに文章のリストを与えることでTF-IDF値にベクトル化します。
# 単語を生成
words = []
for s in text:
words += s.split(' ')
words = list(set(words))
words.sort()上記の処理が途中挟みますが、やっている内容としてはユニークな単語のリストを生成しています。
from math import log
def tf(t, d):
return d.count(t) / len(d)
def df(t, docs):
df = 0
for doc in docs:
df += 1 if t in doc else 0
return df
def idf(t, docs):
N = len(docs)
return log(N/df(t, docs)) + 1
def vectorizer_transform(text):
# 単語を生成
words = []
for s in text:
words += s.split(' ')
words = list(set(words))
words.sort()
tf_idf = []
for txt in text:
line_tf_idf = []
for w in words:
# tfを計算
tf_v = tf(w, txt)
# idfを計算
idf_v = idf(w, text)
# tfとidfを乗算
line_tf_idf.append(tf_v * idf_v)
tf_idf.append(line_tf_idf)
return tf_idf
# ベクトル化する文字列
text = [
'Apple computer of the apple mark',
'linux computer is unix like',
'windows computer'
]
tf_idf = vectorizer_transform(text)
// print(tf_idf)
for line in tf_idf:
print(line)実行してみると以下が返ってきます。無事にTF-IDF値に計算できています。
[0.06558163402087844, 0.06558163402087844, 0.03125, 0.0, 0.0, 0.0, 0.06558163402087844, 0.06558163402087844, 0.06558163402087844, 0.0, 0.0]
[0.0, 0.0, 0.037037037037037035, 0.07772638106178185, 0.07772638106178185, 0.07772638106178185, 0.0, 0.0, 0.0, 0.07772638106178185, 0.0]
[0.0, 0.0, 0.0625, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.13116326804175688]ソースコードは以下に載せてあります。