AlphaZeroの解説
囲碁、将棋、チェスといったボードゲームで、人間を超える強さを持つAIが存在することが知られています。これらのAIは、自ら対局を重ねることで学習データを生成し、それに基づいて学習を行います。外部のデータは必要としません。
私が自らAlphaZeroのアルゴリズムを用いてオセロを学習させた際、AIがボードの角を制する戦略が有利であることを学んだようで、角を積極的に取る行動を見せました。この振る舞いには、ほのかな感動を覚えました。
2017年に、DeepMindは囲碁専用AI "AlphaGo Zero" に関する論文1『Mastering the game of Go without human knowledge』を発表しました。チェスや将棋など様々なボートゲームに適応可能なAI "AlphaZero" を開発し、その成果を論文2『Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm』で公表しました。AlphaZeroの名称に含まれる "Zero" は、初期知識なしで自己学習によって高度なスキルを身につけることができる、という意味が込められていると思います。
AIモデルが自ずと強くなるためにはどのような学習プロセスを踏んでいるのでしょうか。
学習サイクル

【モデルの初期化】
最初に、未学習の状態のモデルを準備します。学習されていない状態なので、とてつもなく弱い状態です。
【セルフプレイ】
一つのモデルを用いて、ゲームを自動で複数回対戦させ、その過程で学習データを生成します。AlphaZeroの論文では明示的に回数は示されておりませんが、AlphaGo Zeroの場合の対戦数は25000回とされています。適度な数値はモデルの規模やゲームの複雑度にも依存するはずです。小さすぎるとモデルが学習時に強くならない、大きすぎても学習に時間がかかりすぎるため、適度な値を見つける必要がありそうです。
【学習】
セルフプレイで生成されたデータを用いてモデルを更新します。データをバッチに分けて、各バッチに対してモデルのパラメータを更新します。
モデルの初期化の後、セルフプレイと学習を繰り返し行い、モデルを徐々に強化していきます。具体的には、「モデルの初期化 → セルフプレイ → 学習 → セルフプレイ → 学習 → セルフプレイ → … → 学習」を繰り返し行い、性能を向上させます。

次に、AlphaZeroのモデルの詳細をみていきます。
AlphaZeroに使われるニューラルネット
インプットデータ
グリッド上で行われるボードゲームは、ニューラルネットの畳み込み層と親和性が高く、ボードゲームの状態を空間的なパターンとして認識し、局面の特徴を抽出するために使用されます。よって、入力データの構造は単純化せずに、ボードの形式を維持した状態でモデルに入力することができます。
論文を基に将棋の例を考えます。
どの駒がどの位置にあるのかを表現するために、以下のように駒があるセルには「1」、駒がないセルには「0」を入れます。各駒の種類で分けてボードを用意します。

上では、「歩」「王」「と」の例ですが、将棋の駒の種類には以下の計14種類があります。
「歩」、「香車」、「桂馬」、「銀」、「金」、「飛車」、「角」、「王」
「と」、「成香」、「成桂」、「成銀」、「竜王」、「竜馬」
計14のボードで駒の位置情報を保持します。
また、将棋では相手の駒を取って使用することができるため、どの駒をいくつ持っているかの情報も表現する必要があります。
「歩」、「香車」、「桂馬」、「銀」、「金」、「飛車」、「角」
計7のボードで持ち駒の情報を保持します(※)。
全てのボードを重ねると以下の三次元データになります。

論文では、過去の8局面まで含め、その他情報も含めることにより、トータル362枚の画像をインプットデータにしています。
画像の数は論文1のTable S1からみられます。

※ Prisoner countは持ち駒のカウントであるが、具体的にどのように数値が入っているのか論文では詳しい情報が書かれていないようです。(多分すべてのセルに同じカウント数が入ると思います。)
モデルの構造
畳み込み層で特徴を抽出と処理を行い、所々でデータの正規化またReLU層で不要な情報を除く処理を行っています。また、スキップ接続により大きい規模のモデルでも学習の重みパラメータ調整時に勾配が消失しない構造になっています。
入力は三次元に用意されたボード状態の情報、そして出力は次の手の確率と現局面の価値の二つになります。
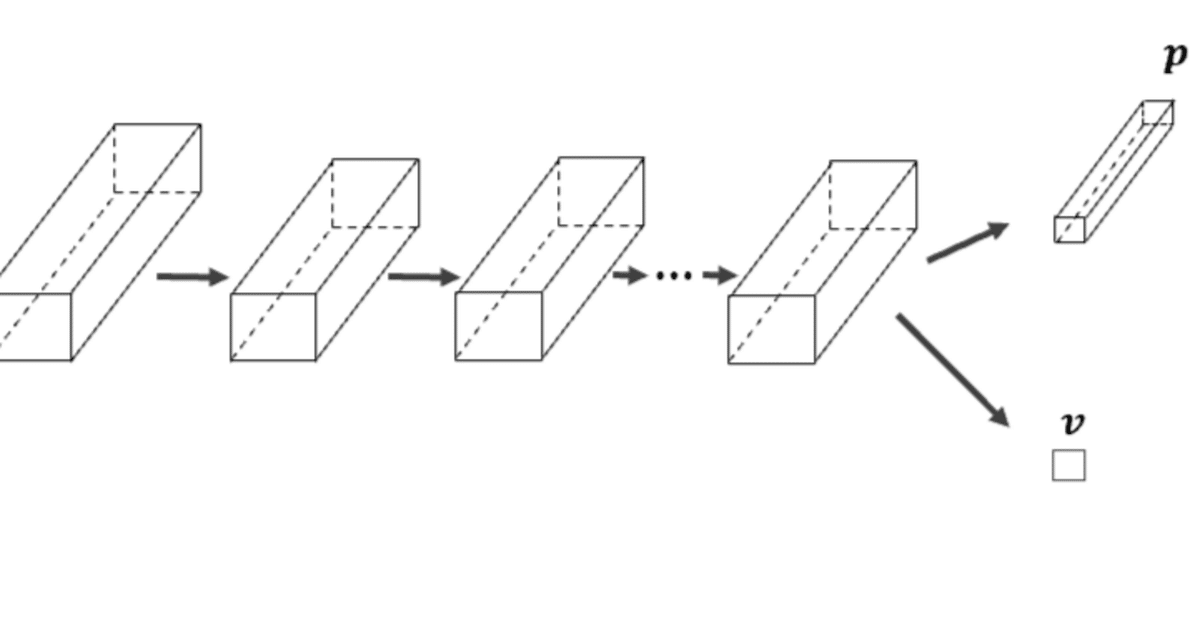
以下の図はデータの流れを入力から出力まで図にしたものです。出力の$${p}$$は「次の手の確率」、$${v}$$は「現局面の価値」として使用されます。

①~④の処理プロセスは以下の構造を示しています。

畳み込み層、正規化、ReLU活性化を含むブロックを繰り返し適用することで、データからより抽象的で有用な特徴を段階的に抽出する構造になっています。
②のブロックはスキップ接続を含み、複数同じブロックが連結しています。
④から出力される結果は「現局面の価値」となります。Tanh層を通すため、出力は-1から+1の間を取ります。
③から出力される結果は「次の手の確率」になります。(※)
※推論時には、後続処理が必要になります。ルール上で次の手が打てないセルは0にマスキングを行い、すべての数値を合計で割ることにより確率分布を計算します。
次の手の確率
pがどのような情報を保持しているのでしょうか。

出力の形式は工夫次第でありますが、論文の内容を基に将棋の場合をみてみましょう。
どの位置にどのアクションで動かすかの情報が$${p}$$に含まれます。

以下でアクション数をカウントすると、
各方向(上、下、右、左、右上、右下、左上、左下)には、最大8マス動かすことができるため、最大で8x8=64通り
駒を動かした後に成る場合もあるので、加えて同じく64通り
桂馬には2通り
桂馬を動かした後に成る場合もあるので、加えて同じく2通り
どの持ち駒(歩、香車、桂馬、銀、金、飛車、角)を使うかで7通り
合計が139通りになります。
そして、どの位置にどのアクションで動かすか考慮すると、$${9\times 9 \times 139=11259}$$通りになります。
駒の情報は出力自体には含まれなくても、位置とアクションがわかれば駒を特定することができます。

学習データ
機械自身で対戦したデータが学習データに使用されます。
ゲームの勝敗が現局面の価値の正解データとして使われます。
ゲームで勝った場合は「+1」、負けた場合は「-1」、引き分けの場合は「0」が使われます。
1ゲーム内の勝者のすべての局面の価値は「+1」、敗者のすべての局面の価値は「‐1」、引き分けの場合は両者のすべての局面の価値は「0」となります。
ゲームを通して、敗者のすべての局面が悪い場合がないかもしれないため、「-1」とラベル化されるのが気になるところです。しかし、そもそもの局面の状態の良し悪しを判断するのは困難なタスクだと思われるので、勝敗ベースにラベル化するのは納得です。
ニューラルネットだけでは、「次の手の確率」が最善の手かわかりません。「現局面の価値」をうまく活用する必要があります。先読みを行い、後に続く局面の価値をうまく使うことにでより最善の手を見つけることができます。よって、AlphaZeroでは探索ツリーとニューラルネットを組み合わせて推論をおこないます。
AlphaZeroモデル(推論時)
どの次の手を打つか決めるために、探索ツリー(モンテカルロ木探索)とニューラルネットを使用します。すべての通りを先読みせずに、自分と相手にとって有利な手を探索する仕組みになっています。
毎回のターンで、探索ツリーを作成してその木を基に次の手を決めます。ニューラルネットは木の作成プロセスで使用されます。
木の作成プロセス
木の作成プロセスでは「選択」「展開」「評価」「更新」を繰り返し行います。
以下のプロセスをN(=試行回数)回繰り返します。
【選択】
1番評価の高い(展開済みの)局面を選択
【展開】
次の局面を展開(※)
【評価】
選択した局面をニューラルネットに入力して、「次の手の確率分布」と「現局面の価値」を取得(※)
【更新】
試行回数と局面の価値を全ての親ノードに更新する
※最終手の場合は、展開は行わず、現局面の価値は+1, 0, -1のいずれかをとります。


相手のターンで評価された「局面の価値」は、自分にとっては逆の意味を持ちます。よって、更新を行う場合、マイナスの値を付けて数値を足し合わせます。


上の例を使い、次の手を決定するロジックにはいります。ルートノードの直下の子ノードの試行回数は78回と22回となっているため、それぞれ選択する確率を以下で表現すると
$${p_1 = \frac{78^{1/\tau}}{78^{1/\tau}+22^{1/\tau}}, \quad p_2 = \frac{22^{1/\tau}}{78^{1/\tau}+22^{1/\tau}}}$$
$${\tau}$$は温度パラメータで、0に近い値に設定されると、最も試行回数が多い手が選ばれる確率が高くなります。$${\tau}$$が1の場合は試行回数に比例した確率で手が選ばれ、より大きくなるほど選択がランダムに近づくことになります。$${\tau}$$を調節をすることによりランダム性を設定することができます。
選択のロジック
自分のターンの際は自分にとって良い次の手を選択します。一方で、相手のターンの際は相手にとって良い次の手を選択するべきです。
次の手を選択するために「探索」と「活用」のバランス
ある局面$${s_t}$$で最適な次の手$${a_t}$$を選択するために、以下の式を使います。
$${a_t = \argmax_{a} (Q(s_t, a) + U(s_t, a))}$$
$${Q}$$は「知識の活用」、$${U}$$は「探索」の意味合いを持ちます。
$${U}$$は「探索」の意味合いを持ち、ニューラルネットによる次の手の確率が影響を持ちますが、試行回数が多くなるにつれ影響が小さくなります
$${Q}$$は「知識の活用」の意味合いを持ち、ニューラルネットから出力される局面の価値の平均値をとります
ここまで読んでいただき誠にありがとうございました。
この記事が少しでもお力になれるとうれしいです。
参考資料
(論文1) Mastering the game of Go without human knowledge
(論文2) Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm
