
1. AIでよく使われる数学:記法を克服版(都度更新)
機械学習の分野でよく使われる数学は微分、積分、線形代数であり、大学1,2年で学ぶ内容のため、数学のハードルは比較的低いと感じる数理系の方もいらっしゃるでしょう。
とはいえ、中学高校数学がままならない場合は少しハードルが高く数学で挫折をしてしまうかもしれません。
機械学習の分野では機械が学習をする仕組みを考えるため、人間の学習する過程にたくさんのヒントがあるはずで、経験や常識を上手く適用できる非常に興味深い分野だと感じています。そして誰もが様々な形で貢献できる分野だと信じています。そのため数学が個々のポテンシャルを妨げるのはもったいないと感じている次第です。
私はもとから数学が得意だったわけでなく、周りよりも学ぶスピードが遅かったと思います。しかし、勉強を持続することにより次第に慣れてきました。
当時、留学をしていたので、話せなかった英語が次第に話せるようになったかのように、使っていれば体が慣れてくる感覚と似ていました。数学は論理的で数式の操作をイメージするかと思いますが、直観的理解も重要であり概念を可視的、比喩的、感覚的に理解を深めることができます。
記憶が苦手な私は、用語などは忘れるがちですが、感覚は記憶に残りやすいため具体的な定義などを思い出す手助けになります。
良く出てくる数学の記法や超基礎概念について、一旦まとめようと思います。
基礎的な概念に触れつつ記法に着目します。記法に慣れることは大きな一歩です。
🌸変数
任意の数値を表す記号。
数学ではさまざまな数を取り扱うため、これらを一般的に表現するために変数を使用します。
変数は変わり得る値を表し、通常はアルファベットで表記されます。これに数値を代入することで、さまざまな計算を表現できます。
以下の表現を考えてみます。以下では$${x}$$を変数としています。
$$
\large 2 x + 1
$$
上では$${x}$$に自由に数値を代入してよいですよ、といった表現になっています。とりあえずいろいろな数値を代入して、テーブルにまとめてみると
$$
\begin{array}{|c|c|r|} \hline
x & 2x+1 \\ \hline
0 & 1 \\ \hline
1 & 3 \\ \hline
2 & 5 \\ \hline
3 & 7 \\ \hline
4 & 9 \\ \hline
5 & 11 \\ \hline
\end{array}
$$
「2を掛けて1を足す操作」を$${2x+1}$$が行っているのが分かります。変数を使って表現すると、数値に対してどのような操作を行うのかを定義していることになります。
🌻ポイント🌻
$${x}$$に限らず、変数を記述するためにさまざまなアルファベットやギリシャ文字がよく使用されます。数値を代入可能であることを示すためのもので、基本的には何でも良いのです。
🌸関数
入力と出力の対応関係。
$${2x+1}$$に変数の値を決めると、2を掛けて1を足し合わせた値が返ってくることがわかりました。ここでの関数は、$${x}$$の値とそれに対応する1つの値の関係を意味します。
以下の式では、$${f(x)}$$は$${2x+1}$$と定義されており、$${x}$$の任意の値に対して計算される出力を$${f(x)}$$として表します。
$$
{f(x) = 2x + 1}
$$
コンパクトな表現で便利になっており、変数$${x}$$に$${1}$$を代入すると$${f(1)}$$と書くことができます。
$${f(x)=2x+1}$$の場合、$${x}$$の具体的な数値と$${f(x)}$$との関係をまとめると
$$
\begin{array}{|c|c|r|} \hline
x & f(x) \\ \hline
0 & 1 \\ \hline
1 & 3 \\ \hline
2 & 5 \\ \hline
3 & 7 \\ \hline
4 & 9 \\ \hline
5 & 11 \\ \hline
\end{array}
$$
🌻ポイント🌻
✾$${f(x)}$$に限らず、関数を記述するためにさまざまなアルファベットやギリシャ文字がよく使用されます。(例えば、$${g(x)}$$や$${y(x)}$$など)
✾関数$${f}$$は、そのルール自体を指し、$${f(x)}$$は$${x}$$を具体的な入力として$${f}$$を適用した場合の出力を表します。時には、入力が自明の場合や特定の議論の文脈で、$${f}$$のみで関数を指すことがあります。
🌸関数の可視化
変数$${x}$$の値に対してある値$${f(x)}$$が決まるため、ペアで考えてみましょう。
$$
\large (x, f(x))
$$
上の表現は点の位置として捉えます。
二つの垂直に交差する軸、すなわちx軸とy軸を持つ座標平面上に、点の位置をプロットすることができます。変数$${x}$$の値は$${x}$$軸上と一致、$${f(x)}$$の値は$${y}$$軸上と一致させます。
例えば、$${f(x)=2x+1}$$の場合、これまでの例を使うと$${(0, 1), (1, 3), (2, 5), (3, 7), (4, 9), (5, 11)}$$の6つの点が$${x-y}$$座標で描くことができます。

上記は六つの点のみ描きましたが、変数$${x}$$は他にも$${0.1}$$や$${0.3}$$、なんなら$${0.000003}$$などの値を取ることができ、無限個の数が存在します。無数の点を座標上にプロットすると、それらの点は連続した直線を形成します。

🌸極限
限りなく近づけること。
極限は、ある量が特定の値にどのように近づくか、または無限に大きくなるかを数学的に表現するのに用いられます。
例えば、$${f(x)=2x +1}$$によって描かれた直線を辿って点$${(1, 3)}$$に向かっている様子を表すと考えると、$${x}$$が$${1}$$に近づくにつれて、$${f(x)}$$が$${3}$$にどのように近づくかを表すことができます。

これを英語のlimitを記法に使い、以下の形で表現されます。
$$
\lim_{x \rightarrow 1}(2x + 1) = 3
$$
この記法は初見では複雑に感じるかもしれませんが、
変数$${x}$$の値を$${1}$$に限りなく近づけた結果、$${f(x)=2x+1}$$は$${3}$$となる、と解釈されます。
記法から確かにそんな感じに読み取れるな、と認識できていれば十分です。
次に、$${x}$$を限りなく大きくしてみます。$${100, 1000, 10000, 1000000}$$といったように、値が大きくなると桁の数も増えていき、永遠に桁が続いて終わりのないように感じます。
100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000………………..0
限りなく大きなものを$${\infin}$$(無限)と表記されます。
無限大$${\infin}$$とは、いかなる有限値よりも大きな概念です。どんなに大きな数値を想定しても、無限大はそれを超えると理解されています。
「$${2x+1}$$の$${x}$$を限りなく大きくすると、$${2x+1}$$も限りなく大きくなる」を以下のように表現します。
$$
\lim_{x \rightarrow \infin}(2x + 1) = \infin
$$
一方、分数$${\frac{1}{x}}$$の表現はどうなるでしょうか。ここでは限りなく大きい値で割ることになるので、0になります。
「$${\frac{1}{x}}$$の$${x}$$を限りなく大きくすると、$${\frac{1}{x}}$$は限りなく$${0}$$に近づく」を以下で表現します。
$$
\lim_{x \rightarrow \infin}\frac{1}{x} = 0
$$
🌸定数
特定の値が入る記号。
定数は、特定の固定値を示すために使用されます。これにより、数式や計算の中で一貫性を保つことができ、変数とは異なり、その値は変わりません。
特定の値が入るのであれば記号を使う必要がないようにみえますが、変数とどう違うのでしょうか。
関数$${f(x)=2x+1}$$は直線の形をとりますが、別の関数$${f(x)=x + 5}$$ も同じく直線の形をとります。
$${x}$$の前に掛けられている数値が増加のスピード、そして足し合わせている数値は上下の平行移動の役割をそれぞれが持ちます。この二つがどのような数値をとろうが直線の形をとります。
そして、汎用的に直線の公式を表現するため、文字で表現してみます。
$$
f(x) = a x + b
$$
全てアルファベットで表現されるがそれぞれが異なる意味合いを持ちます。
$${a}$$と$${b}$$は固定された値(定数)、
$${x}$$は変わりうる値(変数)。
二次関数も以下のように書けます。
$$
f(x) = ax^2 +bx + c
$$
使う際、定数には具体的な数値が与えられる、一方で変数は変わりうる値となります。
変数と定数を使うと、無数の表現を一つにまとめて形が見えやすくなっています。
🌸ギリシャ文字
変数もしくは定数。
急に見慣れないギリシャ文字に出会うことがあります。$${\alpha}$$(アルファ)、$${\beta}$$(ベータ)、$${\gamma}$$(ガンマ)など、ギリシャ文字が数学で使われることが良くあります。
ギリシャ文字を使って、直線の公式を書き直してみます。
$$
f(\xi) = \alpha \xi + \beta
$$
$${\alpha, \beta}$$は定数、$${\xi}$$は変数とします。
前の表現$${f(x)=ax+b}$$と比べると、ただ見栄えが変わっただけです。
ギリシャ文字を使用することによる数学的な意義は特にありませんが、伝統的に特定の概念を示すために用いられます。
例えば、$${\theta}$$は角度、$${\omega}$$は角速度、$${\sigma}$$は統計学だと標準偏差、などで使われたりします。
メリーゴーランドの馬の回転する速度は、中心からの馬の距離(半径)と角速度を掛けて計算できます。回転する速度の公式が以下のかたちで書かれます。
$$
v = r\omega
$$
$${r}$$が半径、$${\omega}$$が角速度であり、なんらかの数値がはいります。ここでのギリシャ文字$${\omega}$$が使われていることにより、角速度を意味しているのかな、と一目で認識することができます。なので、理解のし易さに役に立っています。
🌸微分
傾きのこと。
直線をグラフにしてみましょう。

下の4つの関数をグラフ化したものになります。
$$
\begin{matrix}
f(x) = 2 x + 1\\
\\
f(x) = x + 1\\
\\
f(x) = 1 \\
\\
f(x) = -x + 1
\end{matrix}
$$
直線の公式($${f(x) = ax + b}$$)において、定数 $${a}$$ は直線の傾きを表します。直線が $${x}$$ 軸に対してどれだけ傾いているかを数値で表します
$${a}$$ の値が正の場合、傾きは右肩上がりで、直線は左下から右上に向かって上昇します。一方、$${a}$$ の値が負の場合、傾きは右肩下がりで、直線は左上から右下に向かって下降します。
直線上に二つ点をとり、そして傾きは以下のやりかたで計算を行うことができます。

例えば、$${f(x) = 2 x + 1}$$の場合だと、
$$
\text{傾き} = \frac{f(4) - f(2)}{4 - 2} = \frac{9 - 5}{4 - 2} = 2
$$
$${x}$$が1増加したら、$${f(x)}$$は2増加しますよ、ということになります。
傾きが$${2}$$と求まりました。直線上どの2点をとり計算しても、同じく$${2}$$が求まります。
直線のため、傾きが一定のためです。
では曲線の場合はどうでしょう。以下の曲線は$${f(x) = x^2}$$をグラフにしました。

任意の2点のペアを取ると、以下のように直線の傾きは変わります。

やはり2点の取り方で直線の傾きが変わってしまいます…
つぎに、この2点が一致するまで近づけてみます。
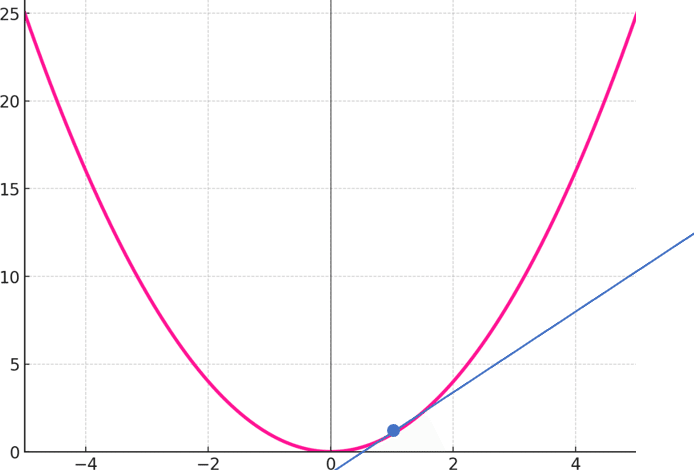
そうすると、一点で曲線に接する直線が描かれます。
微分は接点を通る直線の傾きをみつけることができます。
また、微分は曲線のある点における瞬間的な変化率を表し、その点における接線の傾きを計算するために用いられます。
以下に微分の定義を書き下しますが、極限の記法が出てきます。これは二点の幅を限りなく小さくする意味をもっていて、二点の幅を$${h}$$で表現しています。
$$
\large f'(x) = \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}
$$
記法となる$${f'(x)}$$は、関数$${f(x)}$$の任意の点$${x}$$における接線の傾きを示しています。導関数と呼ばれています。
以下の記法も$${f'(x)}$$と同じ意味で良く使われます。
$$
\large \frac{df}{dx}(x)
$$
🌸総和
総和$${\sum}$$は足し算をコンパクトに表現する便利な記法です。
例えば、$${1}$$から$${100}$$までの整数の足し算を書き下すと
$$
\large 1 + 2 + 3 + 4 + 5 + \cdots + 100
$$
となり全ての数値を書くのは大変です。「$${\cdots}$$」で省略せずに書くために、総和を使うとコンパクトに書けます。
ここで、$${j}$$は1から100までの整数を順に取るインデックスです。
$$
\large \sum_{j=1}^{100}j = 1 + 2 + 3 + \cdots + 100
$$
$${\sum}$$の下側にある$${j=1}$$は始まりのインデックス、また上側にある$${j=100}$$は終わりのインデックスを意味します。$${j}$$は変数として扱われ、$${1}$$から$${100}$$まで入力されたものが足し合されます。
データの分析では総和をよく目にします。
$$
\begin{array}{|c|c|r|} \hline
a & b \\ \hline
4 & 1 \\ \hline
2 & 3 \\ \hline
4 & 5 \\ \hline
3 & 4 \\ \hline
4 & 3 \\ \hline
5 & 3 \\ \hline
\end{array}
$$
上のテーブルには$${a}$$と$${b}$$のカラムがあり、それぞれの値を記号で表してみます。
$${a_1=4, a_2=2, \cdots, a_6=5}$$
様々な統計量をコンパクトに表現できます。
例えば、
平均値を計算するには、$${a}$$の値の総和を要素数で割ります。
$$
\frac{1}{6}\sum_{j=1}^6a_j=3.666\ldots
$$
また機械学習でよくでてくる平均二乗誤差では、$${a-b}$$の二乗値の総和を要素数で割ります。
$$
\frac{1}{6}\sum_{j=1}^6(a_j-b_j)^2 = 14.83\ldots
$$
🌷補足🌷
総乗と呼ばれるのは、$${\prod}$$の記法が使われ、掛け算をコンパクトに表現します。例えば、複数の確率の積を計算する際などに用いられます。
🌸積分
積分は、関数の下に描かれる図形の面積や立体の体積を計算する手法です。

複雑な曲線の下の領域を評価する際に、四角形を多数並べて近似します。
四角形の面積(高さ×幅)を計算すると

この四角形を並べると

これらの四角形の幅を徐々に小さくし、数を増やすことで、曲線下の面積の近似が改善されます。

四角形の数を限りなく増やした場合、面積を正確に表現することができます。
$${x=a}$$から$${x=b}$$までの区間を、$${n}$$個の四角形に分け、$${k}$$番目の四角形の高さと幅をいかのように表現できます。

この四角形を無数に並べたものを以下で表現します。

上の表現では少し複雑にみえるため、簡単に表現したのが
$$
\int_a^bf(x)dx
$$
として書かれます。$${x=a}$$から$${x=b}$$まで関数$${f(x)}$$の下の面積を求めることを意味します。
🌷補足🌷
変数の数が増えると、積分が行われる空間の次元も増加し、その結果、積分によって求められる領域の体積(ボリューム)が計算されます。
🌸行列
行列は、数値や変数を行と列で並べた形で表現される数学的な構造です。
例えば
$$
\begin{pmatrix}
3 & 2 \\
1 & -1\\
5 & 0
\end{pmatrix}
$$
行と列のサイズを示すために、$${n \times m}$$行列として書かれます。ここでの$n$は行の数、$${m}$$は列の数を示します。なので上記の行列は$${3\times 2}$$行列の形をとっています。
行列の表記に関しては、カッコの使用(丸括弧()や角括弧[])どちらも使われますが、意味は同じです。
行列をアルファベットで表現する場合、一般的には大文字で太文字が使われます。
例えば、
$$
\textbf{A} =
\begin{pmatrix}
3 & 2 \\
1 & -1\\
5 & 0
\end{pmatrix}
$$
そうすると、見てすぐに行列だと認識することができます。
また、行列の要素の値を示すために
$$
a_{ij}
$$
とよく書かれたりますが、$${i}$$行$${j}$$列の要素を意味しています。例えば、行列 $${\textbf{A}}$$ の場合、$${a_{22}}$$ は第2行第2列の要素を意味し、ここでは -1 です。
次に、列ベクトルと呼ばれるものがありますが、$${n\times 1}$$行列を示しており、1列しかない行列の意味をします。
$$
\textbf{a} =
\begin{pmatrix}
3 \\
1 \\
5
\end{pmatrix}
$$
一方で、行ベクトルと呼ばれるものもあります。これは$${1\times m}$$行列を示しており、行が1行しかない行列の意味をします。
$$
\textbf{b} =
\begin{pmatrix}
3 & 2
\end{pmatrix}
$$
上記でわかるように、ベクトルの表記は小文字で太字がよく使われます。もしくは$${\vec{a}}$$といった表記も使われたりします。
🌸行列の和と積
行列は長く複雑な式や表現をコンパクトに書けるためとても便利な役割を担っています。
行列の和と積の性質に慣れると行列を便利に扱えます。
まず、行列の和はシンプルに要素毎に和をとります。
$$
\begin{pmatrix}
3 & 2 \\
1 & -1\\
5 & 0
\end{pmatrix}
+
\begin{pmatrix}
-1 & 0\\
3 & 4 \\
-2 & 1
\end{pmatrix}
=
\begin{pmatrix}
2 & 2\\
4 & 3\\
3 & 1
\end{pmatrix}
$$
要素毎に和を取るため、行列のサイズは同じである必要があります。
次に、行列の積を取る場合、
すこーしややこしいですが、慣れが必要であることと、この構造が後にとても便利になります。
以下のように二つの行列を並べて書くと積を意味します。
$$
\begin{pmatrix}
2 & 1\\
-1 & 0
\end{pmatrix}
\begin{pmatrix}
3 & 1\\
2 & -1
\end{pmatrix}
$$
積の取り方は以下の流れになります。(私は腕を横から縦に時計回りに振るイメージで最初は覚えました。。)




上記の計算から積が求まりました。
$$
\begin{pmatrix}
2 & 1\\
-1 & 0
\end{pmatrix}
\begin{pmatrix}
3 & 1\\
2 & -1
\end{pmatrix}
=
\begin{pmatrix}
8 & 1\\
-3 & -1 \times 1 + 0 \times (-1)
\end{pmatrix}
$$
🌻ポイント🌻
積を取るには、左行列の列の数と右行列の行の数が一致する必要があります。
🌸連立方程式の行列表現
複数の方程式が組み合わさったものを連立方程式と呼びます。
機械学習においても、さまざまな場面で連立方程式が利用されます。
$$
\large
\begin{matrix}
3 x + 2y = 1 \\
x - y = -1
\end{matrix}
$$
行列を使い、同じ表現をすることができます。
$$
\large
\begin{pmatrix}
3 & 2 \\
1 & - 1
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=
\begin{pmatrix}
1 \\
-1
\end{pmatrix}
$$
ベクトルと行列を用いた表記でコンパクトに書くことができます。
$$
\textbf{A}\textbf{x}=\textbf{b}
$$
連立方程式をより一般的に表記してみましょう。
$$
\large
\begin{matrix}
a_{11}x_1 + a_{12}x_2 +a_{13}x_3 + \cdots + a_{1m}x_{m} = b_1 \\
a_{21}x_1 + a_{22}x_2 +a_{23}x_3 + \cdots + a_{2m}x_{m} = b_2 \\
\vdots\\
a_{n1}x_1 + a_{n2}x_2 +a_{n3}x_3 + \cdots + a_{nm}x_{m} = b_n \\
\end{matrix}
$$
行列で表現すると
$$
\large
\begin{pmatrix}
a_{11} & a_{12} & a_{13} & \cdots & a_{1m} \\
a_{21} & a_{22} & a_{23} & \cdots & a_{2m} \\
\vdots & \vdots &\vdots & \ddots &\vdots\\
a_{n1} & a_{n2} & a_{n3} & \cdots &a_{nm}\\
\end{pmatrix}
\begin{pmatrix}
x_1\\
x_2\\
\vdots\\
x_m
\end{pmatrix}
=
\begin{pmatrix}
b_1\\
b_2\\
\vdots\\
b_n
\end{pmatrix}
$$
そしてこれもコンパクトに
$$
\textbf{A}\textbf{x}=\textbf{b}
$$
と表現できます!
一旦、ここまでです。読んでいただきありがとうございました。何かの役に立てばうれしいです。お気軽にお問い合わせいただければと思います。
私は大学院で数学の研究を始めて、博士号取得後にポスドク、最終的に企業に移り機械学習関連の業務に関わってきました。現在は個人で講師や分析支援などをしていますが、特に教育分野に非常に興味を持っており、誰もが活躍できる場を作りたいと考え、新しい事業の立ち上げを目指しています。仲間も探しています!
