
t=2^xでtが2つの整数解ならなぜ2^xのxも2つの整数解と言えるの?「逆関数と座標を使って理解する二次方程式の解」
数学の世界では、方程式を解くことは日常茶飯事ですが、時にはその解の背後にある理由を深く理解することが重要です。今回は、
t = 2^xをxについての多次元方程式で代入すれば、tについての二次方程式となるような場合、 t についての二次方程式が異なる2つの正の実数解を持つ場合、t=2^xで代入した右辺の2^xのxの解 も異なる2つの正の実数解を持つ理由について考えてみましょう。
通常 t で置き換えると、t についての二次方程式に変換されます。そして、この二次方程式が異なる2つの正の実数解を持つ場合、直感的には元の t=ax^2 の x も異なる2つの正の実数解を持つのだと。その理由?t=ax^2だからだと暗記的に考えがちです。しかし、なぜそうなるのでしょうか?
この疑問を解決する鍵は、逆関数と座標の考え方にあります。
なぜ逆関数?
関数は点の集合で、ある点は関数のグラフの中の1つの点だとします。逆関数は、元の関数とy=xに対して対称なので、元の関数の中のある1点とy=xに対称な点が、逆関数の中の任意の1点となります。
例えば、t=2^xで、例えば多次元方程式(最大次数の項は2^xの整数倍)で、2^x=tとおいて、tについての二次方程式にし、tが異なる2つの正の解を持つとき、t軸上でtについての二次方程式=0の2つの実数解は、
t軸と2点で交わり、その2点は(α、0)、(β,0)であらわされ、αとβはどちらも正の数です。ここまではtが2つの整数解を持つ場合の解とt軸のアバウトな位置関係です。(正の整数解についての条件についての説明は省略しています)
tが2つの正の実数解なので、t=2^xであらわされる場合、指数x≧0となるので、右辺>0となるという理論でも解決できますが、今回は逆関数を使い、tについてのf(t)=0のときの正の2つの解の逆座標2点が、t=2^xの逆関数上の任意の2点なら、tが(α、0)(β,0)なら、逆座標は(0、α)(0、β)でどちらのα、βも正の整数だから、t=2^xでtが正数ならxも整数になるという別解的な考えです。
右辺の2^xをtについての二次方程式に代入(戻す)をするとき、そのxも異なる2つの正の実数解であると考えるためには、tについての二次方程式f(t)という放物線のf(t)=0としたときのtの解、それは座標軸であらわすとtを代入したとき、yの値が0となる座標なのでそれはt軸と放物線の交点(α、0)、(β,0)です。
このとき、y=xについて対称な点が(0,α)、(0,β)となります。
つまりf(t)とy=xについて対称なグラフがt=2^xの逆関数で、その逆関数とy軸との交点(逆関数上の任意の1点とも考えられる)(0,α)(0、β)は(α、0)(β、0)が正の整数解なら、(0,α)(0,β)も整数解だよねとなります。
回転行列でもイメージできる逆関数
ちなみに逆関数の考え方について、あるグラフの逆関数はy=xに対して対称なので、それは、もとのグラフを時計まわりに45度回転移動させた場合、逆関数のグラフと重なります。もしくは、逆関数のグラフを45度反時計まわりに回転させれば、もとのグラフと重なります。回転させなければ、もとのグラフと逆関数は、y=xに対して対称なグラフとなっています。
イメージとしては、元のグラフと逆関数は動かさず固定し、xy軸だけを反時計まわりに45度回転させるとx軸とt=xのグラフが重なります。
この状態で、元の関数のグラフ上にあるすべての点を、x軸に対して対称移動させたときの点が点Bとなっているイメージです(グラフ回転→回転後のx軸に対称な2点)。
座標軸回転による点の移動は回転行列で逆座標を求めることもできました。
t=2^xの逆関数の求め方
ここではt=2^xを代入したtについての二次方程式はおいておき、t=2^xについてのみの話です。t=2^xの逆関数は、まずxとyを入れ替えて、それからyについて解きます。
t=2^xは縦軸がt、横軸がxです。

ここで、xとtを入れ替えます。すると
x=2^t になります。

このままでは、x軸が主軸の縦軸、t軸が横軸になってしまうので、
もとの状態であるt軸が主軸である縦軸、x軸を横軸に戻すために、tについて解くと、
t=log2(x)
でこれがt=2^xの逆関数となります。

元の関数のyとxを入れ替えて、「x=~」の形にしてしまうのと、そこからさらにyについて解いた後のグラフは同じ軌道ですが、もとのグラフでは従属変数であるyが左辺、独立変数が右辺なので、入れ替えると従属変数がxになってしまいます。これだと右辺の独立変数yによって、xの値が決まることになってしまうので本末転倒となるので、左辺にyを持ってくるために、xとyを入れ替えた関数をyについて解いているんだなと思いました。
ここで、
t=2^xの指数関数では、指数がx、底が2、tが真数です。
t=log2(x)の左辺tは指数、2は底、xは真数です。
真数というのは、たとえば、16=4^2のとき、16のことです。底は4のことで、指数が2のことです。指数関数では、真数(従属変数y)=底^指数(独立変数x)の形で表すんですね。
一方、対数関数は、指数(従属変数y)=log(底)(真数:独立変数x)になります。y=2^xという指数関数について、
指数xについて解くと、
x=log2(y)
これは、指数xを指数関数で表した場合と対数関数で表した場合になるので、同じグラフとなるんだなの発見。
このとき、元の関数y=2^xの逆関数を求めてみると、まずxとyを入れ替えますると、x=2^yとなります。

このとき、グラフの位置関係としては、2つのグラフはy=xに対して対称なので、逆関数と元の関数の位置関係と同じです。
逆関数ではy=xに対称であるほか、f(x)の逆関数がg(x)のとき、
f(g(x)) = x および g(f(x)) = x が成り立ちます。
上記のグラフで指数関数である元の関数
y=2^x
=f(x)
とその逆関数のうち、
指数関数で表されている
x=2^y(対数関数ならy=log2(x))
=g(x)について、
f(g(x))=2^(2^y)=(2^2)^y=4^y
g(f(x))=2^(2^x)=(2^2)^x=4^x
で、
f(g(x)) = x および g(f(x)) = xは成立していません。
逆関数x=2^yはこの地点では、xとyを入れ替えただけだからです。つまり、従属変数yと独立変数xであるはずが、xとyを入れ替えただけなので、yが独立変数でxが従属変数つまり、yの値によってxが決まってしまう構造になっているためなので、f(g(x)) = x および g(f(x)) = xは成立していないんだなと。
指数関数である元の関数
y=2^x
=f(x)
とその逆関数の位置関係にある2つのグラフ(指数関数x=2^yと、対数関数y=log2(x))のうち、
指数関数で表されている
x=2^y(対数関数ならy=log2(x))
=g(x)について、元の関数t=2^xのxとtを入れ替えただけなので、さらに
逆関数にするためにyについて解くと、
y=log2(x)となります。
これは、
指数関数である元の関数
y=2^x
=f(x)
とその逆関数の位置関係(位置関係がy=xと対称であるだけで、f(g(x)=x、g(f(x))=xの検証をしていないから、正式には逆関数であるとはこの地点では言えていないから)にある2つのグラフ(指数関数x=2^yと、対数関数y=log2(x))のうち、
指数関数で表されている
x=2^yは正式には逆関数ではなかったことになります。(グラフの形は元のグラフとy=xに対して対称ですが)
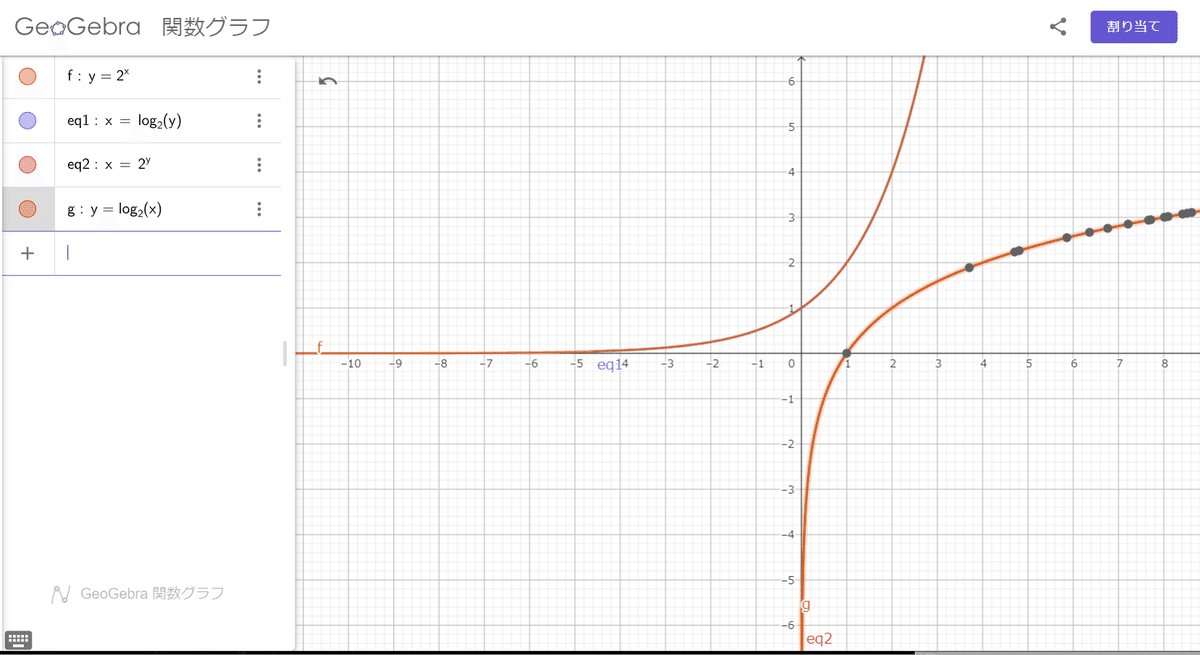
元の関数t=2^xの逆関数と同じ位置関係にあるのはx=2^tとx=log2(y)の2つのグラフがあることがわかりました。そして、x=2^tはf(g(x))=x、g(f(x))=xを満たさなかったので、元の関数t=2^xの逆関数ではないことがわかりました。
そこで、元の関数t=2^x=f(x)とy=xと対称の位置(逆関数の位置)にあるx=2^tではない、もう一方の逆関数である対数関数y=log2(x)をg(x)とすると、
t=2^x=f(x)
y=log2(x)=g(x)のとき、
f(g(x))=2^{log2(x)}
指数がlogの計算ですね。この場合、任意の変数Tとおいてから次に、両辺に、共通の「log(底:小さい因数)」をおくといいそうです。
まずf(g(x))=Tとおきます。
f(g(x))=2^{log(2)(x)}なので、Tとおくと、
2^(log2(x))=T
これは、底が2,指数がlog(2)(x)、真数がTの指数関数です。次に、
底として、小さい因数2をおいたlog(2)をつくり、両辺においたら、
log(2){2^(log2(x)}=log(2)(T)
これは、f(g(x))=2^{log(2)(x)}の右辺と、Tがlog(2)によって、真数になったことを意味しているんだと思いました。
ここで、左辺に注目です。
{2^log2(x)}
はlog(底)(真数)の形での真数部分ですが、
真数部分において、「任意の数^指数」の形、つまり真数エリアである数に指数が付いている場合、ある数についている指数部分はlogの前にもってきて、「「真数についていた指数部分」×log(底)(真数)」の形にできるそうなので、
左辺のlog(2){2^(log2(x)}で、真数部分についている指数部分とは、log(2)(x)の部分なので、これを、一番左側にもってきて、既存の左辺との掛け算にします。たとえば、log(2)(3^5)なら、5×log(2)(3)にできるというわけですね。
すると、
log(2){2^(log2(x)}=log(2)(T)は、
log2(x)*log(2)(2)=log(2)(T)となりました。
ここで、log(2)(2)というのは、対数関数で、対数関数は、指数=log(底)(真数)の形で、指数関数にすると、指数関数は、真数=底^指数でしたので、
log(2)(2)は、2=2^?となります。指数の?部分は、2の1乗が2なので、
?=1となります。指数が1だとわかったので、指数=log(底)(真数)におきかえて、1=log(2)(2)となるので、式に代入すると、
log2(x)*log(2)(2)=log(2)(T)は
log2(x)*1=log(2)(T)で、
log(2)(x)=log(2)(T)となりましたので、
両辺の真数について、x=Tとなります。
よってこれによって、もともとf(g(x))=Tと、Tをおいていたので、Tにxを代入すると、
f(g(x))=x ①
となり、逆関数の性質であるf(g(x))=xを満たしました。
逆関数のxに元の関数のyの値を入れていく形であるg(f(x))でも同様にしていきます。
元の関数がf(x)=t=2^x、その逆関数がy=log(2)(x)=g(x)、でしたので、g(f(x))は、
g(f(x))=log(2)(2^x)
先ほどとおなじようにg(f(x))=T(任意の変数)とおくと、
g(f(x))=log(2)(2^x)のとき、g(f(x))=Tとおくので、
log(2)(2^x)=T
両辺にlog(2)をおいて、両辺を対数関数における真数化にすると、
log(2){log(2)(2^x)}=log(2)(T)
左辺の真数部分は{log(2)(2^x)}です。
ここからは、少し違ってくるようです、というのは、真数部分の中で、さらにlog(底)(真数)があり、そのlogの中の真数に指数がついているからです。
この場合、真数部分のxを「真数エリアで」logの前にもってきますと、
左辺の真数部分{log(2)(2^x)}は、{x*log(2)(2)}となりました。
log(2)(2)=1でしたので(log(底)(真数)=指数において、指数関数にすると、真数=底^指数より、2=2^? ∴?=1だから)、
左辺の真数部分{log(2)(2^x)}は
log(2)(2^x)→x*log(2)(2)→x
となりましたので、
log(2){log(2)(2^x)}=log(2)(T)は、
log(2)(x)=log(2)(T)となりまして、
x=Tとなりました。
ここで、T=g(f(x))=log(2)(2^x)だったので、
x=Tなので、
x=log(2)(2^x)=g(f(x))となるので、
g(f(x))=xとなりました。②
逆関数ではy=xに対称であるほか、f(x)の逆関数がg(x)のとき、
f(g(x)) = x および g(f(x)) = x が成り立ちます。③
①②より、③を満たす(成立したので)、
f(x)=t=2^xの逆関数は、g(x)=y=log(2)(x)である
となりました。
t=2^xという指数関数では、対数関数にすると、x=log_2(t)で、グラフ上では元の関数と逆関数の位置にありますが、
「逆関数ではy=xに対称であるほか、f(x)の逆関数がg(x)のとき、
f(g(x)) = x および g(f(x)) = x が成立」
を満たさないため、
1)元の指数関数を対数関数に変化させただけの関数
2)元の指数関数のxとyを入れ替えただけの関数
これら2つの関数では、1)ではグラフは元の関数と同じ軌跡なので、グラフの形から逆関数ではありません。
2)では、グラフの形では、元の関数とy=xに対して対称なグラフですが、
「逆関数ではy=xに対称であるほか、f(x)の逆関数がg(x)のとき、
f(g(x)) = x および g(f(x)) = x が成立」
を満たさないため、元の関数の逆関数ではありません。
元の関数t=2^xの逆関数であるためには、
①y=xと対称
②逆関数ではy=xに対称であるほか、f(x)の逆関数がg(x)のとき、
f(g(x)) = x および g(f(x)) = x が成立
を満たす必要があります。そのため、元の関数t=2^xの逆関数をつくるためには、手順として、
1)xとyを入れ替える
2)入れ替えた指数関数において、指数がyになっているので、yについて解く。ここで、指数関数はy=a^xであり、aは底で固定値です。xとyを入れ替ると、x=a^yで、yについて解くと、y=log(a)(x)となります。
つまり、元の関数のxとyを入れ替えて、入れ替えた関数をyについて解くと、ここで初めて元の関数t=2^xの逆関数y=log(2)(x)となります。
逆もできる~逆関数を作る方法におけるxとyを入れ替えるタイミング
逆関数をつくるためには、xとyを入れ替えてから、その関数についてyについて解きました。こういう順番でも逆関数は作れます。
1)yについて解く
2)xとyを入れ替える
元の関数は指数関数でt=2^xであり、その逆関数は対数関数のt=log2(x)であることがわかりました。(計算過程は、①xとyを入れ替える②yについて解く もしくは、①’xについて解く ②xとyを入れ替える)
t=2^xの逆関数t=log2(x)を指数関数であらわすとx=2^t(xは真数、2は底、指数はt)です。これは何かというと、グラフでは逆関数の軌跡は描きましたが、「逆関数ではy=xに対称であるほか、f(x)の逆関数がg(x)のとき、
f(g(x)) = x および g(f(x)) = x が成立」を満たさないから逆関数ではないとなっていた指数関数のことです。
元の関数f(x)=t=2^x→x=2^t→t=log(2)(x):逆関数→ここから、この逆関数である対数関数を指数関数にx=2^t変化させると、逆関数でなくなる。
この一連からわかることは、
1)元の関数t=2^xのxとyを入れ替えた指数関数x=2^t①は、元の関数t=2^xの逆関数t=log(2)(x)を指数関数x=2^t②へ変化させたもので、このとき指数関数①=指数関数②となっている。
つまり、形だけ逆関数(なんちゃって逆関数と勝手に呼ぼうっと)である指数関数①=指数関数②であるx=2^tは、
・元の関数と逆関数をつなぐ関数(逆関数のふりをした関数で一見本物の逆関数とグラフ上では形はほぼ同じ位置にある)
・指数関数の逆関数は対数関数。このとき、逆関数である対数関数をグラフ上で表すために、指数関数化したものでもある。
というのは、元の関数→なんちゃって逆関数→逆関数→なんちゃって逆関数→xとyを入れ替える→元の関数
と言うように、なんちゃって逆関数を繋ぎ手として循環しているという感想を持ちました。
t=2^xにおいて、tの二次関数の解tが2つの正の整数解なら、xも2つの正の整数解な理由は?
元の関数t=2^xにおいて、
ⅰ) t=1のとき
t=2^xでは1=2^xで、x=0
座標であらわすと(0,1)
この逆座標は(1,0)
これをt=2^xの逆関数x=2^tに代入すると、
1=2^0で成立する。
ⅱ) t=2のとき、
t=2^xでは2=2^xでx=1
座標であらわすと(1,2)
この逆座標は(2,1)
これをt=2^xの逆関数x=2^tに代入すると、
2=2^1で成立する。
よって、t=2^xにおいて、tが正の整数ならば、逆関数x=2^yのxも正の整数となるので、t=2^xを代入したtについての方程式を解いた時のtが整数なら、xも整数となる。
と考えました。
このことをGPT-4o先生に聞いてから、OKをいただきました。それから内容をまとめてみたものを、コパイロさんに分かりやすく要点をまとめていただいたものに、どころどころ付け加えてみたものがこちらです。
t=2^xの任意の1点は、y=xに対称の逆の任意の1点になり、その1点はt=2^xの逆関数t=log2(x)上にあることになります。
ここで、(α,0)はf(t)の任意の1点で、(0、α)はf(2^x)の任意の1点で、(α、0)と(0,α)はy=xに対して対称なので、それぞれの任意の1点を表すグラフ同士もy=xに対して対称なので、2つのグラフは逆関数となるとなります。
これは、多次元方程式で、t=2^xを代入した場合のtについての二次方程式において、tが異なる2つの正の解を持つ場合、tについての二次方程式に、t=2^xの右辺2^xを代入しなおした時の、xの解も正の解だということをあらわしています。
逆関数の求め方
逆関数の求め方 関数 t = 2^x の逆関数を求める場合は、次のように進めます。
1. 元の関数を t = 2^x とする。
2. t と x を入れ替える
x = 2^t
3. これを t について解く
t = log_2(x)
したがって、t = 2^x の逆関数は t = log_2(x) です。
t = 2^x の逆関数は t = log_2(x) です。この逆関数をグラフに描くために、指数関数にすると、x=2^tで、もとのt=2^xとy = x に対称なグラフです。
つまり、t 軸上の任意の正の点 t_1 は、y=xに対して対称な逆関数上ではxの値となり、y 軸上の正の点 x_1 に対応します。これは、t が正の実数解つまり、x軸上の正の領域での任意の1点であれば、 x はy軸上で正の領域での任意の1点となるので、xもtが正の整数解ならば正の実数解(整数解)であることを意味しています。
このように、逆関数と座標を使って考えることで、方程式の解がどのようにして得られるのか、より直感的に理解することができます。数学の美しさは、このような論理的なつながりにあり、それを理解することで、数学のさらなる深みに触れることができるのです。
数学の問題を解く際には、単に解を求めるだけでなく、その解がどのようにして導かれるのか、その理由を常に考えることが大切です。そうすることで、数学の本質的な理解が深まり、より複雑な問題にも対応できるようになります。逆関数や座標を使った考え方は、その一例に過ぎませんが、数学の理解を一層豊かにするための有効なツールです。次回、方程式に取り組むときは、この視点を持って問題にアプローチしてみてください。きっと、新たな発見があるはずです。 by コパイロ先生
まとめますと、t=2^xの逆関数(t=2^x →x=2^t →t=log2(x)→x=2^t)と座標であらわせるので、元の関数t=2^xと逆関数x=2^tによって、tが正の数なら、逆関数の指数tが正の数となるので、左辺のxも正の整数になることから、tが正の整数解なら、xも正の整数解ということが、よりイメージできたということになりましたというお話でした。
この記事が気に入ったらサポートをしてみませんか?
