
MSY理論に代わる新しい資源変動の考え方
水産資源の管理はどのような考え方をもとに行われるのか、その基本的な考え方について説明します。水産資源の管理は、最大持続生産量(Maximum sustainable yield; MSY)という概念をもとに実施されています。
この持続的という概念は、現在ではごく普通に用いられる重要な概念になっていますが、水産資源の管理では、70年以上も前から、この考え方を重視していました。
しかし、概念としては正しくても、MSYをベースとした資源管理(MSY理論)は誤りであり、MSY理論に基づいて資源を管理を実行しても、資源管理の成功は期待できません。
なぜ、MSY理論が間違いであると言えるのかについて、詳しく説明するのが、この記事の目的です。さらに、MSY理論に変わる新しい資源変動の考え方も提示したいと思います。
1. はじめに
「大きく変動する資源を管理する」ということはそれほど容易なことではありません。この困難な問題を解決するためには、なぜ、資源は変動するのか、資源変動のメカニズムを明らかにしておくことが、不可欠の要件になります。水産資源を管理するときの基本的な概念として、現在、世界中で広く認められている考え方が、最大持続生産量(maximum sustainable yield、MSY)理論と呼ばれているものです。
MSY理論の概念を簡単に言うと、「平均的に資源量をある水準に維持しておけば、平均的に毎年毎年、最大の漁獲が得られる」という考え方です。逆の言い方をすると、「毎年毎年、最大の漁獲が得られるような平均的に見た場合の最適資源水準が存在する」という考え方であるとも言えます。従って、「MSY理論に基づいて資源を管理する」とは、すなわち、「その平均的に見た場合の最適資源水準に資源を維持管理すること」ということになります。
しかし、以下で詳しく述べますが、資源変動をコントロールするメカニズムとして、MSY理論は明らかに誤りであり、「毎年毎年、最大の漁獲が得られるような平均的に見た場合の最適資源水準」などは実存しません。従って、「毎年毎年、最大の漁獲が得られるような平均的に見た場合の最適資源水準に資源を維持管理する」という管理目標を設定すること自体が間違いであり、間違った資源管理目標のもとに、管理を実施したところで、資源管理に成功することはないということです。
本記事は、MSY理論が誤りであることを論証し、新しい資源変動の考え方をわかりやすく示すことを目的としました。
2. MSY理論って何?
魚などの生物資源は、自ら子(卵)を産み、再生産することができます。これが、石油や石炭などの鉱物資源と大きく異なる点です。一般に、魚はとても多くの卵を産みます。イクラはサケの卵ですが、シロサケの場合は平均的な大きさの雌1尾あたりから3000粒程度の卵が生み出されます。 太平洋クロマグロなどは成熟した雌1尾から数百万から数千万粒の卵が産出されると言われています。
しかし、孵化した稚仔魚はとても小さく、多くが他の生物によって食べられてしまい、成魚まで生き残ることができる稚仔はほんの一握りということになります。それでも、1つがいの親からは多くの次世代の親が新しく生産されることになるので、通常は、次世代の資源は増大していくことになります。その増加の仕方を仮定して導き出されたものが最大持続生産量(maximum sustainable yield、MSY)理論ということになります。
2.1 持続生産量って何?
まず、最初に、持続生産量の考え方を説明します。話を簡単にするために、スルメイカのように寿命が1年の資源を想定して説明することにします(図1)。また、図1には説明しやすいように、ロジスティックモデル(後述)と言われる最も代表的なモデルを使って、また、架空の数字を仮定して説明することにします。さらに、話を簡単にするために、1年間を1月1日から12月31日までの1年間として、話を進めます。
今、今年の1月1日に5万トンの親魚量がいたとします。その親魚量から生み出された子供が大きくなり、次の年の1月1日の親魚量(次世代親魚量)が8万トンに増加していたとします。この時、1年間に3万トンが増加したことになるので、その増加分の3万トンを漁獲しても、次の年の1月1日の親魚量は5万トンで変わりません。
その次の世代の親魚量も、5万トンの親魚量から、同様に8万トンに増大するとすれば、その次の年も、1年間に親魚量の増加分3万トンを漁獲することができることになります。この3万トンの漁獲量は、1年間に自然に増加した親魚量ですから、自然増加量と呼ばれています。また、この3万トンの漁獲量は、毎年、毎年、継続的に漁獲することができる漁獲量ということになりますから、持続生産量(または、余剰生産量)と呼ばれます。
ここで問題となるのは、親魚量が、例えば、2倍の10万トンになった場合はどうなるかということです。単純に考えると、次世代の親魚量も2倍の16万トンになるのではないかと思われるかも知れませんが、MSY理論の考え方のもとでは、そうはならず、図1に示した数値例では、16万トンより小さい14.7万トンになります(ただし、数字は架空のものです)。
なぜ2倍の16万トンにならないかと言うと、親魚量が多くなったことによって、子供の数が増え、子供同士の餌の取り合いや、生息場所の混雑等、すなわち、生存するための条件が悪化することにより、死亡率の増大や、成長率の低下などのマイナス要因が働いて、次世代の親魚量の増大が抑制されると考えられるからです。従って、この場合は、同じ量の10万トンの親魚量を次世代に残しておこうとすると、持続的に漁獲できる量(持続生産量)は、2倍の6万トンではなく、14.7万トン-10万トンの4.7万トンになります(ただし、数値は架空のものです)。

2.2 再生産関係って何?
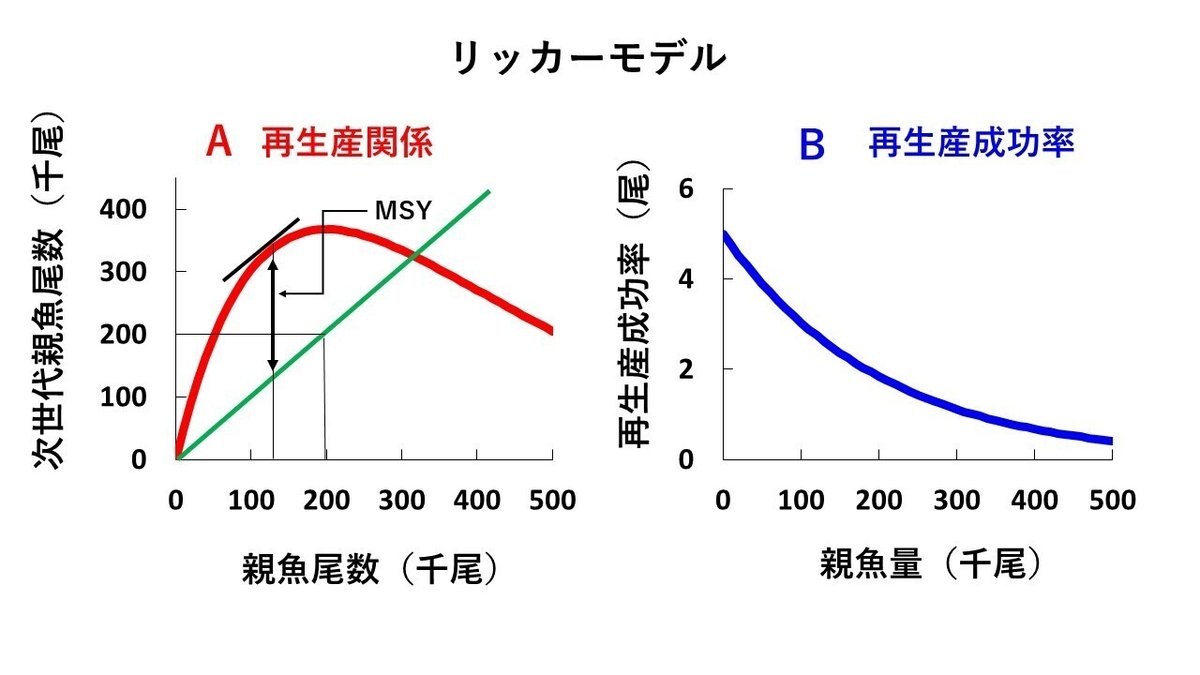
図1は、親魚量とその親魚量から再生産された次世代の親魚量との関係を図示したもので、再生産関係と呼ばれます。図1の数値例では、親魚量が5万トンの時、次世代の親魚量は8万トン、親魚量が10万トンの時、次世代の親魚量は14.7万トン、親魚量が15万トンの時、次世代の親魚量は20.2万トンになります(図1の赤の実線)。
図1の緑の実線は、上で述べたように、持続生産量を維持するために残しておくべき親魚量を示しています。赤の実線と緑の実線の差が、自然増加量(持続生産量)で、その最大値が最大持続生産量(MSY)になります。持続生産量は、図1の細い実線を上方に平行移動していって、図1の太い実線と接するところで最大になります。その時の親魚量は15万トンで、MSYは5.2万トン(20.2万トン-15万トン)になります。
2.3 余剰生産量モデルとMSYの関係
既に述べたように、持続生産量は、親魚量によって異なり、親魚量が2倍になっても持続生産量は2倍にはなりません。縦軸に持続生産量(余剰生産量)をとり、横軸に親魚量をとって図示したものが図2になります。図2は「余剰生産モデル」と呼ばれています。

図2のように図示した方が、持続生産量の最大値がどこにあるかがわかり易いと思います。当然ですが、図2でも図1と同じで、持続生産量が最大になるのは親魚量が15万トンの時で、その時の持続生産量の最大値は、5.2万トンになります。MSYを与える親魚量はMSY資源水準と呼ばれています。すなわち、「親魚量をMSY資源水準に維持しておけば、毎年、毎年、最大の漁獲が達成できる」というのが、MSY理論ということになります。
上記の説明からもわかるように、MSY理論が成立するためには、「親魚量が多くなればなるほど、餌の競合等、生存にとってマイナスとなる要因が働き、次世代の親魚量の増大を抑制するというメカニズムが存在すること(図1)」、あるいは、「持続生産量が親魚量に対して山形の曲線になるというメカニズムが存在すること(図2)」が必須の条件ということになります。
このようなメカニズムのことを「密度効果」と呼んでいます。逆の言い方をすると、「密度効果が存在することが、MSY理論が成立するための必須条件」ということになります。密度効果については、後ほど、また、詳しく説明することにします。
もし、親魚量が30万トンを超えて増大した場合は、自然増加量はマイナスとなるので、親魚量が30万トンを超えた場合は、親魚量は30万トンになるまで減少し続けます。親魚量が30万トンより小さい場合は、自然増加量はプラスですから、漁獲がなければ親魚量は30万トンになるまで増え続けます。すなわち、漁獲がない場合は、親魚量は30万トンで安定することになります。この30万トンの親魚量は、漁獲を始める以前の親魚量と考えられるので、初期資源量と呼ばれます。
3. 再生産成功率と親魚量の関係
図1の次世代親魚量(縦軸の値)を、それを生み出した1世代前の親魚量(横軸の値)で割ったものを、再生産成功率と呼んでいます。「再生産成功率」と言うと何だか難しいように思われるかも知れませんが、新型コロナウイルス感染症が拡大したとき、「再生産数」という言葉がよく使われていたことを、覚えておられる方も多いのではないかと思います。
「再生産数」とは一人のウイルス感染者が何人に感染させるかを示す数値で、「再生産数」が1未満であれば、感染は縮小に向かい、「再生産数」が1より大きいと感染は拡大していくので、感染が収束に向かうか否かを判断するために「再生産数」はよく用いられました。「再生産成功率」も名称は少し異ながりますが、同じ考え方に基づいています。
図1のロジスティックモデルの場合について再生産成功率を示したものが図3になります。図3の数値例では、再生産成功率は、親魚量が増えると直線的に減少し、親魚量が初期資源量(30万トン)のときに1になります。親魚量が30万トンより小さい時は、再生産成功率は1より大きいので、資源は増大し、親魚量が30万トンより大きい時は、再生産成功率は1より小さいので、資源は減少します。

なぜ、親魚量の増加とともに再生産成功率が減少するのか?その理由は既に述べたように、密度効果が存在するためです。逆の言い方をすると、「密度効果によって、再生産成功率が直線的に減少することを仮定したモデルが、ロジスティックモデルである」という言い方もできます。
すなわち、密度効果によって、再生産成功率がどのように減少していくと仮定するかによって再生産関係の形状(再生産モデル)が決定されるということです。例えば、鯨類資源の管理では、ペラ・トムリンソンモデルという余剰生産モデルが用いられています[1]。このモデルの再生産成功率は、ロジスティックモデルのように親魚量の増加に伴って直線的に減少するのではなく、もう少し緩やかに減少していく曲線が仮定されたモデルです(図4B)。
鯨類は哺乳類ですから、魚類に比べると生まれてくる子供の数ははるかに少なく、再生産成功率も魚類よりもはるかに小さいので、密度効果の影響は魚類ほど強くはないと考えられるからです。また、鯨類資源の場合は、親の量は重量ではなく頭数で示される点も異なります。

再生産成功率が図4Bのようなの形状の場合は、余剰生産モデルは図4Aに示したように、山の頂点が初期資源量30万頭のちょうど半分の15万頭になるのではなく、山の頂点がもう少し右の方にずれた形状になります。この場合MSY資源水準は初期資源量(30万頭)の60%の点、すなわち、18万頭になり、MSYは2500頭になります(ただし、数値はMSYは架空の値です)。
いずれにせよ、「密度効果によって、再生産成功率が親魚量の増加に対して、どのように減少していくと仮定するかが極めて重要」ということが、再生産関係を論ずるときのポイントになります。
4. リッカーが提案した再生産モデル
カナダの資源研究者であるリッカー博士は、カナダの西海岸に遡上するサケ・マス類の資源を管理するための分析を行いました。サケ・マス類は河川で産卵し、産卵を終えると死亡してしまいます。産み落された卵は、河川で孵化し、降海して成長します。成熟した個体は、生まれた河川に産卵のために回帰します。
サケ・マス類は河川に遡上してきた親魚尾数が計数されているので、リッカー博士は、そのデータを利用し、横軸にはある年に河川に遡上してきた親魚尾数をとり、縦軸には、その親魚から生まれた子供が成長し、産卵のために再び河川に遡上してきた親魚尾数の合計をプロットして再生産関係を表わし、リッカーモデルと言われる再生産モデルを提案しました(図5Aの赤の曲線)。
サケ・マス類は、海洋よりもよりもはるかに閉鎖的と考えられる河川で産卵するため、初期段階でより強い密度効果が働くと考えられます。このような事情を反映して、リッカーモデルの再生産成功率は、ロジスティックモデルのように、親魚量の増加に対して直線的に減少するのではなく、親魚量の増加に対して再生産成功率が急激に低下していく曲線が想定されています(図5B)。
親の量が20万尾の時、遡上尾数は36.8万尾で最大となり、親の量がそれ以上になると、遡上尾数は大きく減少しています(ただし、数値は架空のものです)。図5Aの緑の直線は、図2と同様で、持続生産量を維持するために残しておくべき親魚尾数を示しています。赤の曲線と緑の実線の差が持続生産量ですから、持続生産量は細い実線を上方に平行移動していって、太い曲線と接する点で最大になります。すなわち、親魚尾数が12.5万尾の時にMSY資源水準となり、MSYは21万尾になります(ただし、数値は架空のものです)。
5. それ以外の再生産モデル
既に述べた様に、再生産関係とは、ある世代の親の量と次世代の親の量の関係ですが、次世代の親の量として、どのような変数を用いるかは、魚種によって異なります。最近は、再生産関係として、横軸に親魚量をとり、縦軸に0歳魚(場合によっては、1歳魚や2歳魚)の資源尾数をとって、再生産関係を示す場合が多くなっています。従って、この場合の再生産成功率は、「親魚1㎏当りの0歳魚(場合によっては、1歳魚や2歳魚)の資源尾数」で定義されます。

リッカーモデル以外でよく使用される再生産モデルを図6Aに示しました(ただし、数値は架空のものです)。図6A はべバートン博士とホルト博士の二人の資源研究者によって1957年に提案されたモデルで、べバートン・ホルトモデルと呼ばれています。
親魚量の増大に伴う密度効果の影響で、再生産成功率は徐々に低下しますが、リッカーモデルに比べると、親魚量が大きいところでの再生産成功率の低下が少し緩やかになっている点が異なっています(図6B)。再生産成功率の曲線の形が異なることに対応して、リッカーモデルでは親魚量が大きくなりすぎると0歳魚尾数が低下してしまうのに対して、べバートン・ホルトモデルの場合は、親魚量の増大とともに、0歳魚尾数がある値に漸近していくという形状になります(図6A)。
もう1つのよく用いられる再生産モデルとしてホッケースティックモデルがあります(図7A)。このモデルは形状がアイスホッケーのスティックに似ているので、そのように呼ばれています。リッカーモデルやべバートン・ホルトモデルが提案されたのは1950年代ですから、既に、70年近くも経過しています。ホッケースティックモデルが提案されたのは、比較的最近であり、1980年代になってからです。それでも40年近く経過していることになりますが・・・。

再生産成功率でみると、ホッケースティックモデルとは、ある親魚量の値までは再生産成功率は一定で、それ以上に親魚量が増大すると、再生産成功率が親魚量に反比例して低下すると仮定したモデルです(図7B)。この場合の再生産関係は、0歳魚尾数は親魚量の増大に伴い、最初のうちは比例して直線的に増加しますが、ある親魚量水準を超えると親魚量の大きさとは無関係に、0歳魚尾数が一定値になります。すなわち、ある親魚量水準を超えると、とても強い密度効果が働くことを仮定したモデルということになります(図7A)。
ホッケースティックモデルの見た目の形状は、べバートン・ホルトモデルに似ていますが、両者には大きな相違があります。後ほど示すように、再生産関係の図を描いたとき、親魚量が増大しても0歳魚尾数がなかなか一定値に近づかないようなケースもごく普通に見られます。このようなデータにべバートン・ホルトモデルを当てはめてMSYの値を推定すると、非現実的に大きなMSYが推定されてしまうという結果になることがしばしば起こります。
しかし、MSYの値が非現実的に大きい場合は、現状のほとんどの親魚量がMSY資源水準より低くなってしまうため、乱獲状態にあると判断されてしまいます。つまり、ほとんどの親魚量水準で漁獲が許されないということになってしまいます。
ホッケースティックモデルは、ある親魚量水準以上は、強制的に0歳魚尾数を一定値に仮定してしまうので、べバートン・ホルトモデルを当てはめた時のような不都合な結果にはなりません。ホッケースティックモデルを用いれば、非現実的に大きなMSYが推定されてしまうことを避けることができるということです。
マグロ類をはじめ、多くの魚種でホッケースティックモデルが採用されるようになった本当の理由は、ホッケースティックモデルに生物学的妥当性があるからというよりも、上記のような実用上の理由によるものであると私は考えています。
換言すると、リッカーモデルやべバートン・ホルトモデルを用いてMSYを推定し、資源の管理を実施しようとするときに生ずる矛盾を覆い隠すための技術的なテクニックとしてホッケースティックモデルが考案され、クロマグロを始めとする多くの魚種で採用されるようになったということだと私は思っています。
日本のTAC対象種であるゴマサバ東シナ海系群の再生産関係でも、ホッケースティックモデルが当てはめられています。しかし、ゴマサバ東シナ海系群の再生産関係は、親魚量の増加に伴って0歳魚尾数も増加しており、0歳魚尾数が一定値になるような傾向は全く認められません。
なぜ、このような資源に対しても、強制的にホッケースティックモデルを用いるのかを水産研究機構の研究者に質問したことがあります。驚くべきことにその回答は「ホッケースティックモデルを用いないとMSYが過大に推定されてしまうから」という、上記で述べた疑念を裏付ける回答でした。
つまり、生物学的にホッケースティックモデルの方が妥当と考えられるから適用したということではなく、「ホッケースティックモデルを用いなければ、MSYを用いた資源管理ができなくなってしまうから」ということでした。これを本末転倒と言わずになんというのでしょうか?
6. 以上述べたことのポイント
以上述べたことの重要なポイントをまとめておくことにします。まず、第一は、親魚量と持続生産量の関係(余剰生産モデル)と、親魚量とその親が生産した次世代の親魚量の関係(再生産関係)とは、同じ生物現象を異なる視点から見ただけであり、資源動態という面からは、全く同じ関係性を示したものと言えます。
例えて言えば、工事中の道路などでよく見かける赤い円錐形のコーンは、上から見れば円形に見えますが、真横から見れば二等辺三角形に見えるのと似ています。観察する位置によって見える形状は異なりますが、どちらも円錐形のコーンを見ていることに変わりはありません。ここで重要なことは、図1と図2に示した様に、「MSYは余剰生産モデルを用いて定義しようが、再生産関係を用いて定義しようが、MSYに変わりはない」ということです。
第2番目の重要なポイントは、MSYは再生産関係に密度効果が存在してはじめて成立する概念であるということです。逆の言い方をすると、もし、再生産関係に密度効果の存在が認められなければ、MSYは存在せず、MSY理論の科学的正当性は破綻してしまうということです。
今後は、再生産関係に焦点を当てて、「再生産関係に密度効果の存在が認められるか否か」という視点から、MSY理論の妥当性について議論することにします。
7. 密度効果って何?
以上の議論から、資源の変動メカニズムについて議論する場合、密度効果という概念の妥当性が極めて重要なポイントであることがわかると思います。この節では、密度効果について、少し詳しく説明する事にします。 密度効果とは何か? 世界大百科事典第2版では以下のように、密度効果を説明しています。
「一般には,個体群の密度によって個体の産子数,成長率,死亡率,行動などに変化が生じ,ひいては個体群増加率に影響が表れることをいう。とくに高密度化での密度効果を〈混み合い効果crowding effect〉と呼ぶこともある。空間や食物という資源には限りがあるから,生物がその個体数を無限に増加させることは不可能である。このため人口(個体数)は,最初のうちは幾何級数的に増えるが,やがて上限に達して横ばいになってしまう。」ただし、ここで個体群とは、ある場所または地域に住んでいる生物の同種個体の集まりを言う。
この説明を読んで、密度効果の存在に疑問を持つ人はいないだろうと思います。なぜなら、密度効果は我々の経験や感覚などともとてもよく一致する概念だからです。例として、プランターなどでミニトマトを育てる場合を考えみましょう。3本程度の苗を植えるのが最適と思われる大きさのプランターに、30本も苗を植えてしまうと、苗は十分に大きく育つことができず、ミニトマトもあまり実らないことは、誰もがよく知っていることだと思います。苗を大きく育てるためには、苗一本当たりの面積を十分に確保してやる必要があるからです。このような密度効果の存在を示す例はとても多いと思います。
大腸菌やミジンコの個体数が増加する様子を調べる試験管での観察や水槽実験などを行って、ロジスティックモデルが良く当てはまることを、すなわち、個体数の変動が密度効果によって調整されることを示した実験などもよく知られています。上記以外でも、ロジスティックモデルが当てはまるという実験結果の例は多くあり、ロジスティックモデルを魚の資源変動のメカニズムとして適用することに何ら疑問を抱かない資源研究者は、実はとても多くいます。
しかし、条件を一定にした実験室の中での個体数変動のメカニズムと、環境条件が時々刻々大きく変わる広大な海の中での魚の個体数変動のメカニズムが同じであると見なすのは、どう考えてもかなり無理があると言わざるを得ません。密度効果は、それこそ密度がとても重要なわけですから、生物個体1個体が利用できる資源という観点からの、もっと厳密な議論が必要なはずですが、実際には感覚的な議論に終始してしまっているのが実状です。
先ほどのプランターの例で言えば、プランターの大きさが、10倍になれば、苗を10倍の30本植えても、密度効果は起こらないし、植える苗の数を3分の1にしたところで、プランターの大きさが、10分の1になってしまったとすれば、苗は大きく成長することはできなくなります。すなわち、上記の例では、プランターの大きさを固定して考えてしまっているところに、致命的な論理的欠陥があるということです。
実際には、プランターの大きさが、時々刻々変化することはありえませんが、海の中では、環境が時々刻々大きく変化しており、プランターの大きさが、時々刻々10倍になったり、10分の1倍になったりするような状況が、ごく普通に起こっていると考えなければならないということです。私は「密度効果も環境変動によって起こる」と考えるべきであると思いますが、そのことはまた、9節でマイワシの再生産関係を例に説明することにします。
8. 再生産モデルの妥当性について
さて、基本的な準備が整ったので、以下に私がMSY理論が誤りであると主張する根拠を示したいと思います。まず、上で述べた再生産モデルの妥当性について議論することにします。
8.1 否定根拠1 ー 再生産モデルを支持するデータがない ー
1995年にマイヤーズ達は世界の漁業資源の再生産関係において密度効果が認められるか否かを調べました。その結果は、「調査した128系群中、密度効果が認められたのは、サケ類2種と大西洋ニシンのたったの3魚種のみであった」という驚くべきものでした。
ここで、系群とは、分布域などが異なる資源変動の単位となる集団のことをいいます。同じ魚種でも、いくつかの系群に分かれていて、それぞれ別々に資源分析が行われるのが普通です。例えば、日本周辺のマイワシも、マイワシ太平洋系群とマイワシ対馬暖流系群に分けられており、それぞれ別々に資源分析が行われます。
マイヤーズらが論文を発表してから20年以上の歳月が経過した2015年、シュワルスキー達は、224系群にもおよぶ魚の再生産関係を調べ、その結果を発表しました。その内容もまた驚くべきもので、彼らが調べた224系群中のなんと84%以上の系群で、3つの再生産モデル(リッカーモデル、べバートン・ホルトモデル、ホッケースティックモデル)ではその変動が説明できないことを示しました。また、同時に加入量の変動要因としては環境変動の方が親魚量の大きさよりもはるかに大きいことも示しました。
ただし、ここで加入量とは、0歳の資源尾数とか1歳の資源尾数のことを指します。魚種・系群により、推定されている資源の最小年齢が異なるため、何歳の資源尾数を加入量とするかは魚種・系群によって異なるためです。
すなわち、マイヤーズ達とシュワルスキー達の2つの研究は、「密度効果を仮定して導かれた上記3つの再生産モデルにあてはまる実際のデータはほとんどない」という驚くべき事実を、多くの実データを分析することによって明らかしたことになります。シュワルスキーらが検討した224系群の再生産関係の図はすべてインターネット上に公開されているので、誰でも見ることができます。実際に見ていただくのが一番いいと思いますが、例として、3つの代表的なパターンを図8に示しました。

図8Aは、224系群中の23番目に掲載されている東ベーリング海のスケトウダラの再生産関係です。ここで環境が同じと見なせる年は同じ色で示されています。図8Aで、緑の丸で示した年は全体的に加入量が大きく、また、オレンジ色の丸で示した年は、全体的に加入量が小さいことがわかります。すなわち、加入量の大小は親魚量ではなく、環境による影響の方がはるかに大きいことを示しています。
図8Aの実線は、データにあてはめたリッカーモデルを、破線はべバートン・ホルトモデルを示しますが、当てはまりがいいなどとはとても言える代物ではありません。加入量が親魚量の増大に伴う密度効果によって頭打ちになるというような傾向は全く認められず、どちらかというと全体的な傾向としては増加傾向にあるように見えます。今後、このようなパターンを「増加」と呼ぶことにします。
図8Bは、224系群中の16番目に掲載されている東ベーリング海のマダラの再生産関係を示します。実線はデータにあてはめたホッケースティックモデルを、破線はリッカーモデルを示しますが、このケースも当てはまっているなどとはとても言えないレベルの図ということがわかります。
このケースでは、使用されたデータの期間内では環境は同じですから、この例の場合は、環境変動が加入量に及ぼす影響は無視できると考えてもいいでしょう。従って、もし密度効果があるのであれば、大きな資源のところで、きれいな頭打ちや低下の傾向が認められてもいいはずです。しかし、点は全体的に大きくばらついていて、加入量と親魚量の間にはいかなる関係も認められません。今後、このようなパターンを「無相関」と呼ぶことにします。
図8Cは、224系群中の20番目に掲載されているアラスカ湾のナメタガレイの再生産関係を示します。実線はデータにあてはめたホッケースティックモデルを、破線はリッカーモデルを示しますが、特に、ホッケースティックモデルなどは、当てはまっているなどとはとても言えた代物ではないことがわかります。
しかし、この図を見て、「親の量が多いところでは、リッカーリモデルがよくあてはまっているんじゃないか」などと思う人がいるかも知れませんが、決して、そんな見方をしてはいけません。なぜなら、「統計学で何かを語ることができるのはデータがある範囲に限る」というのが、統計学の基本中の基本だからです。データがない領域のデータを仮定して、何かを判断することは許されていません。
図8Cは、親魚量が多いところしかデータがなく、親魚量が中ぐらいのレベルの時や、親魚量が小さいレベルの時のデータは全くありません。このような全くデータがない領域も含めて「リッカーモデルが当てはまるだの、ホッケーステックが当てはまる」などという議論は意味がありません。このデータから言えることは、「データが存在する範囲においては、親が多いほど子が少ないという傾向がありそうだ」ということだけです。今後、このようなパターンを「減少」と呼ぶことにします。
このような「親が多いほど子は少ない」というデータしか得られない魚種があるということは、生物学的にはとってもおかしいことですよね。しかし、このようなパターンは、たまたま偶然に出現したものではなく、ある一定の割合で必ず出現する点に注目する必要があると思います。
シュワルスキーらが示した再生産関係の図では、224系群中15%ぐらいはこのような減少するパターンを示します。このような傾向が、必ず、一定の割合で出現するということは、たまたま偶然にそのような傾向が現れたというよりは、「そのような傾向が出現する何らかのメカニズムが働いている」と考えた方が合理的でしょう。
以上の分析結果から言える極めて重要なことは、「現在、資源管理に使用されている再生産モデルに合致する実際のデータはほとんどない」ということであり、このことから言えることは、「密度効果を重視した再生産モデルは、実データによる裏づけのない架空のものにすぎない」ということです。さらに言えることは、「架空の再生産モデルから導き出されたMSY理論もまた、架空のものでしかない」と言うことです。
8.2 否定根拠2 ー密度効果の存在を示す分析方法が誤っているー
再生産関係に密度効果が認められないと私が主張する第二の根拠について述べます。再生産関係に密度効果が認められるという主張は、次のような分析結果をもとにしている場合がほとんどです。すなわち、縦軸に再生産成功率をとり、横軸に親魚量をとってプロットすると、明らかな減少傾向が認められることを示し、「このような再生産成功率の減少傾向が現れるのは、密度効果が存在するからである」と結論づける場合が多い。
しかし、この分析には、根本的な誤りがあります。そのことを、簡単な数値例を用いて説明することにします(図9)。話を簡単にするために、3年間の再生産関係のデータがある場合を考えます。また、分かり易くするために、少し極端な数値例を使って説明することにします。
たまたま3年間、親魚量は50トン、0歳魚尾数は10万尾で一定であったとします。従って、再生産成功率は100,000尾÷50,000kgで計算されるので、親魚量1kg当り2尾となり、3年間、同じ値です。ところが、3年間のうち2年間で推定に誤りがあり、ある年は誤って親魚量を25トンと過小評価してしまい、また、ある年は、親魚量を100トンと過大推定してしまったとします。この時、再生産成功率はどのような値になるでしょうか?

話を簡単にするために、0歳魚尾数には誤差がないとすると、親魚量を過小推定した年の再生産成功率は100,000尾÷25,000kgで計算され、1kg当り4尾となります。また、親魚量を過大推定した年の再生産成功率は100,000尾÷100,000kgで計算され、1kg当り1尾となります。残りの1年は、親魚量には推定誤差がないので、再生産成功率は正しく1kg当り2尾と計算されます。そのようにして求めた3年間の再生産成功率を親魚量に対してプロットすると、図9が得られます。
計算された再生産成功率は明らかな低下傾向を示すことがわかります。このような傾向は、より現実的な場合を想定した、すなわち、推定誤差の大きさがもっと小さい場合や、0歳魚尾数にも推定誤差がある場合、データの数がもッと多い場合でも同様に認められることが、既に、シミュレーションを実施して確かめられています(参考文献2)。
一般的に言えば、「観測値Aを観測値Bで割ったものを縦軸にとり、その分母である観測値Bを横軸にプロットすると、観測値Bに内在する観測誤差によって、必ず、見かけ上の低下傾向が表れる」ということです。その原理は、図9で説明した通りです。 すなわち、親魚量に推定誤差がある場合、再生産成功率を親魚量に対してプロットすると、密度効果が存在しなくても、必ず、低下傾向が認められるということです。このことは、「再生産成功率を親魚量に対してプロットした時に、低下傾向が認められること」、イコール、「密度効果が存在すること」ではないということを示しています。
9. マイワシの再生産関係について
9.1 マイワシの0歳魚尾数と親魚量の経年変動
図10は、マイワシ太平洋系群の0歳魚尾数(対数値)と親魚量(対数値)の経年変動を示したものです。対数値とは、対数変換した値のことで、変動が大きいデータ、例えば、数百の値をとる年と、数百万の値をとる年等が混在するようなデータを図示すると、小さい値の変動は、ほとんど0と区別がつかず、小さい値の変動の様子がよくわかりませんが、対数値に変換して図示すると、全体的な変動の様子がよくわかるので、対数値に変換して図示した方がいい場合もよくあります。
図10で、丸と実線で示したものは毎年の値を、ピンクの実線は3年移動平均を示します。ここで、3年移動平均とは、ある年の前後1年間、すなわち、計3年間の平均を計算し、その年の値としてプロットした図です。例えば、1959年、1960年、1961年の0歳魚尾数の平均値を1960年の0歳魚尾数の値としてプロット、1960年、1961年、1962年の0歳魚尾数の平均値を1961年の0歳魚尾数の値としてプロットする、といった操作を、順番に行っていった図ということです。毎年、毎年、大きく変動するようなデータを滑らかにして表示し、大まかな変動の傾向をつかみたいような時によく使用します。

図10Aの丸と実線で示したものは、マイワシ太平洋系群の0歳魚尾数(対数値)の経年変動ですが、毎年、毎年、大きく変動していることがわかります。図10Aのピンクの実線は、その3年移動平均をとったものですが、毎年の変動に比べると、変動は滑らかになっていることがわかります。
図10Bは、マイワシ太平洋系群の親魚量(対数値)の経年変動ですが、親魚量の方は、毎年の年変動そのものが小さいので、3年移動平均をとっても、毎年の変動とあまり変わらず、丸と実線で示した変動とピンクの実線はほとんど一致していることがわかります。
図10Aと図10Bのピンクの実線同志を比べると、親魚量の変動パターンは、0歳魚尾数の変動パターンをそのまま2-5年、右方向にずらしたようなパターンになっていることがわかります。2-5年のずれは、マイワシの平均的な成熟年齢に相当すると考えられるます。
このような傾向は、他の魚種、系群についても一般的に認められます。このような現象は、資源変動のメカニズムを考えるときに極めて重要なポイントになるのですが、そのことについては、また、後ほど説明する事にします。
9.2 マイワシの再生産関係
図10Aの横軸に平行に引いた実線は、0歳魚尾数の全期間の平均値を示します。マイワシ太平洋系群の0歳魚尾数の経年変動は、青色で示したように、0歳魚尾数がこの平均値よりも低い期間(低水準期と呼ぶことにします)、赤色で示したように、0歳魚尾数がこの平均値よりも高い期間(高水準期と呼ぶことにします)、緑色で示したように、0歳魚尾数がこの平均値の前後を変動している期間(中水準期と呼ぶことにします)、の3つの期間に分けることができます。
図10Bに示した親魚量の経年変動についても、2-5年程度右にずれていますが、0歳魚尾数の経年変動と、ほぼ同様のことが言えます。すなわち、親魚量の経年変動についても、青色で示した低水準期、赤色で示した高水準期、緑色で示した中水準期の3つの期間に区分することができます。従って、再生産関係においても、0歳魚尾数、親魚量ともに低水準にある低水準期、0歳魚尾数、親魚量ともに高水準にある高水準期、0歳魚尾数、親魚量ともに中水準にある中水準期の3つの期間に区分可能だと思われます。
図11は、マイワシ太平洋系群の再生産関係を示したものです。予想通り、青色で示した低水準期、赤色で示した高水準期、緑色で示した中水準期の3つの期間に分かれていることがわかります。しかも、それぞれの3つの期間内で、点の軌道は時計回りのループを形成していることもわかります。
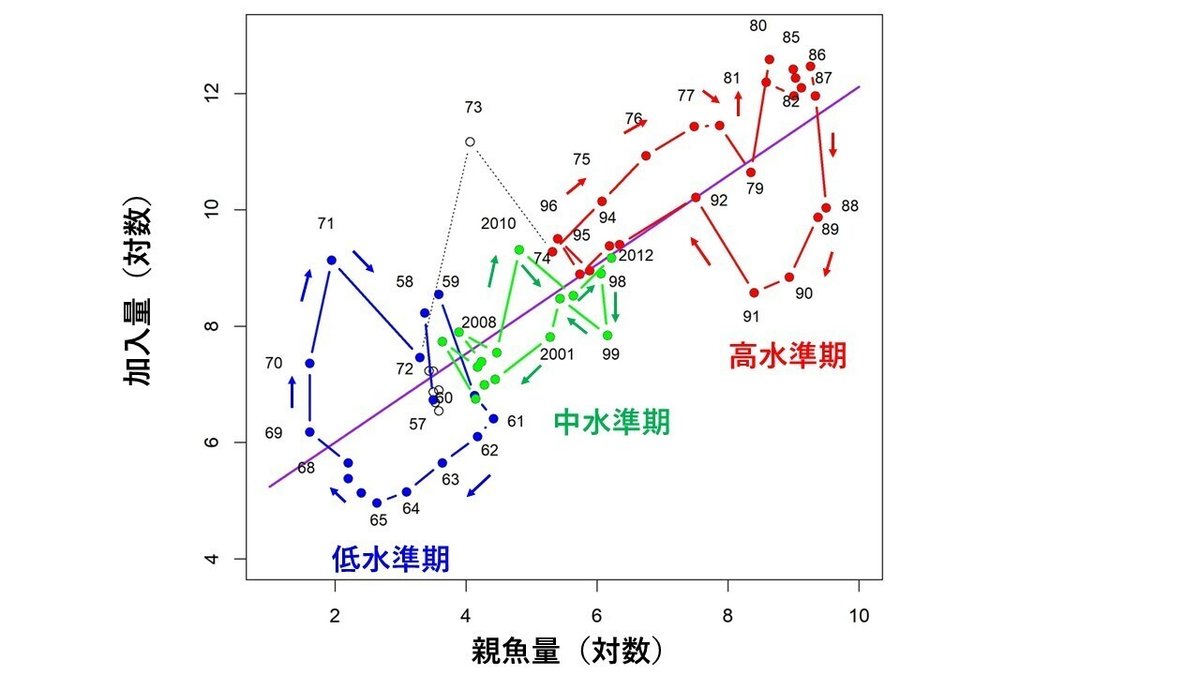
9.3 否定根拠3 ーマイワシの再生産関係は「密度効果の存在を仮定して導出された再生産関係が誤りであること」を示している
説明をわかりやすくするために、図11に示したマイワシ太平洋系群の再生産関係を模式的に示したものが、図12になります。図12は、(1)マイワシの再生産関係は低水準期、高水準期、中水準期の3つのグループに分けられること、(2)それぞれの期間内において、時計周りのループが認められること、を模式的に示したものです。

図12を見ると、赤色の上向きの矢印で示したように、0歳魚尾数が急増している時期が3回あります(その時の親魚量を図中のA、C、E で示しました)。同様に、太い青色の下向きの矢印で示したように、0歳魚尾数が急減している時期も3回あります(その時の親魚量を図中のB、D、F で示しました)。
すなわち、高水準期で0歳魚尾数が急増している時の親魚量Eは、中水準期で0歳魚尾数が急減している時の親魚量Dよりも大きいことがわかります。また、中水準期で0歳魚尾数が急増している時の親魚量Cは、低水準期で0歳魚尾数が急減している時の親魚量Bよりも大きいことがわかります。
親魚量Eで0歳魚尾数が急増し、それより低い親魚量Dで、0歳魚尾数が急減する現象は、もし、密度効果によって0歳魚尾数が増減しているという考え方が正しいのであれば、決して起こらないはずです。すなわち、マイワシの再生産関係は、0歳魚尾数の増減が密度効果によって起こるという考え方が誤りであることを示しています。このことが、密度効果を重視した再生産関係が誤りであると私が主張する第3の根拠です。
10. マイワシのような再生産関係が生じるメカニズム
現在用いられている密度効果の存在を前提とした再生産モデルでは、図11に示した様なマイワシの再生産関係が出現するメカニズムを説明することは不可能です。それではいったい、どのようなメカニズムによって、マイワシの再生産関係のようなパターンが出現するのでしょうか?
そのメカニズムを考えるために、まず、最初に、これまで述べてきた議論を整理しておきたいと思います。現行の資源変動理論(MSY理論)と新しい資源変動の考え方の相違は、「資源変動の主要因として、密度効果を重視するか否かの違い」ということになります。
現行の資源変動理論は「再生産成功率は密度効果によって、すなわち、親魚量の水準によって決定される」と考えるのに対して、新しい資源変動の考え方では、「再生産成功率の大小は親魚量の水準ではなく、環境変動によって決定される」と考える点が大きく異なっています。
現行の資源変動理論(MSY理論)を支持する資源研究者たちは、「現行のMSYは、環境変動の影響も考慮されており、古典的なMSYの考え方とは異なる」と主張しますが、彼らの言う「環境変動を考慮する」とは、まず、リッカーモデルやホッケースステックモデルなどによって0歳魚尾数決定され、その値が環境変動の影響で多くなったり、少なくなったりするという考え方を意味しています。
すなわち、環境変動はリッカーモデルやホッケースステックモデルなどによって決定された値を上下にばらつかせる役割をしているだけであり、「環境変動が再生産成功率を決定する主要因である」とは決して考えていません。従って、平均的に見れば、従来のMSYの考え方と全く変わっていない、ということになります。
10.1 密度効果も環境変動によって生じる
新しい資源変動の考え方では、「密度効果は資源変動の主要因でない」ことはもちろんのこと、「密度効果自体も環境変動によって生じる」という考え方をします。このことは、極めて重要なポイントですので、以下で少し詳しく説明しておきたいと思います。
環境がいい状態が永遠に続くわけでもないし、環境が悪い状態が永遠に続くわけでもありません。環境がいい状態がしばらく続くと、必ず、環境が悪い状態がやってきます。 図13は、環境が周期的に変わる例として、環境がいい状態が3年続き、その後に、環境が悪い状態が3年続き、・・・という状態が繰り返されている場合を想定し、図示したものです。

再生産成功率の高低は環境によって決定されるとすると、環境がいい状況下では再生産成功率は高く、0歳魚尾数は増え続けます。しかし、やがて突然に、環境が悪い状態がやってきます。環境が悪くなり、例えば、餌の量が1/10になってしまったとすると、そこで激しい密度効果が発生することになります。再生産成功率は激減し、魚体の平均体重も減少することになります。
環境が悪い状態になる前は、環境がいい状態が続いていたわけですから、環境悪化が起こる時は必ず、資源水準はそれまでの数年間と比べると高いはずです。つまり、再生産成功率の減少や魚体の平均体重の減少は、それまでの数年間と比べると、必ず、資源水準が高い時に起こるということです。図12の親魚量水準が、B、D、F がそれに相当します。
反対のケースも同じです。環境が悪い状態が続いていたとします。0歳魚尾数は毎年減少し続け、資源量は低水準になっています。しかし、悪い環境状態が永久に続くわけではないので、必ず、環境がいい状態に変化します。
環境がいい状態に変化すると、再生産成功率は上昇し、魚体の平均体重なども増大します。従って、それまでの数年間を比べると、再生産成功率は上昇し、魚体の平均体重なども増大します。その結果、それまでの数年間を比べると、再生産成功率は上昇し、魚体の平均体重なども増大します。
すなわち、再生産成功率の上昇や、魚体重の増加は、それまでの数年間と比べると、必ず資源水準が低い状態の時に起こることになります。図12で示した親魚量水準で言うと、A、C、E がそれに相当します。
これが資源水準の高い時に再生産成功率や平均体重の低下が起こり、資源水準の低い時に再生産成功率や平均体重の増大が起こる「カラクリ」です。
換言すると、横軸に資源水準をとり、縦軸に再生産成功率や平均体重をとった時に減少傾向が認められるのは、密度効果によるものである、と主張するのは誤りということになります。多くの資源研究者がこのことに気付かず、みかけの現象だけに囚われているということです。
図12に示したように、低水準期は低水準期で、中水準期は中水準期で、高水準期は高水準期で、上記のことが起こるので、結果として図12で示したマイワシの再生産関係のような、パターンが生じるということです。
11. TAC対象種の再生産関係に認められる3つのパターンと軌道の移動方向
既に述べたように、図8は、再生産関係に見られる3つのパターン、増加、無相関、減少を示す実例を示したものです。シュワルスキーらが示した224系群中15%程度が減少するパターン、15%程度が増加するパターン、残りの70%程度が、無相関と考えられるパターンになります。このような3パターンは、日本沿岸のTAC対象種でも、同様に観察されます。
スケトウダラ日本海北部系群は推定が可能な資源尾数の最小年齢が2歳であるので、再生産関係は、2歳魚資源尾数を加入量として親魚量に対してプロットして示されています。図14の左の図はスケトウダラ日本海北部系群の再生産関係を示します。また、右の図は再生産関係を年代順に線で結んだものを示します。ただし、親魚量と2歳魚資源尾数は5年移動平均とった値です。図中の数字は年を示します。

3年移動平均については、既に説明しました。3年移動平均は前後1年間の計3年間の平均を使いますが、5年移動平均は、ある年の前後2年間(計5年間)の平均を、その年の値として用いる点が異なります。平均する年数を多くすればするほど、より滑らかな軌跡になります。
図14の左の図をみると、スケトウダラ日本海北部系群の再生産関係は、親魚量の増加に対して加入量も増加する傾向(増加傾向)を示すことがわかります(統計的検定を行うと、当てはめた直線の傾きは正とみなされます。すなわち、統計的に増加傾向があると判断されます)。
また、図14の右の図をみると、最後の2004年から2015年の12年間は反時計回りを示しますが、それ以前の1986年から2003年までの17年間は、時計回りを示しています。従って、全体的には時計回りがやや卓越している、と考えてもいいでしょう。
スケトウダラ太平洋系群は推定可能な資源尾数の最小年齢が0歳ですから、再生産関係は、0歳魚資源尾数を加入量とし、親魚量に対してプロットしたもので表示されます。図15の上段左の図はスケトウダラ太平洋系群の再生産関係を、上段右の図と下段の2つの図は、5年移動平均をとったときの再生産関係を、期間別に示したものです。

図15の上段左の図をみると、スケトウダラ太平洋系群の再生産関係は、親魚量の増大に伴って加入量が減少することがわかります(統計的検定を行うと、当てはめた直線の傾きは負と見なされます。すなわち、統計的には加入量は親魚量の増大に伴って減少傾向があると判断されます)。
また、図15の上段右の図をみると、1983年から1991年までの9年間は反時計回り、下段の2つの図をみると1991年から1998年までの8年間と、1998年から2012年までの15年間は時計回りの軌跡を、2012年から2015年までの4年間は、反時計回りの軌跡を描くことがわかります。従って、スケトウダラ太平洋系群の再生産関係は減少傾向を示し、全体的には時計回りの軌跡を描く場合が卓越すると考えてもいいでしょう。
ゴマサバ太平洋系群は推定可能な資源尾数の最小年齢が0歳ですので、再生産関係は、0歳魚資源尾数を加入量として、親魚量に対してプロットしたもので表わされます。図16の左の図はゴマサバ太平洋系群の再生産関係を、右の図はその5年移動平均をとって、年代順に結んだものです。
図16の左の図をみると、ゴマサバ太平洋系群の再生産関係は、増加傾向も減少傾向も認められず、全体的に大きくばらついていて、無相関と見なせることがわかります(統計的検定を行うと、当てはめた直線の傾きは0と見なされる。すなわち、統計的には加入量と親魚量とは無相関と判断されます)。また、図16の右の図をみると、ゴマサバ太平洋系群の再生産関係は時計回りの軌跡を描くことがわかります。
日本沿岸のTAC対象種も、シュワルスキーらが示した再生産関係と同様に、増加、無相関、減少の3つのパターンが出現することがわかりました。
また、上記に示した3系群の場合は、すべての系群で時計回りの軌跡が卓越することもわかりました。

スケトウダラ日本海北部系群の再生産関係は傾きが正で、スケトウダラ太平洋系群のそれは傾きが負となります。同じ魚種であり、また、北海道の太平洋側と日本海側ですから、緯度的にも近い海域に生息しているにも関わらず、なぜ、2つの系群で再生産関係の傾きが全く逆のパターン示すのか、従来の密度効果に基づく再生産関係の考え方では、到底説明することなどできないでしょう。
12. クロマグロの再生産関係に出現する3つのパターンと軌跡の方向
実は、このような例は、日本のTAC対象種の再生産関係だけではなく、クロマグロでも認められています。図17は、太平洋クロマグロ、大西洋クロマグロ西系群、大西洋クロマグロ東系群の再生産関係を示したものです。
太平洋マグロの再生産関係のばらつきは極めて大きく、ゴマサバ太平洋系群同様、親子関係は全く認められないことがわかります。これに対して、大西洋クロマグロ西系群の再生産関係は、増加傾向を、大西洋クロマグロ東系群の再生産関係は減少傾向を示していることがわかります。

では、ループの向きはどうなるでしょうか? 図18は太平洋クロマグロの再生産関係について、5年移動平均を計算し、わかりやすいように、3つの期間に分けてループの向きを示したものです。
図18aは1954年から1968年まで(15年間)、図18bは1969年から1990年まで(22年間)、図18cは1991年から2014年まで(24年間)を示します。いずれの期間でも、反時計まわりの軌跡を描くことがわかります。すなわち、太平洋クロマグロの再生産関係は無相関で反時計回りのループを描くことがわかります。

図19は、大西洋クロマグロ西系群について、5年移動平均を計算し、再生産関係を示したものです。大西洋クロマグロ西系群は親魚量と加入量が大きく変動しているので、さらに対数変換をして再生産関係を示ました。

図19aは全期間を示します。図19bは、1972年から1988年までの17年間を示しますが、この期間は時計回りをしています。1989年から1998年までの10年間(図19c)は反時計回りを示しますが、1999年から2008年までの10年間(図19d)は再び時計回りを示すことがわかります。従って、大西洋クロマグロ西系群の再生産関係は、傾きが正で全体的には時計回りと判断することができます。
図20は、大西洋クロマグロ東系群について、5年移動平均を計算し、再生産関係を示したものです。1970年から1993年までの24年間(図20a)、及び、1993年から2005年までの13年間(図20b)のいずれの期間も、時計回りとみなされます。すなわち、大西洋クロマグロ東系群の再生産関係は、傾きが負で時計回りと判断することができます。

一般に、成熟年齢は乱獲が進むと、若齢化することが知られていますが、それほど大きな変動とは思われませんし、また、年代による変動もそれほど大きいとは考えられません。それに対して、環境変動の周期の方は、海域によっても、年代によっても大きく変わるものと考えられます。ある年代は周期が20年程度と長い場合もあれば、ある年代では、5年とか10年とかの短い周期で環境が変動するというように、時期による大きな相違は、しばしば見られる現象です。
次節で説明しますが、再生産関係の軌道が、時計回りを示すか、反時計回りを示すかは、環境変動の周期の長さと、成熟年齢の大きさとの相対的な関係によって決まると考えられます。従って、同じ系群であっても、年代によって、時計回りを示す場合や、反時計回りを示す場合など、両者が混在する場合があったとしても、十分にあり得る現象ではないかと思います。
このことは、資源変動に大きな影響を与えていると考えられる主要な環境要因の周期についても、系群ごとに詳細な分析を行い、時計回りを示すか、反時計回りを示すかの対応関係を、注意深く調べる必要があることを示しています。
しかし、実際には、環境変動と加入量変動との関係について、詳細な分析が行われている系群はほとんどないので、当面の分析方法としては、とりあえず、どちらの傾向がより卓越しているかによって、全体的な軌跡の方向性を判断することにしました。しかし、このような分析だけで十分であるという訳では、もちろんありません。系群ごとに、環境変動の周期も考慮した、さらなる分析が必要であることは言うまでもありません。
いずれにしろ、以上の分析から再生産関係として、増加、無相関、減少の3つのパターンが出現すること、また、再生産関係の点を年代順に結んでいくと、時計回り、反時計回りの軌跡が現れることわかりました。
13. 再生産関係に6つのパターンが出現するメカニズム
これまでの議論で、再生産関係には、増加、無相関、減少の3つのパターンが出現すること、また、再生産関係の点を年代順に結んでいくと、時計回り、反時計回りの軌跡が現れることがわかりました。すなわち、再生産関係は3つのパターンそれぞれに対して、時計回りと反時計回り2つのケースがあるので、計6パターンに分類可能であることがわかりました。本節では、なぜ、そのような6つのパターンが出現するのか、そのメカニズムについて説明したいと思います。
13.1 シミュレーションを行うための仮定
図10に示したマイワシの0歳魚尾数や親魚量の経年変動をみると、0歳魚尾数は環境変動の影響により周期的に変動し、親魚量は、成熟年齢分、右方向にずれて、0歳魚尾数と同様の周期的変動をしていることがわかります。そこで、上記のような状況を想定したシミュレーションを実施することにします。
すなわち、(1)0歳魚尾数は環境変動により周期(T)の周期変動をし、(2)親魚量は成熟年齢分、右方向にずれて、0歳魚尾数と同様の周期変動をする場合を想定します。
図21はシミュレーションで用いる0歳魚尾数(赤丸)と親魚量(青丸)の経年変動を示したものです。ここで、0歳魚尾数は環境変動の影響により、周期8年の周期変動しているものとします。
他の周期、10年とか15年とかを仮定しても、定性的な結論は同じです。成熟年齢については、例として成熟年齢が5歳の場合について説明しますが、成熟年齢が0歳、1歳、・・・、の場合も、全く同様の議論が可能です。
図21で、0歳魚尾数aは、成熟年齢に相当する5年、右方向にずれて親魚量Aになります。同様に、0歳魚尾数bは5年後に親魚量Bになります。すなわち、0歳魚尾数の曲線をそのまま5年分、右方向にずらしたものが親魚量を表す曲線になります。

実際には、0歳魚尾数は尾数であり、親魚量は重量ですから、それぞれY軸の値が異なりますが、話を簡単にするために0歳魚尾数と親魚量のY軸の値が同じになるように調整して示してあるものとします。例えば、親魚量が50万トンで、0歳魚尾数が300万尾の年、親魚量が100万トンで、0歳魚尾数が600万尾の年、・・・、等の場合は、0歳魚尾数を6で割った値をプロットすると、同じy軸の目盛りを使って表示することができます。
13.2 なぜ、再生産関係が減少傾向で、反時計回りのループを示す場合が出現するのか?
図22に示したように、1周期8年間は親(親魚量)と子(0歳魚尾数)の増減の組み合わせによって、4つの期間に分けられることがわかります。①の期間では、子は減少し、親は増加、②の期間では、子も親も増加、③の期間では、子は増加し、親は減少、④の期間では、子も親も減少しています。

①の期間では、子は減少し、親は増加していますが、このような場合に、再生産関係を表すグラフ上にある一点が、次の年にはどちらの方向に移動するかを考えます。
わかりやすいように、図23は数値を入れて説明しています。図23①は、例えば、ある年の親魚量が50万トンで、0歳魚尾数が300万尾であったとします。それが、次の年には、親魚量が70万トンに増加し、0歳魚尾数が280万尾に減少していたとします。この場合は再生産関係を示すグラフ上にプロットされた点(50, 300)は、次の年には右下の方向の点(70, 280)に移動します。

図22下段①の図もそれと同じ状況を表していています。すなわち、0歳魚尾数は減少、親魚量は増加ですから、次の年には点は太線の矢印で示した右下の方向に移動します。ただし、①の期間は、その状態が3年間続くので、長い矢印で示してあります。
図22の期間②は、0歳魚尾数も親魚量も増加する場合です。この場合の数値例を図23の②に示しました。例えば、ある年の親魚量が70万トンで、0歳魚尾数が280万尾だとします。それが、次の年に、親魚量が90万トンに増大し、0歳魚尾数も300万尾に増大していたとします。
この場合は再生産関係を示すグラフ上にプロットされた点(70, 280)は、次の年には右上の方向の点(90, 300)に移動します。図22の下段②の図は、その様子を示していて、この②の期間では、次の年には点は太線の矢印で示した右上の方向に移動します。
ただし、②の期間は、その状態が続くのは1年間だけですので、短い矢印で示してあります。矢印の長さは期間の長さに比例して長短が描かれていますので、①の期間は3年、②の期間は1年間ですから①の方の矢印は長く、②の方の矢印は短く描かれているということです。
図22の③、④についても同様です。③の期間では親は減少、子は増加ですから、図23の③に示したように、再生産関係を表すグラフ上の一点は次の年には左上の方向に移動し、それが3年続きます。また、④の期間では親は減少、子も減少ですから、再生産関係を表すグラフ上の一点は、次の年には左下の方向に移動し、それが1年続きます。
従って、1周期8年が経過すると図22の下段右端に図示したように、期間①では3年間にわたり点は右下に移動し、期間②では1年間だけ右上に、期間③では3年間にわたり左上に移動し、期間④では1年間だけ左下に移動します。
結果として、再生産関係は、反時計回りのループを描き、その傾きは負になります。
13.3 再生産関係のパターンは環境変動の周期と成熟年齢の比によって決まる
成熟年齢(m)が5歳以外の他のケースについてもすべて同様の説明が可能で、その結果を図24に示しました。m=0 の場合は、m=1 の場合と同じで、時計回りで傾きは正(m=0 の場合は傾きは1)になります。m=4 の場合は、m=5 の場合と同じで、反時計回りで傾きは負(m=4 の場合は傾きは-1)になります。従って、図24では、m=0の場合とm=4の場合は省略して、結果的に出現する6つのパターンを図示しています。

周期が他の長さを持つ場合も同じです。すなわち、成熟年齢mの大きさと環境変動の周期の長さ T との比(m/T)によって、6つのパターンのうちのどのパターンが出現するかが決まるということです。
13.4 再生産関係の傾きと成熟年齢の関係
図25は、日本沿岸および海外の計32系群について再生産関係の傾きと成熟年齢の関係を示したものです。黒丸は日本沿岸の系群のデータ、白抜きの四角は海外の系群のデータを示します。
成熟年齢が小さい時は再生産関係の軌道は時計回りとなり、成熟年齢が増大するにしたがって再生産関係の傾きは正からゼロ(無相関)、ゼロ(無相関)から負へと変化します。さらに、成熟年齢が大きくなると、今度は、再生産関係の軌道は反時計回りとなり、成熟年齢の増大に伴って再生産関係の傾きは負からゼロ(無相関)へと変化します。
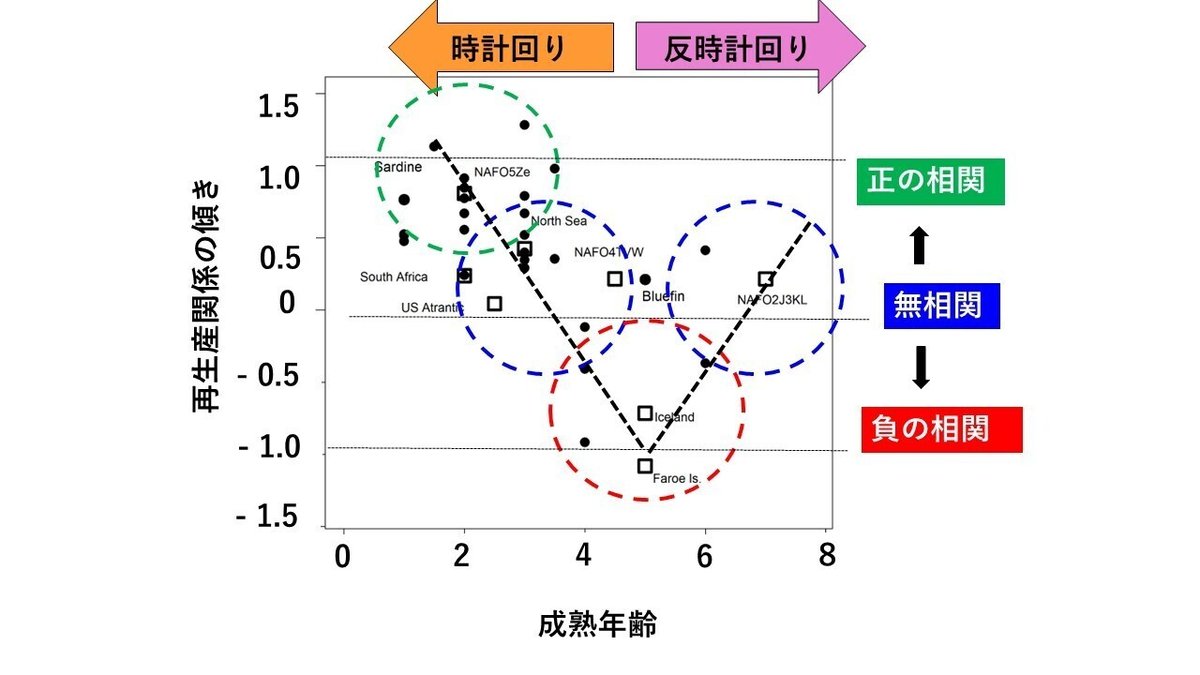
ただし、環境変動の周期は、海域によっても年代によっても異なるので、それぞれの系群ごとに環境変動の周期についても考慮する必要があります。しかし、そのような研究は、現時点ではほとんどなされていませんので、図25は系群ごとに考慮すべきである環境変動の周期の長さについては、とりあえず無視して描いた図ということになりますので、その点はご注意いただきたいと思います。
表1は、ある海域の海洋環境の変動の周期(T)を8年と仮定した場合に、その海域に生息するいろいろな成熟年齢を持つ魚の再生産関係のパターンがどのようになるかを示したものです。また、表1の右の欄には、それぞれのパターンに該当すると考えられる実際の系群を示しました。
ただし、実際の系群については、生息する海域がそれぞれ異なり、海洋環境の周期もそれぞれ異なります。また、系群によって成熟年齢も異なりますので、再生産関係の傾きと、時計回りか反時計回りかをもとに大雑把に分類を試みたものにすぎませんので、その点はご注意いただきたいと思います。
表1 再生産関係の傾きと成熟年齢の関係

大西洋クロマグロの場合は、西系群と東系群で、再生産関係のパターンが大きく異なりました。西系群の寿命は40歳程度と考えられており、寿命が極めて長いと言えます。
成熟年齢については、西系群の分布域である「メキシコ湾の漁獲物から計算した成熟率は11歳で56%と推定された」という記述があることから、平均成熟年齢もかなり高いことが予想されます。それに対して、大西洋クロマグロ東系群の寿命は40歳程度と西系群と同じく長命ですが、「すべての雌が産卵を開始する年齢は5歳と考えられており、これは大西洋クロマグロ西系群よりかなり若い」と記述されていることから、平均成熟年齢は両者でかなり異なることが予想されます。
今、環境変動の周期 T を20年程度と仮定すると、平均成熟年齢mが6歳から8歳ぐらいであれば、m/Tが0.3から0.4に相当するので、再生産関係は時計回りで傾きは負となります。従って、大西洋クロマグロ東系群はパターン3に該当すると考えられます。
大西洋クロマグロ西系群の場合は、環境変動の周期Tを同じく20年程度と仮定しますと、平均成熟年齢mが環境変動の周期と同程度か少し大きい20歳から23歳ぐらいであれば、m/Tが0.0から0.15に相当するので、再生産関係は、時計回りで傾きは正となります。従って、西系群の場合は、下段の方のパターン1に該当するのではないかと考えられます。
表1で、無相関で反時計回りとなるのは m/T が0.75前後ですから、太平洋クロマグロの場合は、環境変動の周期 T を20年程度と仮定すると、平均成熟年齢は15歳程度、環境変動の周期 T を15年程度と仮定すると、平均成熟年齢は11歳程度であれば、うまく表1の分類に合致します。最終的な結論を得るためには、環境変動の周期や平均成熟年齢の値等について、実データを用いた詳細な分析を行う必要があることは論を待ちませんが・・・。
スケトウダラの場合はともに、「寿命は不明であるが、10 歳以上、成熟年齢は4歳」とされており、両系群間で特別大きな差はないようです。しかし、漁獲物の年齢組成をみますと、スケトウダラ日本海北部系群は1-4歳が中心であるのに対し、スケトウダラの太平洋系群の方は4-6歳が多いということです。
漁獲物の年齢組成は、ある程度資源の年齢構成を反映しているものと考えると、スケトウダラの太平洋系群の平均成熟年齢の方が高いことが予想されます。今、環境変動の周期を20年程度と仮定すると、スケトウダラ日本海北部系群は時計回りで傾きが正ですから、平均成熟年齢が4歳程度であれば、m/T = 0.2となり、表1のパターン1に該当すると考えられます。
スケトウダラ太平洋系群の場合は、時計回りで傾きが負であるから、平均成熟年齢が6歳程度であれば、m/T = 0.3となり、表1に示したパターン3に該当すると考えられます。
14. 新しい資源変動の考え方に基づく再生産成功率の再現
既に述べたように、現行の資源変動理論と新しい資源変動の考え方の相違は、資源変動の主要因として、密度効果を重視するか否かの違いということになります。
現行の資源変動理論は「再生産成功率は密度効果によって、すなわち、親魚量レベルによって決定される」と考えるのに対して、新しい資源変動の考え方では、「再生産成功率は密度効果ではなく、環境変動によって決定される」と考える点が大きく異なっています(図26)。

従って、もし、新しい資源変動の考え方が正しいとすると、「再生産成功率は密度には関係なく、環境変動のみによって再現できる」ということになります。本節では、再生産成功率を環境変動のみによって再現した結果を紹介します。
14.1 使用する環境データ
ここで環境変動の指標として用いたものは、北極振動指数と、太平洋10年規模振動指数です。北極振動 とは、北極と北半球中緯度地域の気圧が相反して変動する現象のことです。北極振動指数が正の値を持つ時は北極付近が平年に比べ寒冷で、その周りの中緯度地域が暖かいという傾向があります。日本は中緯度地域にあるので暖冬になります。
反対に、北極振動指数が負の値を持つ時は北極付近が平年に比べ暖かく、その周りの中緯度地域が寒冷という傾向があります。日本は中緯度地域にあるので寒冬になります。このように北極振動指数は北半球全域の気候変動に影響を及ぼす環境指標と考えられます。北極振動指数のデータは1950年から年別、月別の値をインターネット上からダウンロードすることができます。
太平洋10年規模振動 とは太平洋各地で海水温や気圧の平均的状態が、10年を単位とした2単位(約20年)周期で変動する現象です。太平洋十年規模振動指数が正の値を持つ時は太平洋海域が平年に比べ冷たく、南半球が暖かいという傾向があります。日本は太平洋海域にあるので寒冷になります。太平洋10年規模振動指数のデータ は気象庁のホームページから1900年以降の年別・月別の値をダウンロードすることが可能です。
14.2 再生産成功率の再現結果
以下に示す12系群の再生産成功率は、平成2年度資源評価結果 のデータを用いて計算しています。
図27左上はマサバ太平洋系群の再生産成功率を再現したものです。青の細い線が実際に0歳魚尾数を親魚量で割って計算した値(引用した値)、赤の太い線が環境要因のみを用いて再生産成功率を再現した値です(参考文献5)。1992年の再生産成功率は親魚1キログラム当り29.5尾と高かったのですが、その年の値はうまく再現できています。

しかし、同じく再生産成功率が高かった1996年(75.4尾)、2004年(30.2尾)、2013年(52.2尾)、2018年(23.6尾)の値はうまく再現ができていません。このように個別に見れば、再現がうまくいかなかった年も少なからずありますが、全体的な増減のパターンはかなりよく再現できていると言えるのではないでしょうか。
マサバ太平洋系群のある年t年の再生産成功率を再現するときに用いた環境データは、2年前(t-2年)の2月、3年前(t-3年)の1月の北極振動指数と、1年前(t-1年)の8月、2年前(t-2年)の9月の太平洋10年規模振動指数の計4個の環境要因のみです。たった4つの環境要因で、これだけ長期間にわたる再生産成功率の変動のパターンが再現できてしまうというのは、むしろ驚くべき結果と言ってもいいのではないでしょうか?
図27右上はマサバ対馬暖流系群の再生産成功率を再現したものです。マサバ太平洋系群同様、うまく再現できていない年もありますが、全体的な変動傾向は、よく再現できていると言えます。
図27左下はゴマサバ太平洋系群の再現結果、図27右下はゴマサバ東シナ海系群の再現結果を示します。両系群とも全体的な変動傾向は、よく再現できていると言えます。

図28左上はスケトウダラ太平洋系群の再生産成功率の再現結果です。うまく再現できていない年もありますが、全体的な変動傾向は、よく再現できていると言えます。
図28右上はスケトウダラ日本海北部系群の再生産成功率を再現したものです。全体的に再生産成功率の観測値の方が、大きく変動しており、当てはまりはあまりよくありません。他の環境要因も加えて、さらに検討する必要がありそうです。
図28左下はマイワシ太平洋系群の再生産成功率を再現したものです。1988年、1989年、1990年、1991年の4年間は、特に大きな再生産成功率の落ち込みがあり、これが原因でマイワシは超低水準期に突入していくわけですが、これら4年間の落ち込みもうまく再現されていて、全体的な変動のパターンもよく再現されていると言えます。
図28右下は、カタクチイワシ太平洋系群の再生産成功率を再現したものです。1980年代前半、2005年と2019年は大きく外れていますが、それ以外の変動傾向はよく再現されています。

図29左上はスルメイカ秋季発生系群を、右上はスルメイカ冬季発生系群の再生産成功率を再現したものです。両系群ともが、全体的な変動のパターンはよく再現されていると言えます。
図29左下はホッケ太平洋系群の再生産成功率を再現したものです。2007年、2008年、2012年の高い再生産成功率の再現はうまくできていませんが、それ以外の全体的な変動のパターンは、よく再現できていると言えます。
図29右下はキンメダイ太平洋系群の再生産成功率の再現結果を示したものです(参考文献6)。キンメダイ太平洋系群の再生産成功率は、2018年は親魚量1キログラム当たり0.21尾と前年の値 0.35の40%減、2019年は0.05と前年の値の76%減と大きく落ち込んでいます。
1999年から2019年の平均の再生産成功率は0.36ですから、2019年の値は極めて低がったことがわかります。その原因がしばしば問題になりますが、このような急激な減少に環境変動が大きく関係していたことがかわかります。
上記の結果を見ると、キンメダイのように、水深200-250mの海底近くに生息する魚から、マイワシ、マサバ、スルメイカのように表層付近で生息する魚まで、また、北海道周辺のような寒冷な海域に分布するホッケなどの魚から東シナ海に分布するゴマサバ東シナ海系群のような魚に至るまで、北極振動指数や太平洋10年規模振動指数によって、再生産成功率の再現がある程度可能であるということは、驚くべきことではないでしょうか?
北極振動指数や太平洋10年規模振動指数といった巨視的な環境データではなく、対象生物が生息する海域の環境状態を、よりよく反映していると考えられる詳細な環境データが、もし利用可能であれば、もっと完璧に近いぐらいにうまく、再生産成功率の再現が可能になるであろうことは、十分に想像できると思います。
すなわち、このことは第6章で述べた「再生産成功率は環境によって決定される」という考え方が妥当なものであることを示しており、そのような考え方をベースとした新しい資源変動の考え方に基づく資源管理の方法について検討すべきであることを示しています。同時にまた、このことは密度効果を重視したMSY理論に基づく資源管理では、資源の管理はうまくいかないことを示しているということでもあります。
15 MSY理論が誤りであることを示すその他の例
最後に、MSY理論があやまりであることを示す2つの例を紹介して、本論を終えることにします。1つは水産庁が新しい水産資源の管理に導入した神戸プロット(後述)と言われる資源診断法ですが、皮肉にも、「神戸プロットはMSY理論が誤りであることを明らかにしている」ということを紹介します。2つ目は、同じく、新しい水産資源の管理で水産庁が公表しているゴマサバ太平洋系群の実施例を紹介し、MSY理論では、過去の資源変動が説明できないことを示します。
15.1 神戸プロットはMSY理論が誤りであることを示している
「新たな水産資源の管理」では、神戸プロット(または、神戸チャート)と呼ばれる資源診断手法が用いられています。
世界には5つの かつお・まぐろ類地域漁業管理機関 があり、地球上のほぼ全海洋をカバーしています。その5つの地域漁業管理機が、2007年に神戸で合同会議を開催しました。そのときに提案された資源診断法であることから、神戸プロットと呼ばれるようになり、その後、他魚種の資源管理でも広く使われるようになった手法です。
図30はマサバ太平洋系群に対して描かれた神戸プロットを示します。横軸に推定された現在の親魚量水準とMSY資源水準の比(現在の親魚量水準/MSY資源水準)をとり、縦軸には、推定された現在の漁獲係数 FとFMSYの比(現在の漁獲係数 F / FMSY )をとって、描いた図が神戸プロットです。
既に説明しましたが、MSY資源水準というのは、平均的にその水準に資源を維持しておけば、MSYが達成できる資源水準のことです。

また、漁獲係数Fとは、漁獲の強さを表す係数で、MSYの達成が可能な漁獲係数 F の値をFMSYと呼んでいます。例えば、FMSYの値が0.4である場合、現在の漁獲係数が F =0.8であれば、現在の漁獲係数 F はFMSYの2.0倍、なわち、現在の漁獲の強さは、MSYの達成が可能な漁獲の強さに比べて極めて高いということになります。
従って、もし、現在の親魚量水準/MSY資源水準(横軸の値)が1より小さく、現在の漁獲係数 F/ FMSY(縦軸の値)が1より大きい場合は、資源水準はMSY資源水準より低いにも関わらず、漁獲強度はMSYの達成が可能な漁獲係数 FMSYよりも強いということになり、明らかな乱獲状態にあると判断されます。
その反対の場合は、資源水準はMSY資源水準より高く、かつ、漁獲強度は目標とする漁獲強度よりも小さいので、乱獲の心配はなく、安全な状態(開発にまだ余裕がある状態)であると判断されます。もし、現状が乱獲状態にあると判断された場合には、F の値を小さくして(漁獲強度を下げて)、資源の回復を図るための管理措置をとらなければ、資源はさらに低下することになります。
しかし、皮肉にもこの神戸プロットは、MSY理論が誤りであることを明らかにしています。なぜなら、実際に観測される資源変動は上記で述べたような軌跡を示さないからです。
図30の2011年から2018年までの軌跡を見ると、いずれの年も親魚量の比は1 以下の領域にあり、漁獲係数の比は 1 以上の領域にあることがわかります(図の赤で示された領域にあります)。すなわち、乱獲状態にあることを示しています。しかも、2011年の横軸の値が約0.1ですから、2011年の資源量はMSY資源水準のわずか10分の1程度の極めて低い資源水準にあったことがわかります。
マサバ太平洋系群のMSY資源水準は154.5万トンと推定されていますから、2011年の親魚量がその10%程度ということは、約15万トン程度であったことになります。マサバ太平洋系群の禁漁水準は6.7万トンですから、2011年の親魚量、約15万トンというのは、禁漁水準にかなり近かったことになります。その時の漁獲係数 F とFMSYの比は、約1.7ですから、MSYが達成できる F の値の 2 倍近く(1.7倍)も強かったことになります。
極めて低い水準の資源に対して、極めて高い漁獲強度で漁獲を行っていた訳ですから、ひどい乱獲状態にあり、当然資源はさらに減少してしまうはずです。ところが、親魚量の比は2011年の0.1から2018年の 0.8 へとなんと8 倍にも増加しています。
MSY理論が正しければ、このようなことは、絶対に起こらないはずです。
すなわち、誰が見ても、図30の神戸プロットは、「MSY理論が誤りであることを証明している図である」ということになります。このような図を何のためらいもなく平気で公表している水産庁や水産教育研究機構の担当者の見識を疑わざるを得ません。
15.2 MSY理論では過去の資源変動の説明ができない
水産庁は「新しい水産資源の管理」をホームページ上で公開しています。図31はゴマサバ太平洋系群に「新しい水産資源の管理」をあてはめた場合のシミュレーション結果を示したものです。
上段の図が親魚量の経年変動を、下段の図が漁獲量の経年変動を示しています。また、2018年までが過去の実データの値を、2019年以降が「新しい水産資源の管理」を適用した場合のシミュレーション結果になります。
下段の図の横軸に平行の黒の実線は、1995年から2005年までの11年間の(図中①で示した期間の)平均漁獲量を示し、その値は13万トンになります。その下の赤い破線で示した値は、ゴマサバ太平洋系群のMSY、10.5万トンを示しています。すなわち、MSYの約24%(25,000/105,000=0.238)も高い漁獲を①の期間、すなわち、11年間も続けていたことになります。
持続的に漁獲できる最大の漁獲量(MSY)の24%も高い漁獲を11年間も続けていたわけですから、当然、親魚量は減少していくはずです。ところが、②の期間(2006年から2014年)、親魚量は急増し、漁獲量も急増しています。MSY理論が正しければ、このような現象は決して起こらないはずです。
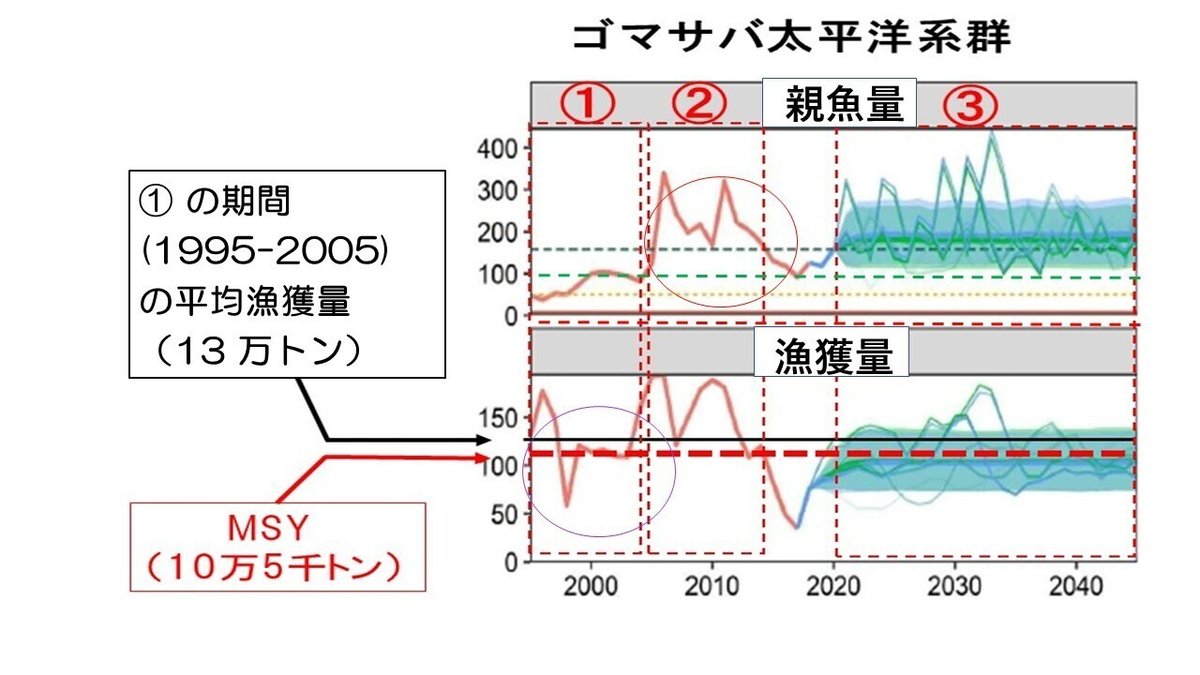
これについては、水産教育研究機構に公開質問状を提出し、上記の質問をしたところ、「②の期間で漁獲圧が過剰になっているにも関わらず、親魚量が増大したのは、2004年と2009年に卓越年級群が発生したためである」という驚くべき回答が返ってきました。
同じ年に生まれた魚の集団を年級群といい、ある年に生まれた0歳魚尾数が非常に大きい場合を卓越年級群と呼んでいます。卓越年級群というのは、魚の資源変動を調べていると、ごく普通に見られる現象です。
しかし、上記の回答は「②の期間での親魚量の急増は、MSY理論では説明できず、卓越年級群の発生という、全く別の要因を持ち出してきて説明しているわけです。すなわち、「MSY理論では、このようにごく普通にみられる資源変動の現象も説明できない」ということを認めていることと同じです。要するに、MSY理論は資源変動を説明するメカニズムとして妥当なものではないということです。
16. まとめ
密度効果を前提とした再生産関係は、それを支持する実際のデータがほとんどなく、架空のものである。
MSY理論は上記で述べたように架空の再生産モデルから導き出されたものであり、MSY理論も架空のものである。
MSY理論とは、持続的な漁獲量を最大にする最適な資源水準が存在するという考え方であるが、MSY理論そのものが架空のものであり、そのような最適な資源水準は存在しない。
MSY理論に基づく資源管理では、上記の最適な資源水準に資源を維持・管理することが目的ということになっているが、そのような最適な資源水準は存在せず、実在しない管理目標の達成を目的とした資源管理は意味がない。
再生産成功率は密度効果は、環境変動のみを用いて再現することが可能である。このことから、資源変動は、環境変動と漁獲により決定されることがわかる。
マサバの神戸プロットはMSY理論が誤りであることを示している。
ゴマサバに対して新しい水産資源の管理を適用した例は、MSY理論では資源の変動が説明できないことを示している。
誤ったMSY理論に基づいた資源管理の実施を中止し、環境変動を考慮したより柔軟で現実的な資源管理を実施すべきである(具体的な実施例は、参考文献 9 をご参照ください)。
参考文献
Sakuramoto K. 2014. A common concept of population dynamics applicable to both Thrips imaginis(Thysanoptera)and the Pacific stock of the Japanese sardine(Sardinops melanostictus). Fish Aqua Sci. 140-151. DOI10.4172/2150-3508.1000085.
Sakuramoto, K. and Suzuki, N. (2012) Effects of process and/or observation errors on the stock-recruitment curve and the validity of the proportional model as a stock-recruitment relationship. Fisheries Science, 78, 41-54. http://dx.doi.org/10.1007/s12562-011-0438-4
Tanaka, K., Suzuki, N. and Sakuramoto, K. (2017) Clockwise Loops and Anticlockwise Loops Observed in a Stock-Recruitment Relationship. Open Access Library Journal, 4, e3688. https://doi.org/10.4236/oalib.1103688
櫻本和美. (2018)マグロ類の資源管理問題の解決に向けて ―MSY理論に代わるべき新しい資源変動理論―. 水産振興605. http://www.suisan-shinkou.or.jp/
Sakuramoto, K. (2022). Erratum to “Reproductive Success in Fish Stocks Can Be Reproduced by Environmental Factors Alone” [Open Access Library Journal, 2021, Volume 8: e7636]. Open Access Library Journal, 9, e8231. doi: http://dx.doi.org/10.4236/oalib.1108231.
Sakuramoto, K. (2021). A Model that Forecasts Future Values of Reproductive Success for the Pacific Stock of Splendid Alfonsino. Open Access Library Journal, Vol.8 No.12, DOI: 10.4236/oalib.1108213.
Sakuramoto, K. (2015) A Stock-Recruitment Relationship Applicable to Pacific Bluefin Tuna and the Pacific Stock of Japanese Sardine. American Journal of Climate Change, 4, 446-460. http://dx.doi.org/10.4236/ajcc.2015.4503
櫻本和美. (2016)新しい水産資源の管理に向けて. 資源保護協会 季報548 (fish-jfrca.jp)
櫻本和美. (2021)ここが問題!新しい水産資源の管理 - MSY理論に代わる新しい資源変動理論 -. ∞ブックス. 276pp.
