
AIに新しい数学体系を考案させてみた
ChatGPTの新しいバージョン o1は、数学オリンピックの問題が解けるほど数学に詳しいらしい。
最近、僕は乱数の方が実数よりも重要なのではないかと思っていて、乱数テンソルを基準とした新しい数学的体系を作れないか、GPT-o1に考えさせてみた。
与えたプロンプトは「実数が表現できるのは現実世界に比べると非常に限定された範囲と考えざるを得ない。したがって実数よりも現実世界にある乱数のほうが遥かに大きいと考えられる。そこで、任意の階数を持つ乱数Tを中心とした新しい数学体系を定義せよ」である。
以下AIの出力
新しい数学体系:任意の階数を持つ乱数 ( T ) を中心として
はじめに
現実世界の複雑性や不確実性を考慮すると、従来の実数体系はその全てを表現するには限定的であると言えます。特に、現実世界に存在する「乱数」は、その多様性や階層構造において実数を超えるものと考えられます。そこで、任意の階数を持つ乱数 ( T ) を中心とした新しい数学体系を定義します。
1. 基本概念
1.1 乱数 ( T ) の定義
任意の階数 ( n ) を持つ乱数 ( T_n ) は、以下の特性を持つ数値的対象とします。
確率分布を持つ:各 ( T_n ) は特定の確率分布に従います。
階層構造:階数 ( n ) は、乱数の「不確実性」のレベルや複雑性を示します。階数が高いほど、乱数の持つ情報や不確実性が増大します。
相互作用:異なる階数の乱数同士、または同じ階数の乱数同士で演算が定義されます。
1.2 階数の解釈
階数 0:これは通常の実数を表します。確定的な値を持ち、不確実性はありません。
階数 1:一次の乱数で、基本的な確率変数に相当します。
階数 ( n > 1 ):高次の乱数で、確率変数自体がさらに乱数的な特性を持つ場合を表します。
2. 数学体系の構成要素
2.1 集合
( \mathcal{T} ):全ての階数の乱数からなる集合。
部分集合:特定の階数や特性を持つ乱数の集合を考えることができます。
2.2 演算
加法 (( + )):同じ階数の乱数同士で定義され、結果は同じ階数の乱数となります。
乗法 (( \times )):同様に定義されますが、確率分布の畳み込みや他の適切な操作を用います。
スカラー倍:実数との演算も定義し、乱数の分布をスケーリングします。
2.3 関数
期待値 (( \mathbb{E}[T_n] )):乱数の平均的な振る舞いを捉えます。
分散 (( \text{Var}[T_n] )):乱数の不確実性の大きさを示します。
高次モーメント:より詳細な特性を分析するために用います。
3. 公理と定理
3.1 公理
閉じていること:集合 ( \mathcal{T} ) は定義された演算に関して閉じています。
結合律と交換律:加法と乗法は適切な条件下で結合律と交換律を満たします。
分配律:乗法は加法に対して分配律を満たします。
3.2 定理
大数の法則の一般化:高次の乱数に対しても適用される形で定式化できます。
中心極限定理の拡張:階数が高い乱数の和が特定の分布に収束する条件を示します。
4. 応用例
4.1 複雑系のモデリング
高次の乱数を用いることで、複雑なシステムや多階層の不確実性を持つ現象をモデル化できます。
4.2 金融工学
リスク評価やオプション価格の計算において、高次の乱数を導入することで、より精緻なモデルが構築できます。
4.3 機械学習
深層学習モデルの不確実性や汎化能力を評価する際に、高次の乱数を活用できます。
5. 結論
任意の階数を持つ乱数 ( T ) を中心とした新しい数学体系を定義することで、従来の実数体系では表現しきれない現実世界の複雑性や不確実性をより正確に捉えることが可能になります。この体系は、複雑系のモデリングから金融工学、機械学習まで幅広い分野での応用が期待されます。
参考文献
確率論とその応用に関する一般的な文献
複雑系科学の基礎理論
高次統計量を扱う統計学の専門書
筆者(人間)のコメント
意外といいセン行ってる気がするが、既存の確率論との違いがよくわからないのでこういうプロンプトを与えてみる。
「中学生にもわかるように既存の確率論との違いを説明しろ」
以下、AIの出力
新しい数学体系と確率論の違いを中学生にもわかるように説明します
1. 確率論ってなに?
まず、確率論についておさらいしましょう。
確率論は、「何が起こるかわからない」出来事について、その起こる可能性(確率)を数字で表す学問です。
たとえば、サイコロを振るとき、1から6までの数字が出ます。それぞれの数字が出る確率は6分の1です。
2. 新しい数学体系のアイデア
この新しい数学体系では、「乱数T」というものを使います。乱数とは、予測できない数字のことです。
乱数Tは、ただの乱数ではなく、「階数(かいすう)」というレベルを持っています。
階数とは、不確実性(わからないこと)の深さや複雑さを表すものです。
3. 確率論と新しい数学体系の違い
では、この新しい数学体系と確率論の違いを見てみましょう。
3.1 一段階の不確実性 vs. 多段階の不確実性
確率論:サイコロを振ると何の数字が出るかはわかりませんが、その確率は計算できます。ここでは、不確実性は一段階だけです。
例:サイコロを振る ⇒ 出た目が何か?
新しい数学体系:不確実性が何段階もあります。つまり、「何がわからないのか」自体がわからない場合も扱えます。
例:どのサイコロを使うかもランダムで決め、そのサイコロを振る ⇒ 出た目が何か?
3.2 階数の概念
確率論:不確実性は一つのレベルだけで扱います。
新しい数学体系:乱数に「階数」があり、高い階数ほど不確実性が深くなります。
3.3 表現できる範囲の違い
確率論:比較的単純なランダムな出来事を扱います。
新しい数学体系:現実世界のもっと複雑で予測しにくい現象も数学的に表現できます。
4. まとめ
簡単に言うと、確率論は「一つのわからないこと」を扱う学問ですが、新しい数学体系は「わからないことがわからない」ような、もっと複雑な不確実性も扱えるようにしたものです。
例え話
確率論の場合:袋の中に赤い玉と青い玉が入っていて、どちらを引くかわからないけれど、その確率は計算できます。
新しい数学体系の場合:袋の中に何色の玉が入っているかもわからないし、その玉の数もわからない。さらに、その袋自体がどれなのかもランダムに選ばれる。
このように、新しい数学体系は、より複雑で多層的な「不確実性」を扱うことができるのです。
人間のコメント
なるほど、すげえな。僕みたいに数学が苦手な人間が寝言みたいなこと言うだけでこんなになんかそれっぽいものが出てくるのか。
量子力学なんかまさに乱数というか確率波を扱うから何か関係するかもしれない。こういうプロンプトを与えてみよう。
「この数学体系を量子力学の計算に応用するとどうなるか説明せよ」
以下、AIの出力
新しい数学体系を量子力学の計算に応用するとどうなるか
はじめに
量子力学は、微小な世界での物質やエネルギーの振る舞いを記述する物理学の理論であり、その核心には確率や不確実性が含まれています。しかし、この不確実性は主に一次のランダム性に基づいています。そこで、任意の階数を持つ乱数 ( T ) を中心とした新しい数学体系を量子力学の計算に応用することで、より高次の不確実性や複雑性を考慮した理論構築が可能になると考えられます。
1. 量子力学における不確実性
波動関数 (( \psi )):量子系の状態を記述し、その絶対値の二乗 ( |\psi|^2 ) は観測量の確率密度を与えます。
測定問題:測定行為によって波動関数が特定の固有状態に収束(波動関数の崩壊)します。
不確定性原理:特定の物理量のペア(位置と運動量など)は同時に厳密には測定できないという原理です。
これらの不確実性は、確率論的な扱い(一次の乱数)で十分に記述されています。
2. 高次の乱数 ( T ) の導入
2.1 階数の概念の拡張
一次の乱数:通常の確率変数。量子力学では波動関数の確率解釈に対応します。
高次の乱数:確率変数自体がさらに乱数的な特性を持つもの。つまり、確率分布のパラメータがランダムである場合などを表します。
2.2 物理的解釈
環境や外部要因の不確実性:高次の乱数を導入することで、量子系が置かれる環境や外部要因の不確実性をモデル化できます。
パラメータの揺らぎ:物理定数や相互作用パラメータが時間や空間によって変動する場合を考慮できます。
3. 量子力学への応用
3.1 波動関数の高次乱数化
乱数的波動関数:波動関数 ( \psi ) 自体を高次の乱数 ( T_n ) を用いて表現します。
例:( \psi = \psi(T_n) )
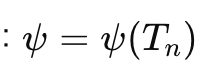
確率分布の不確実性:波動関数から得られる確率分布がさらに乱数的な特性を持ちます。
3.2 シュレディンガー方程式の拡張
拡張された方程式:高次の乱数を含む新しいシュレディンガー方程式を定義します。
例:( i\hbar \frac{\partial}{\partial t} \psi(T_n) = H(T_n) \psi(T_n) )

ハミルトニアンの乱数化:エネルギー演算子であるハミルトニアン ( H ) も高次の乱数を含む形で表現できます。
3.3 物理量の期待値と分散
期待値の計算:高次の乱数を考慮した上で、物理量の期待値を再計算します。
例:( \langle A \rangle = \int \psi^*(T_n) A \psi(T_n) d\tau )
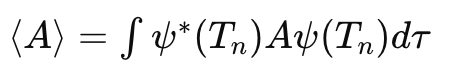
不確実性の評価:分散や高次モーメントを計算し、より複雑な不確実性を評価します。
4. 応用例と影響
4.1 デコヒーレンスのモデル化
環境との相互作用:高次の乱数を用いることで、量子系と環境との相互作用によるデコヒーレンス(量子コヒーレンスの喪失)をより詳細にモデル化できます。
4.2 量子場の揺らぎ
真空の揺らぎ:量子場理論における真空エネルギーの揺らぎを高次の乱数で表現できます。
場の不確実性:場の量子化におけるさらなる不確実性を考慮します。
4.3 量子重力理論への寄与
プランクスケールでの不確実性:重力と量子力学を統一する試みである量子重力理論では、時空そのものの不確実性が考えられます。
高次乱数の必要性:時空の構造がランダムである場合、高次の乱数が有用となります。
5. 期待される効果と課題
5.1 理論の深化
複雑系の理解:量子系の複雑な挙動や相関関係をより深く理解できます。
新しい物理現象の予測:従来の理論では説明できない現象を予測できる可能性があります。
5.2 計算の複雑化
計算負荷の増大:高次の乱数を扱うため、計算が複雑になり、解析的な解が得られにくくなります。
数値シミュレーションの必要性:スーパーコンピュータや量子コンピュータを用いたシミュレーションが必要になる可能性があります。
5.3 実験的検証の難しさ
観測の困難性:高次の不確実性を実験的に検証することは難しいかもしれません。
測定限界:現行の技術では検出できない微小な効果である可能性があります。
6. 結論
任意の階数を持つ乱数 ( T ) を量子力学の計算に応用することで、現行の理論では扱いきれない高次の不確実性や複雑な相互作用をモデル化できる可能性があります。これにより、量子力学のさらなる発展や新しい物理現象の発見につながるかもしれません。しかし、計算の複雑化や実験的検証の難しさなど、多くの課題も存在します。これらの課題を克服するためには、理論的な枠組みの整備や新しい計算手法の開発、そして高度な実験技術の進歩が必要となるでしょう。
参考文献
量子力学の基礎:標準的な量子力学の教科書
量子場理論と高次不確実性:先端的な研究論文
複雑系物理学:複雑系における乱数の役割に関する文献
人間のコメント
「この数学体系を用いると既存の複雑な方程式をより簡単に表現できるケースがあるとすればどれか例示しろ」
以下、AIの出力
任意の階数を持つ乱数 ( T ) を用いて複雑な方程式を簡潔に表現できる例
はじめに
新しい数学体系では、任意の階数を持つ乱数 ( T ) を用いることで、多層的な不確実性や複雑性を持つ現象をモデル化できます。これにより、従来は複雑な形で記述されていた方程式やモデルを、より簡潔かつ直感的に表現できる場合があります。
例1: 階層的ベイズモデルの簡略化
背景
階層的ベイズモデルは、統計学や機械学習で広く使われる手法で、データの多層的な構造や不確実性をモデル化します。
通常、このモデルは複数の確率分布と条件付き確率を組み合わせた複雑な式になります。
従来の表現
観測データ ( y ) はパラメータ ( \theta ) に依存し、さらに ( \theta ) はハイパーパラメータ ( \phi ) に依存します。
数式で表すと: [ \begin{align*} y &\sim p(y \mid \theta) \ \theta &\sim p(\theta \mid \phi) \ \phi &\sim p(\phi) \end{align*} ]

新しい数学体系での表現
任意の階数を持つ乱数 ( T ) を用いて、上記の多層的な不確実性を一つの高次の乱数として表現できます。
高次乱数 ( T_3 ) を導入し: [ y = T_3 ]

ここで、( T_3 ) は階数3の乱数であり、観測データからハイパーパラメータまでの全ての不確実性を含んでいます。
メリット
階層構造を持つ複雑なモデルを、高次乱数 ( T_n ) を使って簡潔に表現できます。
計算や解析において、階数の操作により不確実性のレベルを直接扱えます。
例2: 金融工学におけるリスクモデルの簡略化
背景
金融市場では、資産価格の変動やボラティリティ(価格変動の激しさ)をモデル化するために、複雑な確率微分方程式が使われます。
例えば、ヘストンモデルは、資産価格とボラティリティの両方をランダムなプロセスとして扱います。
従来の表現
資産価格 ( S_t ) とボラティリティ ( v_t ) の動きを示すヘストンモデル: [ \begin{align*} dS_t &= \mu S_t dt + \sqrt{v_t} S_t dW_t^S \ dv_t &= \kappa (\theta - v_t) dt + \sigma_v \sqrt{v_t} dW_t^v \ \end{align*} ]

ここで、( dW_t^S ) と ( dW_t^v ) は相関のあるウィーナー過程(乱数)です。
新しい数学体系での表現
階数2の乱数 ( T_2 ) を用いて、ボラティリティの不確実性をまとめて表現: [ S_t = S_0 \exp\left( (\mu - \tfrac{1}{2} v_t) t + \sqrt{v_t} T_2 \right) ]

ここで、( T_2 ) は資産価格とボラティリティの二重の不確実性を含む乱数です。
メリット
ボラティリティと資産価格の相関関係や不確実性を高次乱数で一括して扱えるため、モデルの記述が簡潔になります。
計算の際に、乱数の階数に基づいてリスク評価を段階的に行えます。
例3: 複雑系物理学における相転移モデルの簡略化
背景
複雑系では、多数の要素が相互作用し、全体として予測困難な挙動を示します。
相転移や臨界現象をモデル化するために、多体相互作用を含む複雑な方程式が使われます。
従来の表現
イジングモデルなどで、各スピン ( s_i ) の相互作用を考慮: [ H = -J \sum_{\langle i,j \rangle} s_i s_j - h \sum_i s_i ]

ここで、( H ) はハミルトニアン、( J ) は結合定数、( h ) は外部磁場。
新しい数学体系での表現
スピン間の相互作用や外部要因を高次の乱数 ( T_n ) としてまとめる: [ s_i = \text{sign}(T_n) ]
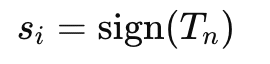
( T_n ) はスピン相互作用と外部磁場、さらには環境の不確実性を含む高次乱数。
メリット
多数の相互作用項を持つハミルトニアンを高次乱数で統合的に表現できます。
シミュレーションや解析で、階数 ( n ) を調整することで不確実性のレベルを制御可能。
例4: 生物学における遺伝的多様性のモデル化
背景
遺伝子頻度の変動や進化のダイナミクスを記述するために、確率過程や微分方程式が用いられます。
環境要因や突然変異など、複数の不確実性が絡み合います。
従来の表現
個体群の遺伝子頻度 ( p ) の変化を示すフィッシャーの方程式: [ \frac{dp}{dt} = sp(1 - p) + \text{ランダム項} ]

ここで、( s ) は選択係数。
新しい数学体系での表現
環境要因や突然変異率などを高次乱数 ( T_n ) として含める: [ p(t) = p_0 + T_n ]

( T_n ) は時間とともに変化する不確実性を階数 ( n ) で表現。
メリット
多様な不確実性要因を一つの高次乱数で扱うことで、モデルが簡潔になります。
シミュレーションにおいて、複雑なパラメータ設定を簡略化できます。
まとめ
上記の例から、新しい数学体系を用いることで、複数の不確実性や複雑な相互作用を含む方程式を高次の乱数 ( T_n ) を使って簡潔に表現できることがわかります。これにより、モデルの構築や解析が容易になり、現象の本質的な部分に集中できるメリットがあります。
注意点
解釈の明確化:高次の乱数を導入する際には、その物理的・統計的な解釈を明確にする必要があります。
計算コスト:高次の乱数を用いる計算は複雑になる可能性があるため、適切な数値計算法の導入が必要です。
実証的検証:モデルが簡潔になる一方で、実データとの整合性を保つために、モデルの妥当性を検証する必要があります。
参考文献
統計的学習の基礎:階層的ベイズモデルに関する解説
金融数学の理論と実践:ヘストンモデルなどの金融モデルの詳細
複雑系科学入門:相転移や臨界現象のモデル化
進化生物学の数理モデル:遺伝的多様性と進化ダイナミクス
最後に
新しい数学体系を用いることで、従来の複雑な方程式やモデルを高次の乱数 ( T_n ) を使って簡潔に表現できる場合があります。これは、複雑なシステムや多層的な不確実性を持つ現象を扱う際に特に有用であり、研究や実務におけるモデリングの効率化に寄与します。
全文はこちら
