
★結晶群の一般化(2)
◆古典結晶空間群
3次元の結晶空間群が230種あることの数え上げは,1890年ごろ,フェドロフ(ペテルスブルグ大,鉱物学),シェンフリース(フランクフルト大,数学),バーロー(ロンドンの事業家)により,それぞれ独立に達成された.これは,X線の発見以前の19世紀末の数学的業績で,X線の発見で幕を開ける20世紀に発展する結晶構造解析の基礎となった.
*1)⇒構造解析にどのように役立つか
フェドロフが数え上げた方法を理解し易くするために,まず,2次元の結晶空間で説明しよう.2次元の結晶空間群(平面群),つまり,壁紙模様の対称群は17種類ある.そもそも,結晶空間=周期的な空間,つまり,単位胞が隙間なく繰り返し並んでいる空間であり,「単位胞でデジタル化された空間」と言える.2次元結晶空間なら,1つのタイル(単位胞に相当)で,タイル張りされた平面である.
●2次元は表面だけの世界で,表面には裏表の区別はない.3次元にいる我々は,平面に裏表の2面があるように思うかもしれぬが,その場合は「層」と言い「表面」とは言わない.従って,壁紙模様は表面だけの平面であり,表面を裏返す操作は,2次元結晶群にはあり得ない.
●表面をタイル張りすれば,必ず周期が生じるわけではない.ペンローズ・タイリングがその例だが,非周期なタイル張りもいくつか存在する.
結晶空間の定義には周期性が必須で,ペンローズ・タイリングのような構造をもつ物質は「結晶」の範疇ではなく,「準結晶」と呼ばれる.
*2)⇒非周期タイリング
◆フェドロフの数え上げ方法
周期的な平面タイル張が可能なタイルの形は平行多辺形で,平行4辺形,および,平行6辺形がある.
対称性で,平行多辺形を分類すると:一般的な平行4辺形,ひし形,長方形,正方形;一般的な平行6辺形,つぶされた正6角形,正6角形:がある.
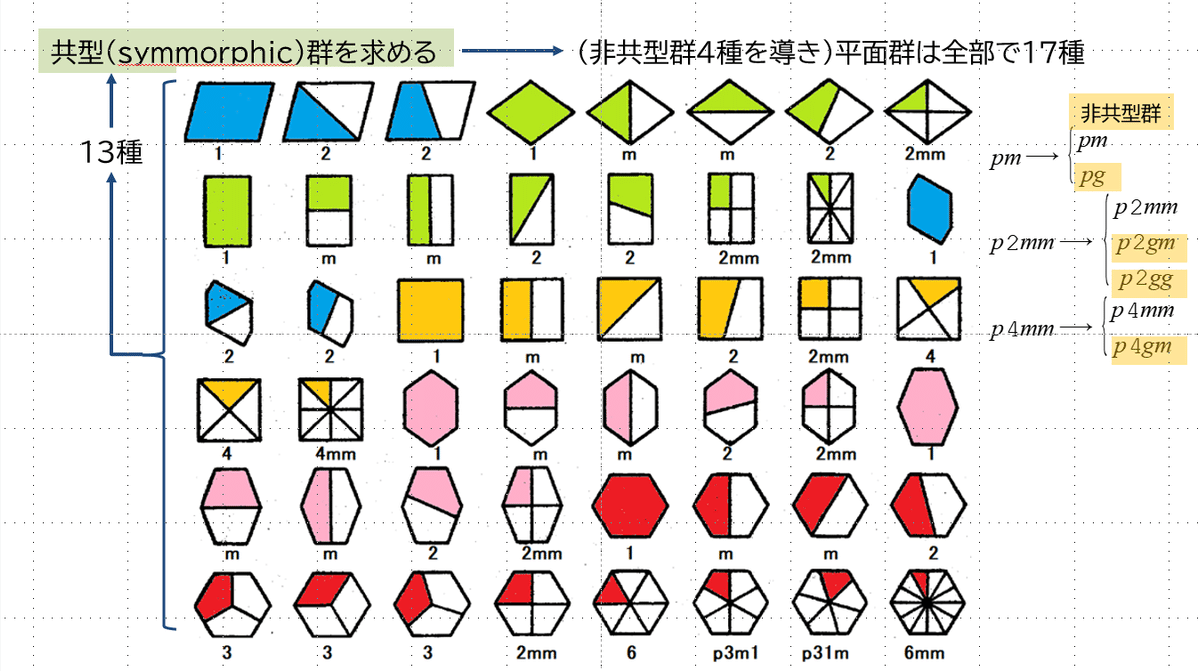
これら7種類の有限図形を,等価な部分に分割した図の一覧を以下に掲載した.これらの分割様式を対称性で分類すると,共型群13種が得られる.さらに,このうちの3種の共型群からは,非共型群4種が導けるので,計17種の2次元空間群(壁紙模様)が得られる.*3)⇒共型,非共型の解説
フェドロフらは,3次元空間群の導出で同様な方法を用いた.2次元では平行多辺形から出発したが,3次元ではフェドロフの平行多面体5種から出発する.

◆結晶空間群
並進群=独立な並進ベクトルの1次結合が生成する群
結晶空間(周期的な空間)は,単位胞でデジタル化さた空間なので,単位胞を格子点で代表すれば結晶格子が得られる.
点群=1点を特異点とする対称操作の組合せが作る群.
点群と結晶空間の周期性(結晶格子)とが両立しなければならないので,回転対称操作には制限が生じ,このような点群は結晶点群と呼ばれる:回転対称操作は,2回軸,3回軸,4回軸,6回軸に限られる.
●古典結晶群は,「幾何空間」内の対称変換のみで生成されるのだが,幾何空間に特性次元(例えば"色”)を付与した「超幾何(色付き幾何空間)」内の対称変換を考え,黒白群,色付き群,および,群の一般化へと発展する.*)⇒第2部
●互いに双対な図形の対称性は同一.従って,Fourier変換で結ばれる双対空間の対称性は同一である.結晶構造とそのX線散乱振幅はFourier変換で結ばれるから,対称性は同一である.しかし,結晶とそのX線回折強度像(散乱振幅の絶対値の2乗)の対称性は,同一ではなく,X線回折強度像の対称性は結晶の対称性よりも上昇し得る.これは,ピエール・キュリーの因果律の例でもある.*4)⇒X線の散乱
●鏡映操作と回転操作には本質的な違いがある:3次元空間の鏡映像(互いにキラル)は3次元空間内の運動で物体に重ねることができない(ただし,次元を1つ上げた4次元空間ならばこれは可能).3次元点群の対称操作は,3次の直交行列で表現できるが,その行列式が;回転操作では+1,鏡映操作や対称心であることに違いがある.
$${\left( \begin{array}{cc} \text{cos}\theta & \text{sin}\theta \\ \text{-sin}\theta & \text{cos}\theta \end{array} \right)}$$ 回転操作の例
$${\left( \begin{array}{cc} 1 & 0 \\0 & -1 \end{array} \right)}$$ 鏡映操作の例
◆今回必要となる群概念ミニマム
群,部分群,正規部分群,共役類,群の拡大,準同型,同型.
対称性の高低と部分群の列(正規列,非正規列).
●群の定義
$${G=\{a, b, c, \cdots \}}$$ 集合$${G}$$が群と呼ばれるのは,次の公理を満たす場合である:
0) $${\forall a, b\in G → a\cdot b\in G}$$ 任意の2元に2項演算$${\cdot}$$が定義される.
1) $${(a \cdot b)\cdot c=a \cdot (b \cdot c)}$$ 結合律
2) $${a\cdot e=e\cdot a=a}$$ $${e}$$: 単位元,左単位元
ある元$${e}$$(ただ一つ)が存在し,すべての$${\forall a\in G}$$に対して成立.
3) $${a\cdot x=x\cdot a=e}$$ $${x=a^{-1}}$$: $${a}$$の逆元,左逆元
$${ a\in G}$$に対して,$${x}$$が(ただ一つ)存在する.
1)~3)を群の公理という.
群の公理中の(ただ一つ)というのは,公理に含めなくてもよい(導くことができる).

●正規部分群の定義
群$${H}$$が群$${G}$$の正規部分群($${H⊲G}$$と表記)であるとは,
任意の$${a∈G}$$に対して$${aHa^{-1}=H}$$,(つまり,$${aH=Ha}$$)となることである.
群$${G}$$がAbel群ならば,すべての部分群は正規である.
2つの自明な正規部分群(自分自身と$${\{e\}}$$)以外に,正規部分群を持たない群を「単純群」という.(単純群の定義)
正規部分群に関する2つの左剰余類の積では,$${aH\cdot bH=a\cdot bH}$$が成立する.従って正規部分群を核として商群$${G/H}$$が作れる.
群$${G}$$の非正規な部分群$${H}$$に関してもラグランジュ展開(直和分解)は作れるが,剰余類の積を行うと,バラけてしまい結果は1つの剰余類に収まらない.
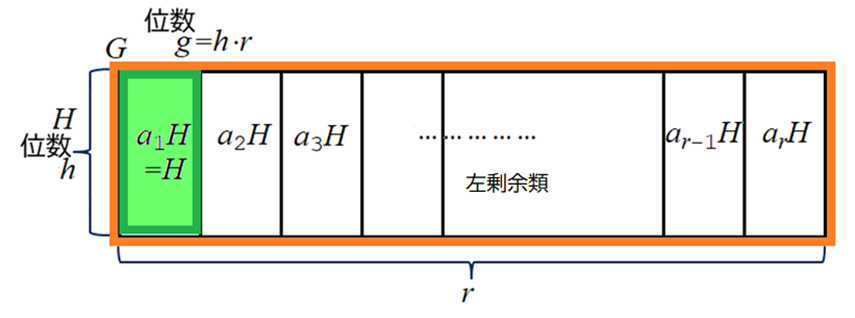
●ラグランジュ展開: $${G \vartriangleright H}$$のとき
$${G=a_{1}H \cup a_{2}H \cup \cdots \cup a_{r}H}$$, $${a_{1}=1}$$
$${G}$$は適当な$${a_{i} \in G}$$を$${r}$$個選び,$${r}$$個の剰余類の直和に展開される.$${r}$$は意に決まる.
$${r=g/h}$$ (ここで,$${g}$$: $${G}$$の位数,$${h}$$: $${H}$$の位数,$${r}$$: 部分群の指数)
[演習]
点群$${4mm}$$には,$${2mm}$$あるいは$${4}$$や$${2}$$が正規部分群として含まれる.点群$${4mm}$$の正規部分群を核として準同型写像すると,点群$${4mm}$$は商群に還元できる:$${4mm/2mm≅4}$$(mod2),$${4mm/4≅m}$$,$${4mm/2≅4mm}$$(mod2). 部分群$${m}$$は正規部分群ではないので,ラグランジュ展開はできるが,剰余類は群をなさない.このように,大きな群は,その正規部分群を,何らかの部分群(あるいは正規部分群)で拡大した構造になっている.
非正規の部分群を,何らかの非正規部分群で拡大した構造は,非正規の拡大という.非正規拡大は難問.例えば,部分群$${K}$$の共役集合の重畳という構造をもつ代数系(特殊な亜群)などがある.*)⇒今回は除外

●共役類
群Gの元$${g', g}$$は,$${g'=aga^{-1}}$$,($${ a\in G}$$)のとき,互いに共役$${g' \sim g}$$という.互いに共役という関係は同値関係である.
集合$${S\subset G}$$に対して,$${aSa^{-1}}$$, ($${a\in G}$$)となる集合は,集合$${S}$$と共役 な集合である.$${S}$$が部分群であれば,$${aSa^{-1}}$$は$${S}$$に共役な部分群である.物理的な効果が同等な対称操作は同じ共役類に属することがわかる.
例として,表中に点群$${4mm}$$の共役類を色分けで表示した.

◆群の行列表現には,今回は深入りしない
異値の既約表現の数は共役類の数だけある.例えば,シクロブタジエン(点群$${4mm}$$)のπ電子系の分子軌道(4つの C 原子の原子軌道の線形結合)の永年方程式(固有値問題)を解き,エネルギー準位などが求まる.あるいは,4つの原子軌道関数を基底にして作った分子軌道(点群$${4mm}$$)の正則表現を簡約して,それに含まれる既約表現を求めるのだが,各既約表現はエネルギー準位に対応する.*)⇒表現
◆結晶空間群の作り方
●格子を,対称性で分類したものがブラベー格子で,2次元ブラベー格子は5種類ある.2次元には,互いに独立な並進ベクトル2つがとれ,この2つの並進ベクトルの組を対称性で分類すると5種類になる.格子点間の垂直2等分線で囲まれる図形を「ディリクレ胞」というが,「ディリクレ胞」の形で分類したと思うとわかり易い.


空間群には,正規部分群として並進群(格子)が含まれているので,並進群を結晶点群で拡大して空間群が得られる.組み合わされる点群は格子と両立する対称性のものである.一例として,直方(長方形)単純格子の格子点に,点群$${2mm}$$の有限図形を配置して,空間群$${P2mm}$$が得られる.$${P2mm}$$は共型群である.点群$${2mm}$$の鏡映操作$${m}$$を,映進操作$${g}$$で置き換えることを考える.映進操作$${g}$$とは,鏡映と鏡映面に沿った周期$${T/2}$$の並進を組み合わせた操作のことである.したがって,映進を2回繰り返すと,$${g^2=T}$$となり,格子分だけの移動になる.結晶格子は無限に繰り返すので,並進周期だけ移動した点はすべて同値である.そこで,映進操作,$${g^2=1(\text{mod}T)}$$は,周期的空間の対称操作となる.共型群$${P2mm}$$から非共型群$${P2mg,P2gg}$$が導ける.映進操作$${g}$$は,非対称要素(モチーフ)を隣の胞に移動させてしまうが,格子並進群を法として同値とすれば,単位胞内に(還元)引き戻せる.

群$${G}$$はその部分群$${H}$$に関して剰余類の直和にラグランジュ展開できる. 空間群の拡大では,正規部分群は非常に重要な役割を演ずる.$${H}$$が$${G}$$の正規部分群であるとき,$${H}$$に関する剰余類は,$${H}$$を法として商群$${G/H}$$をなす.逆に,$${\{a_1, a_2, \cdots , a_r \}=G^*}$$とし,正規部分群$${H}$$を群$${G^*}$$で拡大して$${G}$$が得られるのだが,$${G^*}$$も正規部分群である場合は直積;$${G^*}$$が非正規の部分群である場合には半直積;$${G^*}$$が$${H}$$を法として群となる(モジュラー群)の場合には条件積;で表現する.
引用:
Symmetry in scienve and art; A.V.Shubnikov and V.A.Koptsik
美しい幾何学; 谷克彦
