
意味の構築:犬かダチョウか
以下のエッセイを要約しました.
By Rachel Thomas, Submitted by Rachel on July 28, 2020Rachel Thomas is Editor of Plus. She spoke to Yoshua Bengio at the Heidelberg Laureate Forum in September 2019.
世界のモデルを構築する上で重要なのは,意味を構築する方法です.子どもたちは,写真や実生活でほんの数例を見て,「犬」という言葉の意味をすぐに理解します.彼らは,直感的に,さらに高レベルの表現(生きている,動物,4本の足,毛皮で覆われた)を構築します.
さらに,彼らは簡単に概念を一般化します.片足が足りない犬は,足が3本しかないにもかかわらずやはり犬です.彼らは非常にすばやく動物が犬であるかどうかを知ることができます.子どもたちは,非常に小さなデータセットからこれらのもっと高レベルの理解を構築し,データセットの変化(さまざまな種類の犬やさまざまな種類の動物を見て)にすばやく適応できます.

これは犬ではありません.猫でもありません.thiscatdoesnotexit.comの機械学習アルゴリズムによって創造されたものです.
機械学習はごく最近になって,非常に進歩しました.これはディープラーニングの登場のおかげです.ヨシュア・ベンジオは,ディープラーニングを機械学習と人工知能の重要な部分にするのに役立つ画期的な功績により,2018年のチューリング賞を受賞しました.
機械学習とは,人間のプログラマーが明示的にその方法を教えるのではなくて,機械が特定タスクを行う方法自体を学習することを指します. 1980年代以降,ニューラルネットワークは機械学習の数学モデルとして使用されてきました.私たちの脳の構造に触発されたもので,各「ニューロン」は,数値を入力として受け取り,数値を出力する単純な数学計算であります.
これらのニューロンは層状に配置され,層内のニューロンは,前の層のニューロンの出力の加重和を入力として受け取ります.人間はネットワークの構造を決定しますが,これらの加重和の重みには関与しません.これらはネットワークを介して多数の例を実行する訓練プロセスを通じて学習され,特定タスクに最適な結果を得るように重みを微調整します.
元々,機械学習で使用されるニューラルネットワークは比較的単純でした.訓練プロセスの計算が複雑になるため,ニューロンの1つまたは2つの層のみで構成されていました.しかし,2000年代の初めに,ベンジオとその同僚たちは,彼らがディープラーニングと呼んでいるものに取り組み始めました.
分散表現
ディープラーニングは他の機械学習方法よりも優れています.それはマシンに良い表現を構築する能力を与えます.表現とは,マシンが概念を格納する方法です.古典的な人工知能(機械学習以前)では,人間が機械に必要な知識を教えていました.アルゴリズムは人間のプログラマーによって書かれた一連のルールのようなものであり,概念は象徴的に表現されました(たとえば,変数「cat」は,何かが猫でない場合は0に設定され,何かが猫である場合は1に設定される).1990年代にチェスのグランドマスターであるギャリーカスパロフ氏を倒したディープブルーは,IBMが開発したチェス用コンピューターで,この種の古典的な人工知能の例です.
ディープラーニングの重要なアイデアは,概念がベクトル(値の配列)----つまり,分散表現----として表現するということです. 例えば,「猫」という単語を,ベクトルで表すと,
[-0.241414、0.287426、0.165113、-0.431581、-0.087530、0.561078、-0.415193、0.003364、0.016638、0.030558、0.137265、-0.101964、-0.144205、0.200312、-0.440345、0.782978、0.215758、-0.397508、-0.132525、0.392892、 0.187668、0.190704、-0.597705、-0.473172、-0.046912、-0.655475、0.297324、-0.044785、0.907623、0.090989、0.330201、-0.218510、0.442974、-0.197005、-0.013970、-0.048274、0.016939、-0.304073、-0.458688、0.839282 、0.364900、-0.573024、0.130873、-0.267990、0.109434、0.146609、0.497982、-0.281677、0.415757、-1.341299、0.755230、0.274921、-0.261315、0.316203、-0.266019、0.077696、0.086259、-0.148955、0.111285、0.905508、-0.499343 、0.220561、-0.060084、-0.138308、0.263414、0.029885、-0.030825、-0.700774、-0.250947、-0.387521、0.167361、-0.278134、-0.658570、-0.117905、0.114435、0.236835、0.319998、-0.212485、-0.675103、0.043290、 -0.045866、0.771321、0.205061、-0.775832、0.429374、0.097047、0.065185、0.233347、-0.138985、-0.095526、-0.002476、0.221378、-0.443003、-1.068492、-0.282422、-0 .356644、-0.192903、-0.000860、-0.015085、0.294197、0.318298、-0.105752、0.045668、-0.191743、-0.108592、-0.211702、-0.278396、-0.444925、0.075270、-0.043502、0.372264、-0.520599、-0.189202、- 0.411445、0.320581、-0.242174、-0.208912、-0.571741、-0.146618、0.231338、0.077776、0.508152、-0.499199、-0.345736、0.026528、0.228578、-0.790778、-0.094263、0.304350、0.644286、0.559164、0.067319、-0.223100、- 0.267459、-0.116927、0.696897、-0.250773、-0.339711、0.295284、0.148529、0.139849、-0.526502、0.379415、-0.517519、0.025815、0.136009、-0.090450、0.061950、-0.496813、0.326041、0.528336、-0.664441、0.888717、-0.210583 、0.210085、-0.250152、-0.464110、-0.398434、-0.097318、-0.136705、0.734923、0.024840、0.186065、0.656894、0.442599、0.538127、0.598445、0.550830、0.608239、-0.210517、0.262453、-0.103285、-0.163599、-0.091919、 0.283204、-0.239344、0.328113、-0.064806、-0.206737、0.552150、0.391778、-0.137410、-0.270437、0.440234、-0.623495、-0.064421、0.352393、0.086501、-0.191278、-0.642643、- 0.126353、0.180774、-0.417938、-0.199682、-0.310765、0.267943、0.419079、-0.060403、0.264354、0.033174、0.114115、-1.067016、0.102984、0.220216、0.196559、-0.061410、0.074493、0.447212、-0.018113、-0.605357、-0.660194 、0.019961、0.547134、0.048423、-0.077267、0.035326、0.410081、-0.600771、0.138824、0.377122、-0.396284、0.173469、0.525796、0.276606、0.344208、0.553607、0.018219、-0.085965、0.190523、0.099517、0.636050、0.756199、-0.295487、 -0.309625、-0.140817、-0.497444、-0.403202、-0.304629、-0.128906、0.153457、0.845987、0.190644、0.217209、0.054643、-0.063143、-0.057904、0.143839、-0.300590、-0.399825、0.106663、0.235159、1.040565、-0.074484 、0.324786、-0.257785、0.673381、0.097968、-0.361923、-0.282786、0.173656、0.334292、0.083597、0.048122、-0.148704、0.443468、0.240980、0.264529、0.165889、-0.219577、0.309359、0.134012、-0.141680、0.023127、0.058023、 0.074283、-0.490581、0.288622、0.284951、0.066673、0.302247、0.081319、-0.383685、-0.052862、0.244946、-0.344482、-0.072416、0.8 04204、-0.042981、-0.226182、0.482332、-0.163026、-0.414333、-0.399022、-0.424497、-0.245093、-0.040660、0.263090、0.326652、-0.317213、0.222228] =猫
そして最も重要なことは,ベクトル表現は人間によって機械に与えられたものではなく,訓練データのセットを処理した後に機械自身が学習したものです.たとえば,GloVeの教師なし学習アルゴリズムは,wikipediaのすべての記事をデータセットとして訓練され,このデータセットのすべての単語のベクトルを学習します. (Jay Alammarによる優れた記事で詳細が読めます.ここの例は,wikipediaで訓練されたGLoVeのデータセットを使用します)
もっと深い意味
分散表現を学習することで,マシンは語彙の高レベルの意味にアクセスできます. 高次元空間での単語の位置として単語ベクトルを考えると,類似した単語は互いに接近しています. たとえば,この方法で訓練されたマシンの「カエル」に最も近い単語は,カエル,ヒキガエル,トカゲ,リトリア,レプトダクティルダエ,ラナおよびエリュートロダクティルスです(最後の4つはすべてカエルの特定の種です). それらが近接しているということは,それらの単語ベクトルのすべてのエントリに対して,すべてが非常に類似した値を持っていることを意味します. しかし,以下のJay Alammarによる図で示されているように,単語ベクトルの一部あるいは同様の値を使用するだけで,マシンはより高いレベルの意味にアクセスできます. Alammarは,色を使用して単語ベクトルの数値を表します.最高値の赤からゼロの白,最低値の青まで,数値を表します.
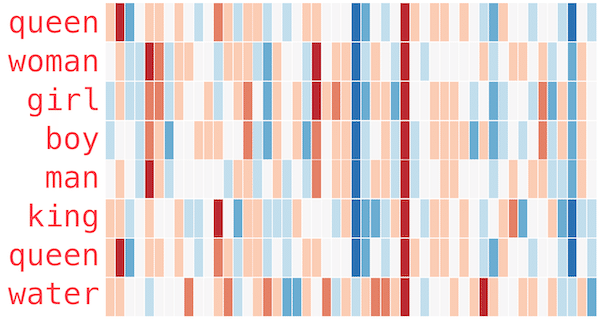
幾何学的に,特定の入力の類似した値は,これらのベクトルによって表される単語がすべて,ある意味で,特定方向に並んでいることを意味します.コンピューター科学者は,主成分分析と呼ばれる統計的手法を使用して,単語のベクトル空間でこれらの幾何学的特徴を識別します.これらの幾何学的特徴が概念的にどのように並ぶかを想像することもできます.人を示すすべての単語に同様の値が並んでおり,これらの中で,女性と少女,または少年と男性を示す単語の類似性が高くなっています.これらの単語の分散表現の幾何学的特徴により,機械は単語のより抽象的な,より高レベルの意味を学習することができます.
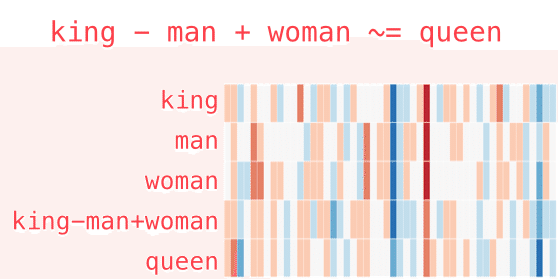
驚くべきことに,ベクトル空間におけるこれらの種類の単語の埋め込みは,特定の種類の単語の算術にも適しています.これは,ベクトル加算を使用して解決する例です: "king"-"man" + "woman".マシンにこれらの単語の意味が与えられたことがないにもかかわらず,分散表現により,マシンは単語の性別などのより高レベルの意味にアクセスできます.このデータセットの例では,この計算に対する答えに最も近い単語ベクトルは「クイーン」です.
同様に,機械学習アルゴリズムをテキストではなく画像のデータセットで訓練して,画像の分散表現を学習できます. (これがどのように行われるかは,対面で確認できます)この場合,画像はベクトルで表され,機械学習アルゴリズムの目的は,類似するものの画像のベクトル表現をクラスター化することです.
猫の画像のベクトル表現は一緒にクラスター化し,そのクラスターは,仲間の哺乳類,犬の画像のクラスターに何らかの方法で近く,カエルの画像のクラスターからさらに離れている可能性があります.また,画像ベクトルの同様の値は,画像内の特定の共有機能に対応します.これは,GLoVeのアルゴリズムが性別の単語について学習したのと同じように,画像内の性別のある特徴を区別するなど,画像認識に大きな進歩をもたらしました.しかし,マシンはまだ人間レベルのAIにはほど遠い.人間の目では決して気づかないのだが,画像のほんの数ピクセルをいじるだけで,意図的にマシンをだますことができます.
ーーーー以下略ーーーー
