これもピタゴラスの定理

直角3角形△ABCの面積（赤色）は，直角を挟む２辺上の三日月の面積（水色，黄緑色）の和です．証明してください．

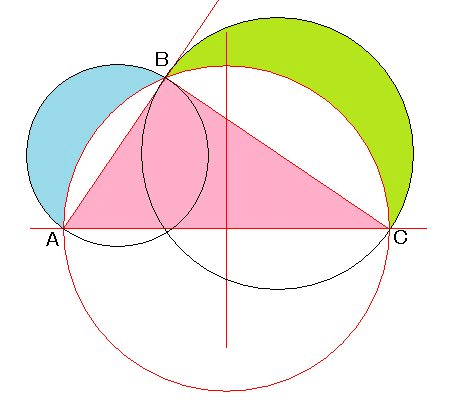
∠ABCは直角，３つの円はそれぞれ，各辺を直径とする円です．
ピタゴラスの定理 AB^2+BC^2＝CA^2 を持ち出してかまいませんが，
この問題は，ピタゴラスの定理と同じことを言っています．

(ヒント)
ピタゴラスの定理から，３つの半円の面積の間に，
青の3日月を含む半円+緑の三日月を含む半円=赤の三角形を含む白い半円
が成り立ちます．赤い三角形の外側の白い２つの月形部分は，
両辺に共通に含まれていますから，両辺から減じると証明できます．