平行、半平行、等面積

<<KVANTIK>>, No.11, 2020; Фёдор Ниловフョードル・ニーロフより抜粋

次の図を観察してください．

白い正方形を一斉にペチャンコにすると図形をコンパクトにすることができます．不思議ですね．

パラレルニクという多角形は，下図のどちらかの性質を持ちます．

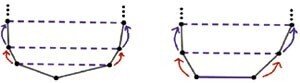
任意の平行多角形はパラレルニクである．下図に示す例は5角形の平行多角形の例です．

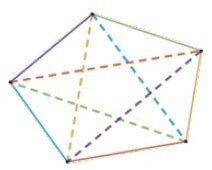
次の図は，中央に任意の３角形（緑）があります．その外に白い正方形を３つ作ります．それら頂点は，6角形になり，その外に白い正方形を３つ作ると，また6角形が得られます．同じ色の多角形の面積はすべて等しく，4角形はすべて台形です．この定理は，2001年にアメリカの数学者D. DeTemple と M. Hudelsonが証明しました．

また，中央の３角形をどんな平行多角形に置き換えてもこの定理が成り立つことも発見しました．以下の図は，中央に平行４角形，平行５角形にした例です．