
「かつ」「もし」「ならば」で「複合判断」へ〜中学生からの論理学入門 付録
本記事は投げ銭スタイルです! 応援よろしくお願いします。
「SはPである」という、単に「〜である」と断定する最も単純な判断のことを単純判断や定言判断とよぶ。
主語と述語が「かつ」「または」などの接続詞で結合されて複数になっている場合がある。
加えて、判断そのものが接続詞で結合されている場合もある。これらの接続詞で複数の判断が連結された判断を複合判断とよぶ。
重要な接続詞は3つ
論理において重要な接続詞は3つだ。
「かつ」「または」「(もし〜)ならば」である。
なぜ3つだけなのかと言うと、定言判断pとqの基本的な関係は以下の3パターンだけだからだ。
pとqが両方共に成り立つ。 : 「pかつq」
pとqのどちらか一方が成り立つ。 : 「pまたはq」
pが成り立つ場合、qが成り立つ。 : 「pならばq」
「かつ」を連言、「または」を選言、「もし」を仮言という。
連言(「かつ」)
「かつ」の意味
「pかつq」は「pとqが両方共に成り立つ」という意味である。
もう少し詳しく理解するために、「pかつq」をpとqに分解してみると以下のようになる。
1.pが真であり、同時にqも真であるとき
⇒ 「pかつq」が真である
2.「pかつq」が真であるとき
⇒ 「pが真」と「qが真」の2つの主張が導ける
連言の判断
連言「かつ」で述語Pが連結された判断は以下のような文章になる。
SはPかつP'である。
犬は哺乳類かつ四足歩行である。
Dogs are mammals and quadrupeds.
2つの定言判断pとqを連結することもできる。
pかつq。
p∧q
犬は哺乳類である、かつ犬は四足歩行である。
Dogs are mammals, and dogs are quadrupeds.
「かつ」は論理学では記号「∧」もしくは「&」で表される。英語では「and」で表される。ベン図で書くと図1のようになる。

ベン図で考えると連言は「pかつq」はpとqの共通部分を表している。
並列(「および」)
「and」は連言の他に並列を表す場合がある。並列は日本語は「および」が相当する。
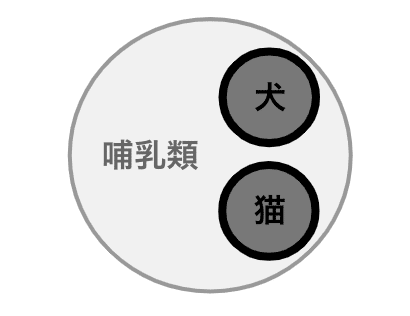
論理学的には連言と同じ意味であるが、少しニュアンスが異なる。「犬は哺乳類かつ四足歩行である」のように条件を絞り込むのではなく、「犬および猫は哺乳類である」のように独立した別個の主張を繋げるイメージだ(図2)。
Dogs and cats are mammals
犬および猫は哺乳類である。
連言の錯誤
概念を連言で結合すると、適用範囲は狭くなる。それは図1から明らかでだと思うが、うっかりそれを忘れてしまうことがある。以下の例を見てほしい。
リンダは三一歳の独身女性。ものをはっきり言うタイプで頭がよい。大学で哲学を専攻した。女性や民族の差別問題、社会正義の問題に強い関心をもっている。また反核デモにも参加していた。
さて、次の二つの記述のうち、リンダの現在の状況に関して、どちらの方がより確率が高いと判断できるだろうか。
a 彼女はいま、銀行に勤めている。
b 彼女はいま、銀行に勤めており、女性解放運動に熱心である。
なんとなく、bのほうが確率が高そうだと感じたかもしれない。
しかし、述語は連言で結ばれているため、bの確率は必ず低くなる。図3のようにベン図で書いてみるとよくわかるはずだ。bはaに従属している。

選言(「または」)
「または」の意味
彼が飼っているのは、犬または猫である。
He keeps a dog or cat.
「pまたはq」は「pとqのどちらか一方が成り立つ」という意味だ。もう少しくどい言い方をすると「pとqの少なくともどちらか一方が成り立つ」となる。言い方を変えると、pが成り立っていないときは常にqが成り立たなければならないし、qが成り立っていないときは常にpが成り立たなければならない。これは消去法の考え方で、推論でよく用いられる。
「pまたはq」をpとqに分解してみると以下のようになる。
1-1.pが真であるとき
⇒ 「pまたはq」が真である
1-2.qが真であるとき
⇒ 「pまたはq」が真である
2-1.「pまたはq」が真であるとき
⇒ 「pが偽」のとき「qが真」が成り立つ
2-2.「pまたはq」が真であるとき
⇒ 「qが偽」のとき「pが真」が成り立つ
pとqは両立する?〜強選言と弱選言の区別
彼が飼っているのは、犬または猫である。
He keeps a dog or cat.
再びこの主張はの意味を考えよう。
「犬と猫を両方飼うことができる」は同時にするだろうか?
それは、「または」の意味によって変わってくる、が答えである。
2つの選択肢のいずれか一方だけが真であって、共に真(偽)であることはないような選言は強選言と呼ばれる。排他的な選言(XOR: exclusive or)とも呼ばれる。
これに対して、2つの選択肢が共に真となりうる選言は弱選言と呼ばれる。非排他的な選言(and/or)とも呼ばれる。
厳密な議論の場合にはこれらを区別する必要がある。強選言であることを明示するには「AまたはBのいずれか」「either A or B」とする。
彼が飼っているのは、犬または猫のいずれかである。
He keeps either a dog or a cat.
弱選言であることを明示するには「AまたはB、またはその両方」「A or B, or both」(「and/or」とも書かれる)とする。
彼が飼っているのは、犬または猫、またはその両方である。
He keeps a dog or a cat, or both.
選言判断
選言「または」という言葉で主語Sが連結された文章は以下のようになる。このような判断のことを選言判断とよぶ。
SまたはS'はPである。
彼または彼女が犯人である。
He or she is the culprit.
「または」は論理学では記号「∨」で表される。英語では「or」で表される。ベン図で書くと図4のようになる。
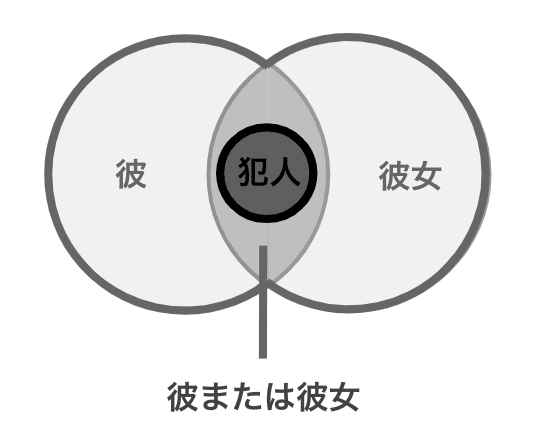
ベン図で考えると選言は「pまたはq」はpとqをあわせた領域を表している。
連言と同様に2つの定言判断pとqを連結できる。
pまたはq。
p∨q
彼が犯人である、または彼女が犯人である。
He is the culprit or she is the culprit.
命を張る以外ない?〜二分法の誤謬
選言判断では陥りがちな誤謬がある。以下のやりとりを見てほしい。


利根川の主張を丁寧に書くと以下のようになる。
努力ができぬ輩は、「命を賭けて2千万を得る」もしくは「2千万は夢のまた夢」かのいずれかである。
命を賭けるという究極のリスクを取るまでに2千万を得るための他の選択肢は思いつくはずだ。しかし利根川は迫真の演説でそれを見えなくしている。
同じような誤謬としては以下のようなものがある。
1.負け組になりたくなければ、勝ち組になるしかない!
2.かすみちゃんは僕の事を嫌いではないと言った。よって、かすみちゃんは僕のことが好きだ。
これは以下のような判断を前提としているが、これらはいずれも偽である。
1.人は「勝ち組である」もしくは「負け組である」のいずれかに一意に分類される。
2.かすみちゃんは僕のことが「好き」もしくは「嫌い」のいずれかである。
1は(定義次第ではあるが)人生なんて単純に勝ち組と負け組に分けられない。2は好きでも嫌いでもないケースが考えられる。
これは俗に「二分法」と呼ばれ、よく詭弁に用いられるので注意が必要だ。
仮言(「ならば」)
「ならば」の意味
「pならばq」は「pが成り立つ場合、qが成り立つ」という意味である。もう少しくどい言い方をすると「pが成り立つと仮定した場合、常にqが成り立つ」となる。ちなみに、対偶(参照:診察は論理的に誤り?〜対偶・必要十分条件〜中学生からの論理学入門 付録)を考えると「qが成り立たない場合、qが常に成り立たない」となる。これは背理法の考え方だ。
「pならばq」をpとqに分解してみると以下のようになる。
1.「pが真」を仮定して「qが真」が成り立つとき
⇒ 「pならばq」が真である
2.「pならばq」が真で、かつpが真であるとき
⇒ qが真となる
仮言判断
仮言「ならば」という言葉で定言判断pとqが連結された条件を表す文章は以下のようになる。このような判断のことを選言判断とよぶ。pは前件、qは後件とよばれる。
「ならば」は論理学では記号「⇒」で表される。英語では「If p, then q」で表される。
pならばq。
p⇒q
かすみちゃんが失恋するならば、かすみちゃんは悲しむ。
If Kasumi is heartbroken, then he is sad.
pとqは概念ではなく定言判断であるが、定言判断をまるごと概念Pと概念Qとみなせば(もしくは条件pと条件qを満たす集合Pと集合Qを考えれば)、ベン図を用いてわかりやすく可視化できる。仮言判断が真のとき、PとQは図7のような関係になっている。

生贄で厄災が収まる?
ある未開の村では「神に生贄を捧げると厄災が収まる」という迷信が信じられている。その村では過去に洪水や飢饉などの厄災に遭ったが、その度に神に生贄を捧げてきた。そうすると毎回、厄災が収まった。

「生贄を捧げるとその場合には必ず厄災が収まる」が真だとしよう。
しかし常識的に考えて生贄で厄災が収まるとは考えにくい。生贄など捧げても無意味なように思える。かわいそうだし。
だからこの村の人々に「生贄を捧げるのをやめよう!」と説得することにした。さて、どのように説得したらよいだろうか?
論理的に考えてみよう。「生贄を捧げると厄災が収まる」は仮言判断である。
「P=神に生贄を捧げるケース、Q=厄災が収まるケース」とすると、ケースPとQの関係は以下の図9のようになる。

「神に生贄を捧げるならば厄災が収まる」は赤の領域を示している。しかし、青の領域である「神に生贄を捧げなくても厄災が収まる」ケースが存在していることがわかるだろう。つまり、何もしなくても洪水などの厄災は時間が経てば勝手に収まっていた、すなわち「厄災が収まらない」ケースは存在しなかったというわけだ。
しかし、本当にこれで聞く耳を持ってもらえるだろうか? 「厄災が収まらない」ケースが存在しない保証などなく、もし厄災が収まらなかったら村が壊滅してしまう。そんなリスクは冒せない。
なのでこうするしかないだろう。

日常言語の曖昧さ
「そして」「および」などの接続詞は連言か並列どちらだろうか?
犬は動物そして/および哺乳類である。 (連言)
犬そして/および猫は動物である。 (並列)
このように、接続詞はかなり曖昧なので、正確なコミュニケーションが必要な場合は、「かつ」「または」「ならば」を使うことをすすめる。なお、法律文書は正確性を重視した文章のため、記法が統一されている。
両親が親権を放棄するか止められた場合は、家庭裁判所に未成年後見人を選任するように請求しなければならない。
この文章を法律の言葉で厳密に書くと以下のようになる。
父若しくは母が親権若しくは管理権を辞し、又は父若しくは母について親権喪失、親権停止若しくは管理権喪失の審判があったことによって未成年後見人を選任する必要が生じたときは、その父又は母は、遅滞なく未成年後見人の選任を家庭裁判所に請求しなければならない。
接続詞の意味問題
最後は以下の太字部分の接続詞が{連言、並列、強選言、弱選言、仮言}どれに相当するか考えて見てほしい。
本法律が制定されたことにより、劇場内での映画の撮影・録音は犯罪となります。
また、こうした盗撮映像のWEBでの公開、DVDの作成や販売も犯罪となります。盗撮行為に対する量刑は、10年以下の懲役、もしくは1,000万円以下の罰金、又は、その両方が科せられることとなります。
・劇場内での不審な行為を見かけましたら、劇場スタッフまでお知らせください。
・WEB上で盗撮映像のアップロードもしくは海賊版DVDの販売を見かけた場合は、通報にご協力をお願いしております。
解答
・や :並列 (=および)
・も :並列 (=および)
・もしくは :強選言(=または)
・又は、その両方:弱選言(=または)
・ら :仮言 (=ならば)
・もしくは :弱選言(=または)
・場合は :仮言 (=ならば)
「もしくは」が強選言と弱選言の2つの意味で使われていることがわかる。
他の接続詞もここに記しておこう。
・そして :連言 (=かつ)
・て :連言 (=かつ)
・しかし :連言 (=かつ)
・そして :並列 (=および)
・と :並列 (=および)
・ならびに :並列 (=および)
参考文献
鯵坂真、梅林誠爾、有尾善繁(1987)『論理学―思考の法則と科学の方法』世界思想社 第2章「伝統的形式論理学」
前回:定言判断
次回:対偶と必要十分条件
ここから先は
¥ 500
この記事が気に入ったらチップで応援してみませんか?
