正規分布、スターリングの公式、を初等的に導く (後編)

これが二項分布である。
当然だが、以下が成り立つ。

f(n,x)を縦に√n倍、横に1/√n倍したものが、Φ(n,x)であるのだから、Φ(n,x)のグラフの面積も、f(n,x)のグラフの面積と同じ1である。


ここから、以下の式が成り立ちそうな気がする。

これは実際に成り立つのだが、証明は後回しにして、取り敢えずこれが成り立つと仮定する。そうするとKが確定する。
まずよく知られた以下の式を導く。


ここから、ヤコブ行列式を使うことになる。

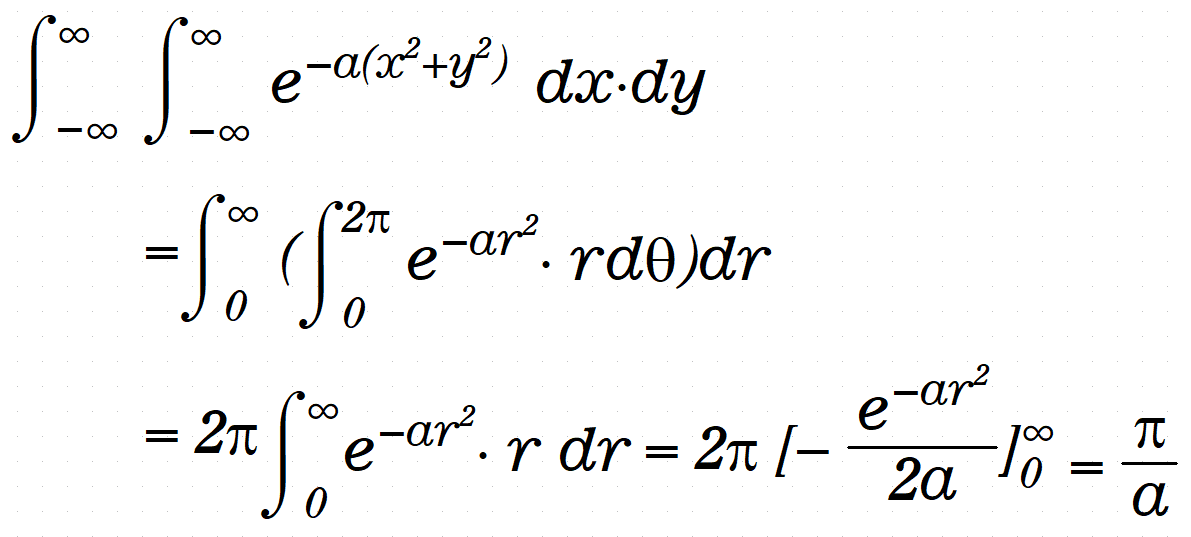
よって、以下が成り立つ。

そうすると、以下が成り立つ。
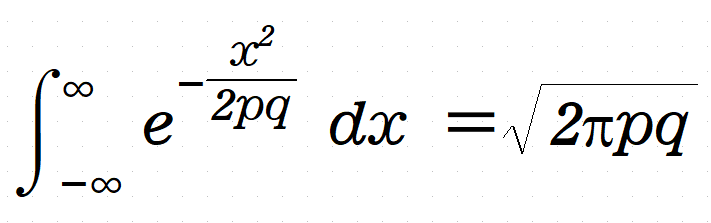
ここから、

となる。
(中編)の最後の方からわかるように

である。
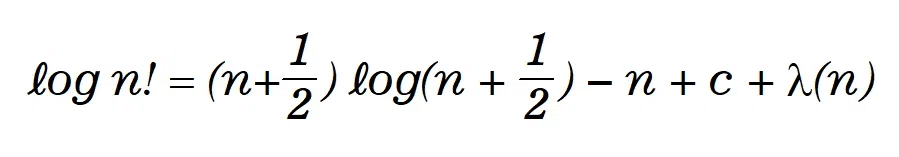
である。


これは、スターリングの公式に似ているがちょっと違う。


これによって、スターリングの公式が求められる。
まとめ

これが成り立つなら


が成り立つ。

の証明は、次回、完結編で
