正規分布、スターリングの公式、を初等的に導く (前編)
二項分布 正規分布 スターリングの公式
ずいぶん以前、正規分布というものに初めて遭遇した時に、これは二項分布の極限なんだろうな、と漠然と思ったが、具体的にどういう極限を取ればいいのかが分からなかった。

Aでnを∞に飛ばしても、Bにはならない。
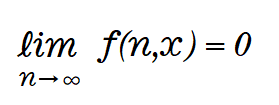
となってしまう。
あれこれ考えて、f(n,x)を縦方向に√n倍引き伸ばし、横方向を1/√n倍に縮小させれば、Φ(x)になることに気づいた。

これに関して、最初証明できたと思っていたが、よくよく検証すると厳密性を欠くものだった。その後、あれこれ考えて、多分証明できた(と思う)。
スターリングの公式 というのがあり、それを使うと証明できるが、スターリングの公式の証明には、ウォリスの公式というものを使うらしく、これもまた証明が必要で、・・・という具合である。
しかし、スターリングの公式を前提としないで証明することができ、逆にそこからスターリングの公式を導くことができた。

対数関数に関しての公式


が成り立つ。

を使えばすぐに示すことができる。このテイラー展開を示すのも容易。
敢えて使わないで、以下のように(ア)(イ)を導くこともできる。
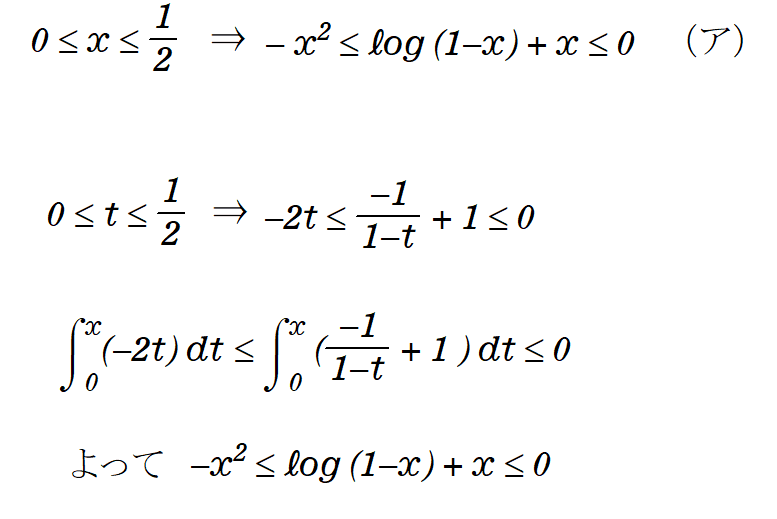
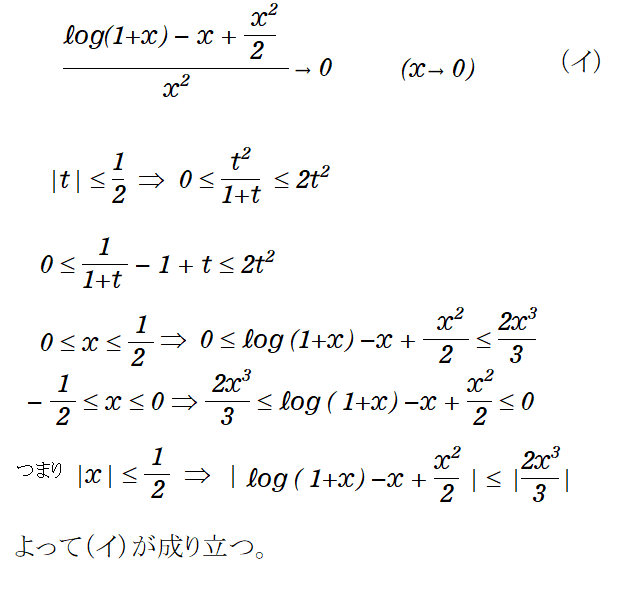
スターリングの公式 もどき の証明
以下を示す。

nを2以上の整数とする。





これは、以下のように書き表すこともできる。
ただし、cは何らかの実数。λ(n)は n→∞で 0に収束する何らかの数列。

