【Python】SP500の株価先行指数について(HYGについて)
株価を前もって予測できる指数はあるのでしょうか?先行して株価が上がるか下がるかがわかる指数があれば知りたいと思いませんか。
ここでは、S&P500の株価とハイイールド債(HYG)、Russel 2000、SKEW指数、VIX指数の関係を分析して、これらの指数が将来のS&P500の株価を予測できる可能性があるか確認します。
ハイイールド債(HYG)は、アメリカ株の先行指数として有名です。HYGはアメリカの低格付けの企業を集めたジャンク債ETFです。
Russel 2000は、米国小型株を集めた指数で、景気が悪くなると、小型株にまでお金が行き渡らなくなり、S&P500のような大型株より、先に低迷することが知られています。炭鉱のカナリアとして有名です。炭鉱のカナリアという言葉は、炭鉱で有毒ガスが発生した場合、人間よりも先にカナリアが察知して鳴き声をやむことから、その昔、炭鉱労働者がカナリアをかごに入れて坑道に入ったことに由来するそうです。
SKEWは、CBOE SKEW Index(CBOEスキュー指数)を表します。これは、市場参加者の長期的なリスクに関する見通しを提供する指数です。高いスキュー値は、大きな下落のリスクが増加していることを示唆します。
VIXは、CBOE Volatility Index(CBOEボラティリティ指数)を表します。これは、オプション市場のボラティリティを測定する指数であり、市場の恐怖心や不安のレベルを示すことで知られています。
これらの指数は、S&P500の株価の動きと相関があると言われており、過去の記事において、SKEWとVIXについてはある程度相関があることも確認しています。
https://note.com/scilabcafe/n/n91f21c5aa65b
今回はさらに深堀りし、ハイイールド債(HYG)に対して、日にちを前後にずらして相関係数を確認することで、ずらした日にちに対して相関係数をグラフにします。そして、相関が一番高いところがどこにあるかを確認することで、前もってこれらの指数を監視することで、S&P500の先行指数として使えるのを確認していきます。
なお、最低限のポイントのみの説明にするため、Pythonライブラリ、モジュール等のインストール方法については割愛させて頂きます。お使いのPC環境等に合わせてインストールしてもらえればと思います。
1.SP500とHYG、Russel 2000、SKEW、VIXを取得して推移を確認する
S&P500とHYG、Russel 2000、SKEW指数、VIX指数を取得するために、pandas-datareaderとyfinanceを使用します。取得する日付範囲と取得するコードを指定して、stooq および yfinanceより株価情報を取得します。
株価取得開始日:start = '2020-01-01'
株価取得終了日:end = datetime.date.today()(今日の日付を取得)
各種ライブラリをインポートします。
import pandas_datareader.data as web
import yfinance as yf
import datetime
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import gridspec
import japanize_matplotlib
%matplotlib inlineS&P500と各種指数のティッカーコードをリストに格納します。そして、現在の日時を最終日とし、2020-01-01を開始日として、stooq と yfinance からS&P500と各種指数を取得します。そして、stooq と yfinanceから取得したデータを結合します。
# stooqより取得
codelists_stooq = [
"^SPX", # SP 500
]
# yahoofinanceより取得
codelists_yf = [
'HYG', # ハイ・イールド債
'^RUT', # Russel 2000
"^SKEW", # SKEW
"^VIX", # VIX index
]
# 2020/1/1から現在まで
start = '2020-01-01'
end = datetime.date.today()
# データ取得(stooq)
_df_stooq = web.DataReader(codelists_stooq, 'stooq', start, end)['Close']
# 日付を昇順に並び替える
_df_stooq.sort_index(inplace=True)
# データ取得(yahoo finance)
_df_yahoo = yf.download(codelists_yf, start, end)['Close']
df = pd.DataFrame()
df = pd.merge(_df_stooq, _df_yahoo, on='Date', how='inner')
df.columns = ['SP500', 'HYG', 'Russel2000', 'SKEW', 'VIX']
display(df)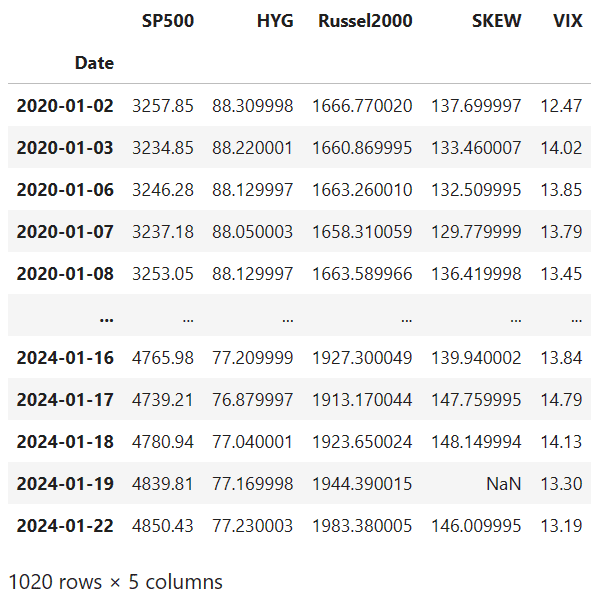
'^SPX':S&P500の株価指数
'HYG':ジャンク債
'^RUT':Russell 2000 Index(ラッセル2000指数)アメリカの中小型企業の株式のパフォーマンスを追跡する指数
'^SKEW':CBOE SKEW Index(CBOEスキュー指数)市場参加者の長期的なリスクに関する見通しを提供する指数。高いスキュー値は、市場の大きな下落のリスクが増加していることを示唆
'^VIX':CBOE Volatility Index(CBOEボラティリティ指数)オプション市場のボラティリティを測定する指数であり、市場の恐怖心や不安のレベルを示す
データフレーム df にNoneがないか、df.isnull().sum()で確認します。SKEWデータに 61 のNoneがあることが確認できます。
display(df.info())
print('-----------------------')
display(df.isnull().sum())
SKEWの NaNをNaNの前の値で補完します。再度 df.isnull().sum() でNaNがないことを確認します。
df['SKEW'].ffill(inplace=True) # NaNをNanの前の値で補完する
display(df.isnull().sum()) # NaNがないか再度確認する
次に簡単にデータを描画して確認します。
plt.figure(figsize=(14,16))
# 余白を設定
plt.subplots_adjust(wspace=0.4, hspace=0.6)
# グラフの描画
plt.subplot(5,1,1)
plt.plot(df['SP500'], label='SP500')
plt.title('SP500')
plt.legend()
plt.grid(True)
plt.subplot(5,1,2)
plt.plot(df['HYG'], label='HYG')
plt.title('HYG')
plt.legend()
plt.grid(True)
plt.subplot(5,1,3)
plt.plot(df['Russel2000'], label='Russel2000')
plt.title('Russel2000')
plt.legend()
plt.grid(True)
plt.subplot(5,1,4)
plt.plot(df['SKEW'], label='SKEW')
plt.title('SKEW')
plt.legend()
plt.grid(True)
plt.subplot(5,1,5)
plt.plot(df['VIX'], label='VIX')
plt.title('VIX')
plt.legend()
plt.grid(True)
plt.show()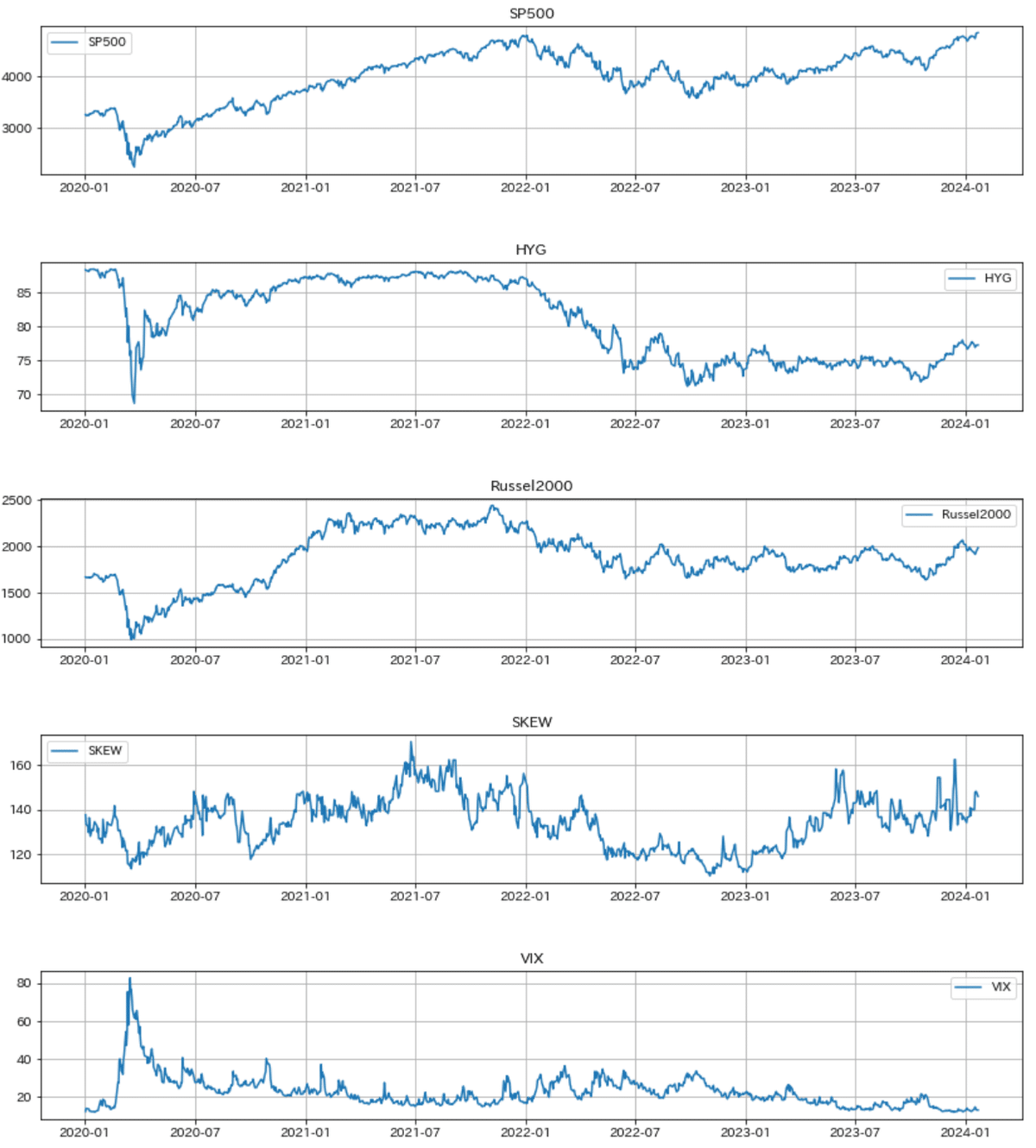
2.データの平滑化
データを平滑化するために、短期14日での単純移動平均(SMA:Simple Moving Average)をとります。
# 14日の移動平均をとる
df['SP500_SMA14'] = df['SP500'].rolling(window=14).mean()
df['HYG_SMA14'] = df['HYG'].rolling(window=14).mean()
df['Russel2000_SMA14'] = df['Russel2000'].rolling(window=14).mean()
df['SKEW_SMA14'] = df['SKEW'].rolling(window=14).mean()
df['VIX_SMA14'] = df['VIX'].rolling(window=14).mean()
display(df)
NaN を消去して、NaN がなくなったことを確認します。
df.dropna(how='any', inplace=True) # NaNを消去
display(df)
display(df.isnull().sum())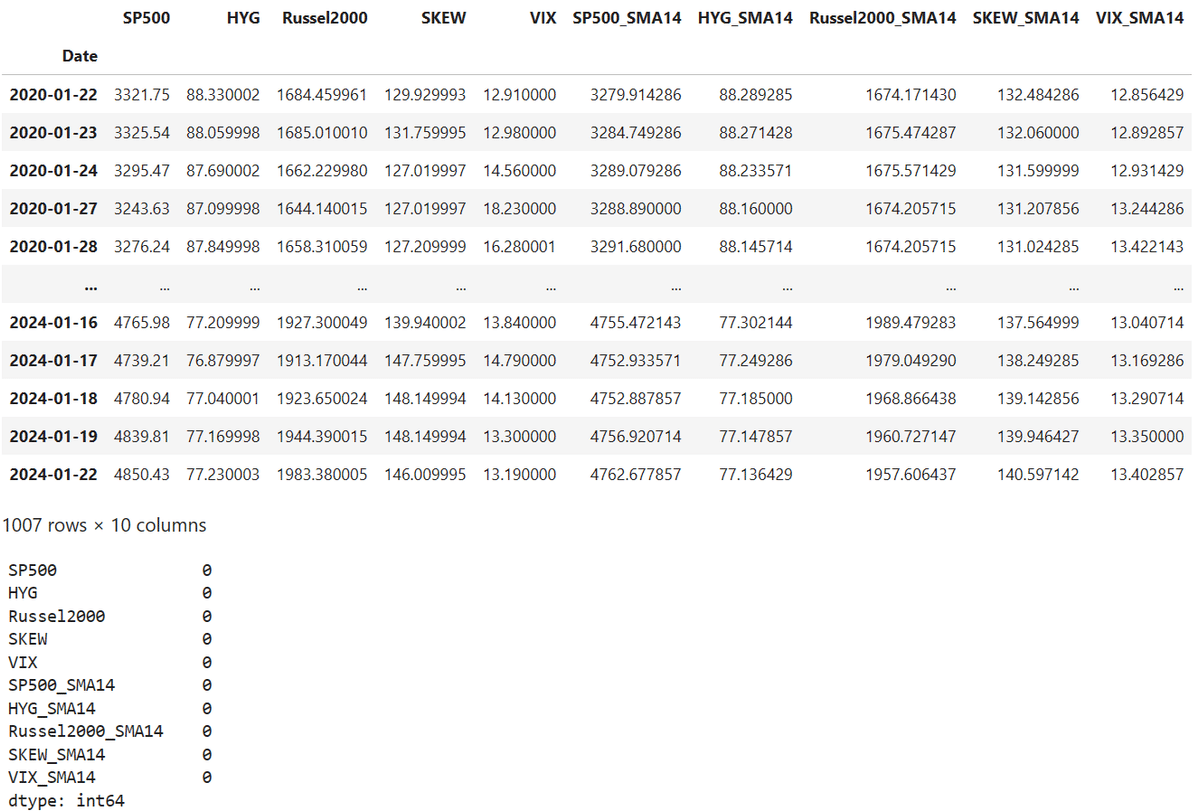
短期14日での単純移動平均(SMA:Simple Moving Average)のデータを描画して確認します。
plt.figure(figsize=(14,16))
# 余白を設定
plt.subplots_adjust(wspace=0.4, hspace=0.6)
# グラフの描画
plt.subplot(5,1,1)
plt.plot(df['SP500_SMA14'], label='SP500_SMA14')
plt.title('SP500_SMA14')
plt.legend()
plt.grid(True)
plt.subplot(5,1,2)
plt.plot(df['HYG_SMA14'], label='HYG_SMA14')
plt.title('HYG_SMA14')
plt.legend()
plt.grid(True)
plt.subplot(5,1,3)
plt.plot(df['Russel2000_SMA14'], label='Russel2000_SMA14')
plt.title('Russel2000_SMA14')
plt.legend()
plt.grid(True)
plt.subplot(5,1,4)
plt.plot(df['SKEW_SMA14'], label='SKEW_SMA14')
plt.title('SKEW_SMA14')
plt.legend()
plt.grid(True)
plt.subplot(5,1,5)
plt.plot(df['VIX_SMA14'], label='VIX_SMA14')
plt.title('VIX_SMA14')
plt.legend()
plt.grid(True)
plt.show()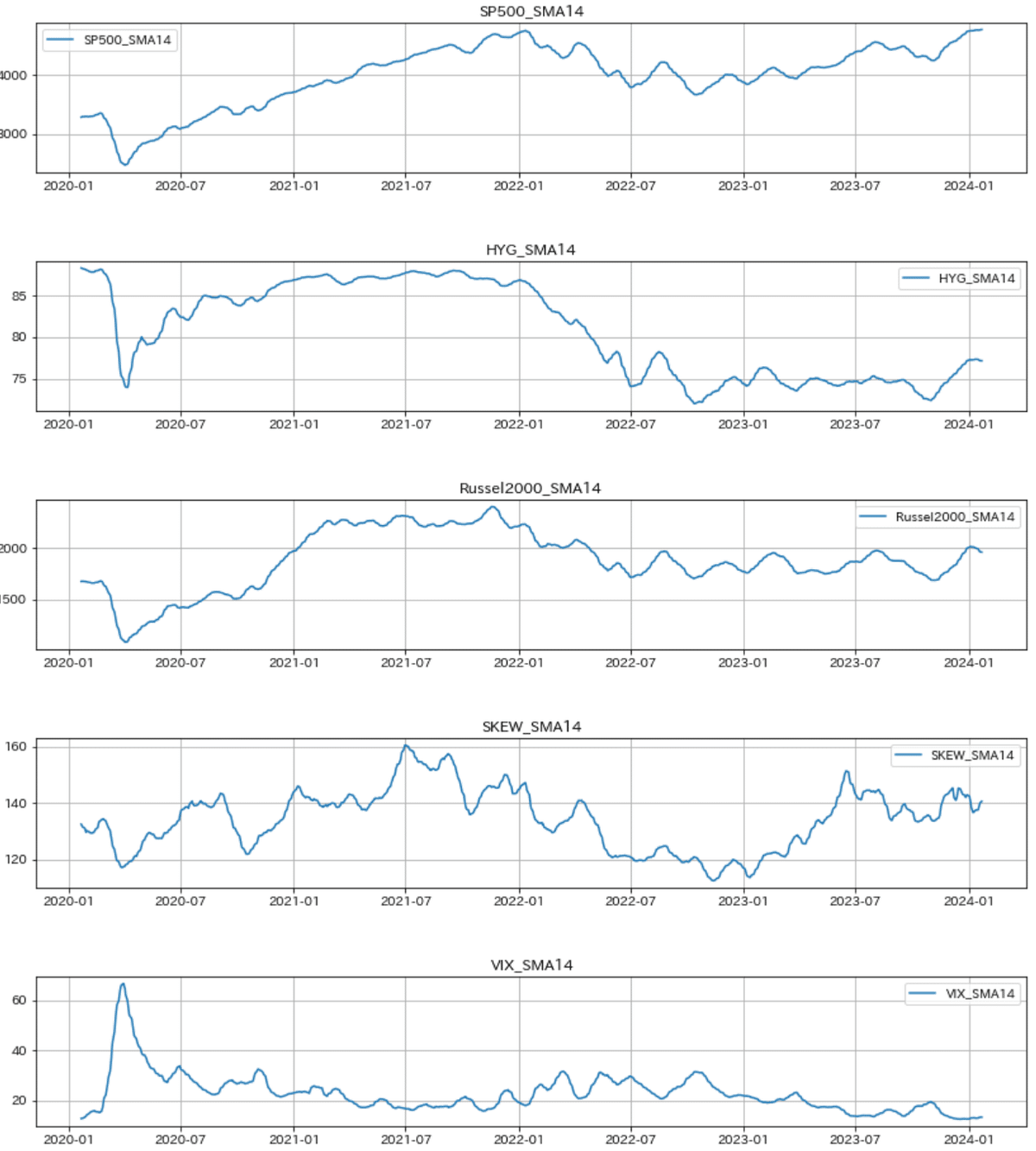
以降、平滑化したデータフレーム df を用いて詳細な分析をしていきます。
3.S&P500とHYGの時系列のグラフ作成
S&P500とHYGのグラフを重ねて表示することで、両者の関係を大雑把に確認してみます。ここでは、plotly を使って可視化していきます。
S&P500とHYG共に、短期14日の単純移動平均(SMA:Simple Moving Average)のデータを使います。
import plotly.graph_objects as go # グラフ表示関連ライブラリ
import plotly.io as pio # 入出力関連ライブラリ
pio.renderers.default = 'iframe'
# subplot
from plotly.subplots import make_subplots
# グラフの実体trace オブジェクトを生成
sp500_trace = go.Scatter(
x=df.index,
y=df['SP500_SMA14'],
mode='lines',
line=dict(color='blue', width=5),
name='SP500_SMA14'
)
# グラフの実体trace オブジェクトを生成
hyg_trace = go.Scatter(
x=df.index,
y=df['HYG_SMA14'],
mode='lines',
line=dict(color='red', width=5),
name='HYG_SMA14'
)
# 2つ目の軸を表示する設定
fig = make_subplots(specs=[[{"secondary_y": True}]])
# 描画領域である figure オブジェクトの作成
fig.add_trace(sp500_trace, secondary_y=False) # 第1軸に設定(secondary_y=False)
fig.add_trace(hyg_trace, secondary_y=True) # 第2軸に設定(secondary_y=True)
# レイアウトの更新
fig.update_layout(
# 凡例
showlegend=True,
# 幅と高さの設定
width=900,height=600,
# タイトルの設定
title=dict(
text='SP500とHYGの関係', # タイトル
font=dict(family='Times New Roman', size=20, color='grey'), # フォントの指定
xref='paper', # container or paper
x=0.45,
y=0.9,
xanchor='center',
),
plot_bgcolor='white', # 背景色を白に設定
# 凡例の設定
legend=dict(
xanchor='right',
yanchor='bottom',
x=0.5,
y=0.85,
orientation='v',
bgcolor='white',
bordercolor='grey',
borderwidth=1,
),
),
# 軸の設定
fig.update_yaxes(title='SP500', secondary_y=False)
fig.update_yaxes(title='HYG', secondary_y=True)
# linecolorを設定して、ラインをミラーリング(mirror=True)して枠にする
fig.update_xaxes(linecolor='black', linewidth=1, mirror=True)
fig.update_yaxes(linecolor='black', linewidth=1, mirror=True)
fig.update_xaxes(linecolor='black', linewidth=1, mirror=True)
fig.update_yaxes(linecolor='black', linewidth=1, mirror=True)
# ticks='inside':目盛り内側, tickcolor:目盛りの色, tickwidth:目盛りの幅、ticklen:目盛りの長さ
fig.update_xaxes(ticks='inside', tickcolor='black', tickwidth=1, ticklen=5)
fig.update_yaxes(ticks='inside', tickcolor='black', tickwidth=1, ticklen=5)
fig.update_xaxes(ticks='inside', tickcolor='black', tickwidth=1, ticklen=5)
fig.update_yaxes(ticks='inside', tickcolor='black', tickwidth=1, ticklen=5)
# gridcolor:グリッドの色, gridwidth:グリッドの幅、griddash='dot':破線
fig.update_xaxes(gridcolor='lightgrey', gridwidth=1, griddash='dot')
fig.update_yaxes(gridcolor='lightgrey', gridwidth=1, griddash='dot')
fig.update_xaxes(gridcolor='lightgrey', gridwidth=1, griddash='dot')
fig.update_yaxes(gridcolor='lightgrey', gridwidth=1, griddash='dot')
# tick0:初期軸目盛り, dtick:軸目盛り間隔
fig.update_xaxes(dtick='M12') # 12カ月ごと
# 軸の文字サイズ変更
fig.update_xaxes(tickfont=dict(size=14, color='grey'))
fig.update_yaxes(tickfont=dict(size=18, color='grey'))
# show()メソッドでグラフを描画
fig.show()
S&P500とHYGの間には、相関がありそうです。2021年の後半でのHYGの下落が、S&P500に先行しているようにも見えます。そこで、これらのデータの詳細な相関分析をおこなっていきます。
4.S&P500とHYGの詳細な相関分析
4-1.前処理
S&P500とHYGのみのデータフレーム df_SP500_HYG を作成して、更に、HYGを-60から60日ずらしたデータを作成して、df_SP500_HYG に結合します。
# SP500とHYGのみのデータフレームを作成
df_SP500_HYG = df[['SP500', 'HYG_SMA14']]
display(df_SP500_HYG)
# List of days to shift from -60 to 60
shift_days = list(range(-60, 61))
for days in shift_days:
# Determine the suffix for column names
suffix = 'B' if days < 0 else 'A' if days > 0 else 'Current'
# Create a shifted dataframe
shifted_df = df_SP500_HYG[['HYG_SMA14']].shift(freq=f'{days}D')
# Rename the column
shifted_df.columns = [f'HYG_{abs(days)}D_{suffix}']
# Merge with the main dataframe
df_SP500_HYG = pd.merge(df_SP500_HYG, shifted_df, on='Date', how='left')
display(df_SP500_HYG)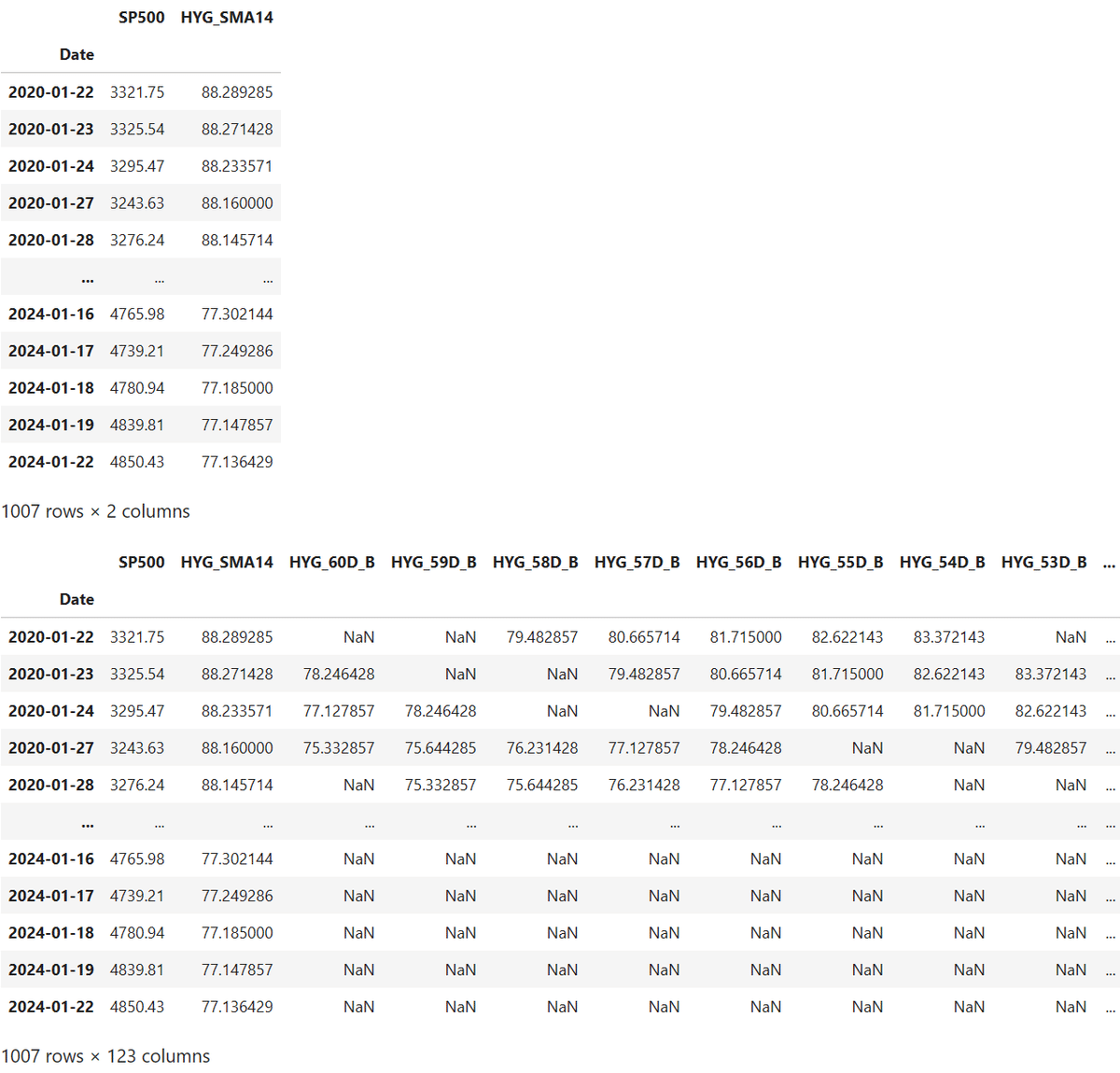
df_SP500_HYGの NaNをNaNの前の値で補完します。df_SP500_HYG.isnull().sum() でNaNがないことを確認します。
df_SP500_HYG.ffill(inplace=True) # NaNをNanの前の値で補完する
display(df_SP500_HYG.isnull().sum()) # NaNがないか確認する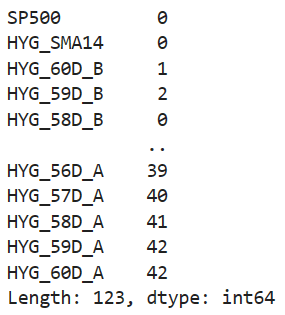
NaNがあるので消去します。
df_SP500_HYG.dropna(how='any', inplace=True) # NaNを消去
display(df_SP500_HYG.isnull().sum()) # NaNがないか確認する
display(df_SP500_HYG)
4-2.SP500とHYGを-60から60日ずらしたデータとの相関係数を算出して描画
S&P500とHYGを-60から60日ずらしたデータとの相関係数を算出します。
df_SP500_HYG.corr() # 相関関係
S&P500との関係を抽出するため、SP500列のみを新たなデータフレーム df_SP500_HYG_corr とします。
df_SP500_HYG_corr = df_SP500_HYG.corr()[['SP500']] # 相関係数の SP500の列のみをデータフレームにする
df_SP500_HYG_corr.drop(index='SP500', inplace=True) # indexの SP500の行を削除
df_SP500_HYG_corr.reset_index(inplace=True) # indexをリセットする
df_SP500_HYG_corr.columns = ['スライド日数_元', '相関係数']
df_SP500_HYG_corr.drop(index=0, inplace=True) # HYG_SMA14の行を削除する
display(df_SP500_HYG_corr)
-60から60日ずらした日数と相関係数の関係を可視化するために、ずらした日数、すなわちスライド日数列を新たに作成します。
df_SP500_HYG_corr['スライド日数'] = 0
# List of days to shift from -60 to 60
shift_days = list(range(-60, 61))
for days in shift_days:
# Determine the suffix for column names
suffix = 'B' if days < 0 else 'A' if days > 0 else 'Current'
# column name
shifted_colum_name = f'HYG_{abs(days)}D_{suffix}'
df_SP500_HYG_corr.loc[df_SP500_HYG_corr['スライド日数_元'] == shifted_colum_name, 'スライド日数'] = days
display(df_SP500_HYG_corr)
スライド日数と相関係数の関係をグラフで可視化します。
# グラフの実体trace オブジェクトを生成
bar_trace_1 = go.Bar(x = df_SP500_HYG_corr['スライド日数'], y = df_SP500_HYG_corr['相関係数'], name = '相関係数')
# レイアウトオブジェクトを生成
graph_layout = go.Layout(
# 幅と高さの設定
width=800, height=600,
# タイトルの設定
title=dict(
text='スライド日数と相関係数の関係', # タイトル
font=dict(family='Times New Roman', size=20, color='grey'), # フォントの指定
xref='paper', # container or paper
x=0.5,
y=0.87,
xanchor='center',
),
# 軸の設定
xaxis = dict(title = 'スライド日数', showgrid=False),
yaxis = dict(title = '相関係数', side = 'left', showgrid=False),
# yaxis2 = dict(title = '相関係数', side = 'right',showgrid=False, overlaying = 'y'),
# 凡例の設定
legend=dict(
xanchor='left',
yanchor='bottom',
x=0.5,
y=0.85,
orientation='h',
bgcolor='white',
bordercolor='grey',
borderwidth=1,
),
)
# 描画領域である figure オブジェクトの作成
fig = go.Figure(layout=graph_layout)
# add_trace()メソッドでグラフの実体を追加
fig.add_trace(bar_trace_1)
# fig.add_trace(scatter_trace_1)
# レイアウトの更新
fig.update_layout(
plot_bgcolor='white', # 背景色を白に設定
)
# 軸の設定
# linecolorを設定して、ラインをミラーリング(mirror=True)して枠にする
fig.update_xaxes(linecolor='black', linewidth=1, mirror=True)
fig.update_yaxes(linecolor='black', linewidth=1, mirror=True)
# ticks='inside':目盛り内側, tickcolor:目盛りの色, tickwidth:目盛りの幅、ticklen:目盛りの長さ
fig.update_xaxes(ticks='inside', tickcolor='black', tickwidth=1, ticklen=5)
fig.update_yaxes(ticks='inside', tickcolor='black', tickwidth=1, ticklen=5)
# gridcolor:グリッドの色, gridwidth:グリッドの幅、griddash='dot':破線
fig.update_xaxes(gridcolor='lightgrey', gridwidth=1, griddash='dot')
fig.update_yaxes(gridcolor='lightgrey', gridwidth=1, griddash='dot')
# 軸の文字サイズ変更
fig.update_xaxes(tickfont=dict(size=15, color='grey'))
fig.update_yaxes(tickfont=dict(size=15, color='grey'))
# show()メソッドでグラフを描画
fig.show()
今回はハイイールド債(HYG)に対して、日にちを前後にずらして相関係数を確認することで、前もってHYGを監視することで、S&P500の株価の上昇もしくは下降を予測できないか検討しましたが、スライド日数 0 近辺、すなわち一致して動いているときが一番S&P500の株価との相関が大きい結果となりました。今後は、他の指標についても同様の手法で、先行指数があるのかを確認していきたいと思います。
