
電子はいかにして化学結合をもたらすか
※本稿は高校生、および大学学部1,2年生向けです。
本稿の要約
原子核同士のクーロン斥力と原子核間に存在する電子によるクーロン引力とのバランスによって化学結合は成立している。
初めに
有機化学、それは大雑把にいってしまえば化学結合の組み換えを研究する学問です。多くの化学者がいかにして今ある化学結合を組み換え新しい化学結合を構築するか、そしてそれによって新たな物質を生み出すかを日夜追い求めています。有機化学に限らず、化学全般の分野において『化学結合』というものは極めて重要な概念です。にもかかわらず、なぜこの化学結合が成立するのかをきちんと説明できる人は案外多くありません。それどころか、ほとんどの教科書や参考書において「原子核同士が電子によって結ばれることで結合が生じる」といったようなことが当たり前のように書いてあり、ではそもそもなぜ原子核間に電子が存在すると結合が成立するのかの説明が省略されていることがほとんどなように感じています。そこで本稿ではその「化学結合の起源」について、クーロン相互作用の観点から簡易的かつ定性的に紹介することを目的としています。基本的な内容としては高校レベルの物理知識があれば十分に理解できる話かと思います。
原子を構成する3要素
化学結合についての話に移る前に、まずは基本中の基本である原子の構造について復習です。原子はざっくり以下に示す3要素によって構成されています。
①陽子
陽子は原子核構成成分の一つで+の電気素量(電荷) を有する粒子です。
②中性子
中性子は原子核構成成分の一つでその名の通り電気的に中性の粒子です。
③電子
電子は原子核の周囲に存在する-の電気素量(電荷) を有する素粒子です。
まぁここら辺は中学理科の復習なので流石に大丈夫でしょう。この3成分の中で今回の話で必要なのは陽子と電子なので中性子君の出番はここで終わりです。なお、本稿では議論を簡単にするために各成分は基本的に全て粒子として取り扱うこととします。
『余談』
陽子と中性子は合わせて核子とも呼ばれていますが、大体の人は初めて中性子のことを知った時に「君、いる?」と思ったんじゃないかと思います。まぁ中性子君の仕事っぷりについては、大学で核物理学か素粒子物理学でもとらないと詳細を学ぶことがないので仕方ないんですが(一般化学で軽く触れる先生はいるかも)。しかし中性子は原子核の安定に極めて重要な要素で、簡単にいうと陽子同士を結び付ける役割を担っています。原子核という非常に狭い領域に密集している陽子は、中性子がないとクーロン反発によってあっという間にバラバラになってしまいます。電気的に中性な中性子になぜそんなことができるかというと、中性子と陽子は相互変換が可能でありその変換の際にπ中間子を介して自然界の4つの力の一つである『強い力』という強力な引力が……長くなるのでやめましょうか。詳細が気になる方は「中間子理論」や「π中間子」で検索検索ぅ、です。
化学結合の起源
さて、ではここからは原子核(陽子) と電子の関係性について考えていきます。今回は話を簡単にするために2個の原子核(陽子)A,B が化学結合を形成する単純な系について考えてみましょう。その場合、次の三つのケースについてそれぞれ考えられます。
①2個の陽子のみで電子が存在しない場合
まずは陽子のみで電子が存在しない場合について考えてみます。その場合Fig.1に示すように+の電荷をもつ陽子同士にはクーロン反発が生じますので両者は反対方向に離れていってしまいます。当然このような状況では陽子Aと陽子Bは結合のしようがありません。

つまり、電子が存在しない場合は原子間に化学結合が生じないということになります。
※注
核力が生じるレベルまで陽子同士を近づければ引力的相互作用が発現しますがそれは核融合だし化学結合ではない。
②2個の陽子の中間に電子が存在する場合
では陽子A-Bの中間に電子が存在するとどうなるでしょうか。この場合は、Fig.2のように陽子には別の陽子との間のクーロン斥力と電子との間のクーロン引力が生じており、電子には2個の陽子からのクーロン引力が生じていることになります。

さて、ではここでクーロンの法則を思い出しましょう。クーロンの法則とは荷電粒子間に働く相互作用に関する法則であり、以下の式で表されます。
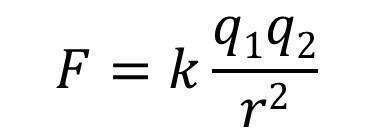
kは比例定数、q1,q2は荷電粒子1,荷電粒子粒子2の電荷量、rは荷電粒子間距離です。これをFig.2の系に適用してみましょう。陽子と電子はそれぞれ電気素量に相当する電荷量を持っていますから電荷量qは同じです。一方距離rは大きく異なります。電子は2つの陽子の中間にあるので、電子-陽子間の距離は陽子A-陽子B間の距離の1/2になります。クーロンの法則より荷電粒子間相互作用は距離の2乗に反比例するので、電子-陽子間のクーロン引力は陽子A-陽子B間のクーロン斥力より 1/(1/2)^2倍、すなわち4倍大きくなります。つまり、陽子に働く力は相手の陽子から遠ざかる方向に働く斥力より、電子を介して相手の陽子の方へ引かれる引力の方が4倍大きいことがわかります。また、中間にある電子は2つの陽子から大きさが等しく方向が逆な引力を受けるので、電子に働く力はたがいに打ち消しあいます。結果、電子は陽子A-陽子Bの中間にとどまり、2つの陽子はともに中央の電子の方に引き寄せられることになるのです。ただし、2つの陽子がある程度の距離まで電子に近づくと今度は陽子-陽子間のクーロン反発が無視できなくなるので際限なく近づいていくということにはなりません。どこかでこの電子-陽子間のクーロン引力と陽子-陽子間のクーロン斥力が丁度釣り合ったとき、それが化学結合の成立でありその距離が結合距離となるわけです。
③2個の陽子の外側に電子が存在する場合
さて、②より2個の陽子の間に電子を置くことで実質陽子間に引力的相互作用(結合) がもたらされることが分かりました。では電子が陽子A-陽子Bの中間領域から離れた位置、Fig.3のような位置に存在する場合はどうなるでしょうか。

陽子Aと陽子Bはともに電子の方向に引かれていきますが、電子の近くにある陽子Aに働くクーロン引力が遠い陽子Bに働くクーロン引力よりもはるかに大きくなるので2つの陽子間の距離は次第に大きくなっていきます。すなわち、陽子Aと陽子Bには相対的に離れようとする方向の力がもたらされることになります。なので陽子A-B間に結合は生じません。
以上①~③をまとめるとFig.4のような図になります。

Fig.4の結合性領域に電子が存在する場合、陽子間には引力的相互作用が働くため化学結合が成立する。一方、電子自体が存在しない、もしくは反結合性領域に電子が存在する場合は陽子間に引力的相互作用が働かないため結合が成立しない。というわけです。
このように、単純なクーロンの法則を用いることによって、化学結合が陽子(原子核) の中間領域に電子が存在することで成立しているということを簡単に示すことができます。何も難しいことはないんですが、高校化学でここら辺まで踏み込んで化学結合について教えることはほぼ無いんじゃないんですかねぇ※。
※注意
少なくとも著者が高校時代に聞いた記憶がないというだけで著者が話を聞いていなかっただけとか今は教えているよとかあるかもしれませんのであしからず。
まとめ
原子核にとって別の原子核は友達の友達。共通の友人である電子君が間にいるときは仲良くできるが、そうじゃないときは気まずくなってスマホをいじりだしがちだぞ。
以降余談というか補足というか
以上の話は極めて単純なモデルを採用しての説明になっていますが、化学結合の形成は現実にはもうちょい複雑です。
・原子核に働く相互作用を古典的なクーロン相互作用で論じていいのか
本稿で示したモデルでは電子を完全に粒子として扱っていますが、実際には粒子は波動性を有しておりまた特定の位置に静止することはなくしかもしれを追跡することもできません。ただし、量子力学的な計算によって、電子が空間上のどのような領域にどのような確率で存在しているかという情報(電子密度) は求めることができます。このような量子力学的世界において、本稿のようにいたって古典的なクーロン相互作用の考え方を使って化学結合を論じていいのでしょうか。
ここで、ある一つの重要な定理を紹介しましょう。それはHellmann–Feynmanの静電定理というものです。これは以下のようなものです。
Hellmann–Feynmanの静電定理
分子内の原子核Aの位置を微小変化させたとき、原子核Aに働く力は分子内の電子密度分布ρから受けるクーロン引力と他の原子核から受けるクーロン斥力を全て積算したものに等しい。
この定理の導出や証明は参考文献に委ねます。この定理の重要な点は、原子核の位置と電子密度分布さえわかれば、各原子核に働いている力は古典的なクーロン相互作用を使って求めることができるということを示している点です。なので本稿で用いたような単純なモデルで十分化学結合の起源を表わせられるわけです(いささか単純化しすぎですが)。
・化学結合時の原子核間クーロン反発の起源は
『陽子がある程度の距離まで電子に近づくと今度は陽子-陽子間のクーロン反発が無視できなくなるので際限なく近づいていくということにはなりません。』
ここについて軽く補足します。中性原子AとBが接近し原子オービタル同士が相互作用して結合性分子オービタルを形成、そこへ電子が収容されることでA-Bの化学結合が成立した場合を考えます。この時、A-B間に分布している電子密度がAの原子核とBの原子核を引き付けることで結合を作っているわけですが、本稿に書いたように原子核Aと原子核Bが際限なく近づいていくことにはなりません。共有結合の場合もともとAもBも電気的には中性なわけですが、これは原子核の+電荷をその周りに点対称的に分布している電子の-電荷で相殺(遮蔽といいます) しているためです。これはすなわち、実質的に原子オービタル上の電子は原子核に対して力を与えていないとも言えます。一方結合が生じる、すなわちA-B間に電子密度が分布するということは、原子核近傍の電子密度の減少をもたらします。その結果、遮蔽が不完全となり原子核の+電荷が漏れ出るような状態になってしまうため、他の原子核との間にクーロン斥力が生じてしまうわけです。直感的にも確かにそうなりそうな気がしますよね。
参考文献
[1] 中辻博 , 化学 , 1973, 28(1), 17-27
