
曲げモーメントを応力度に変換する断面係数
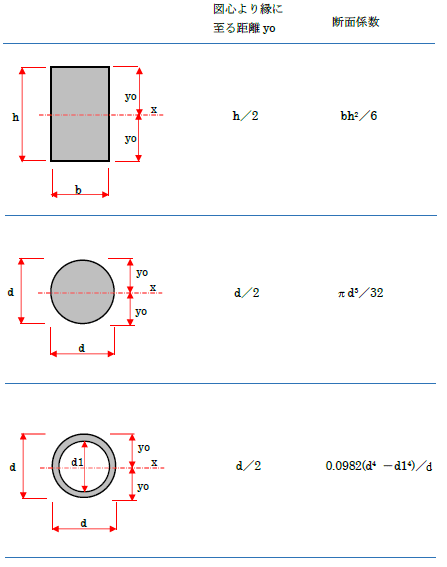
曲げモーメントを応力度に変換する断面係数Z
断面係数Zとは簡単に言えば、「曲げモーメントにどれだけ抵抗できるか?」示す値です。
$$
Z=\frac {BH^2} 6
$$
何となく暗記していましたが、今回はなぜこうなるかを研究してみます。
ある板に曲げモーメントMがかかった時

断面内部には 引張られる力 と 圧縮される力 が発生します。
この状況はシーソーに三角形の物体が乗った状況とみることができます。

三角形の端っこをσとすると、シーソーに加わる力は三角形の面積となる

シーソーの中心から三角形の重心までの距離は H/3

シーソーに加わる力 に 三角形の重心までの距離を乗じた 2個分の力は曲げモーメントと同じとなる

式を整理すると 6が出現

σを求める式に変換すると M を
$$
\frac {H^2} 6
$$
で除している式が出来上がりました。

最後にシーソーの奥行Bを考慮したら断面係数Z の 公式の出来上がり

結論
$$
Z=\frac {BH^2} 6
$$
は三角形の面積と重心位置でできている!!

