算数6年サピックス　デイリーサポート解説［61-16和と差に関する問題］

今回は和と差に関する問題ですが、和と差に気付くには問題文を読んで自分で面積図やてんびん、表、式などに整理することが大切です。

解説を参考に、自分で手を動かしてまとめてみましょう。

★解説を読んでも分からない、授業中に板書を写せないお子様に。テキスト付属の解説はとても簡易的です。そこで家庭学習でお子様が取り組まれるデイリーサポート［実践編A〜E］について、お子様が1人で取り組めるような補助教材を作成しました。

・確認編全問対応
・豊富なカラー図表
・計算の過程も分かる

★著作権の関係で問題文そのものは掲載しておりません。万一誤字脱字、ご要望などございましたらコメント欄にお願いいたします。対応教材は順次増やしていく予定です。

---

今回学ぶこと

• アプローチ$${\textcircled{\small{1}}}$$平均点を求める→A$${\fbox{2}}$$、平均算→C$${\fbox{2}}$$

• アプローチ$${\textcircled{\small{2}}}$$3種類の品物の値段→B$${\fbox{3}}$$、上茶と下茶→C$${\fbox{1}}$$

• アプローチ$${\textcircled{\small{3}}}$$3種類のゲーム→B$${\fbox{4}}$$、問題が3問→E$${\fbox{1}}$$

• アプローチ$${\textcircled{\small{4}}}$$2つの条件を整理する→A$${\fbox{5}}$$、範囲を考える→D$${\fbox{3}}$$

• アプローチ$${\textcircled{\small{5}}}$$階段でじゃんけん→C$${\fbox{3}}$$、差をとらえる→D$${\fbox{2}}$$

• アプローチ$${\textcircled{\small{6}}}$$3段つるかめ算(1)→C$${\fbox{4}}$$、3段つるかめ算(2)→D$${\fbox{1}}$$

• アプローチ$${\textcircled{\small{7}}}$$くるった巻尺(1)→D$${\fbox{4}}$$、くるった巻尺(2)→E$${\fbox{3}}$$

• アプローチ$${\textcircled{\small{8}}}$$条件を読みとる→E$${\fbox{2}}$$、5つの整数→E$${\fbox{4}}$$

復習テキスト

• H51-02和と差に関する問題、510−31和と差に関する問題

実践編A

$${\fbox{1}}$$

・等差数列の和：(最初+最後)×個数÷2

1,4,7,10,13,16,19の7個の数の和は、3ずつ増える等差数列の和で求められます。7個の数の和は1+4+7+10+…+19＝(1最初+19最後)×7個個数÷2＝70です。

引いた数を⬜︎として式を立てます。引いた数をのぞく6個の数の和は70−⬜︎で、ここから⬜︎を引くと(70−⬜︎)−⬜︎＝70−⬜︎×2です。

これが56になったということは、⬜︎×2＝14です。

$${\fbox{2}}$$平均点を求める

AとBの点数の和が126点ということは、A,B2人の平均点は126点÷2人＝63点です。

「A,B2人の平均点とC,D,E3人の平均点」の平均が「A,B,C,D,E5人の平均点」です。面積図またはてんびんで考えます。

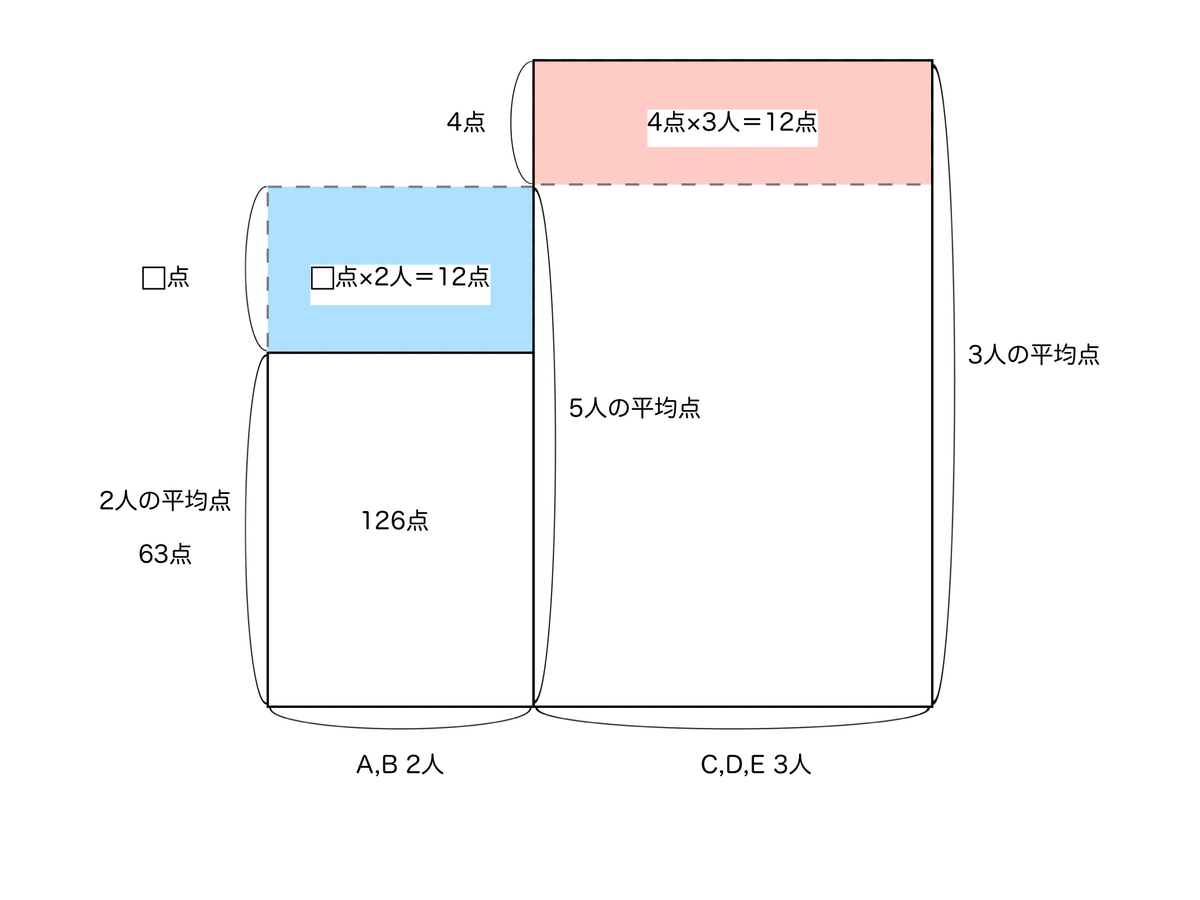
・面積図

青い長方形と赤い長方形の面積は等しいです。
⬜︎点×2人左側＝4点×3人右側より、⬜︎＝6
よって、5人の平均点はA,B2人の平均点の63点より6点高いです。

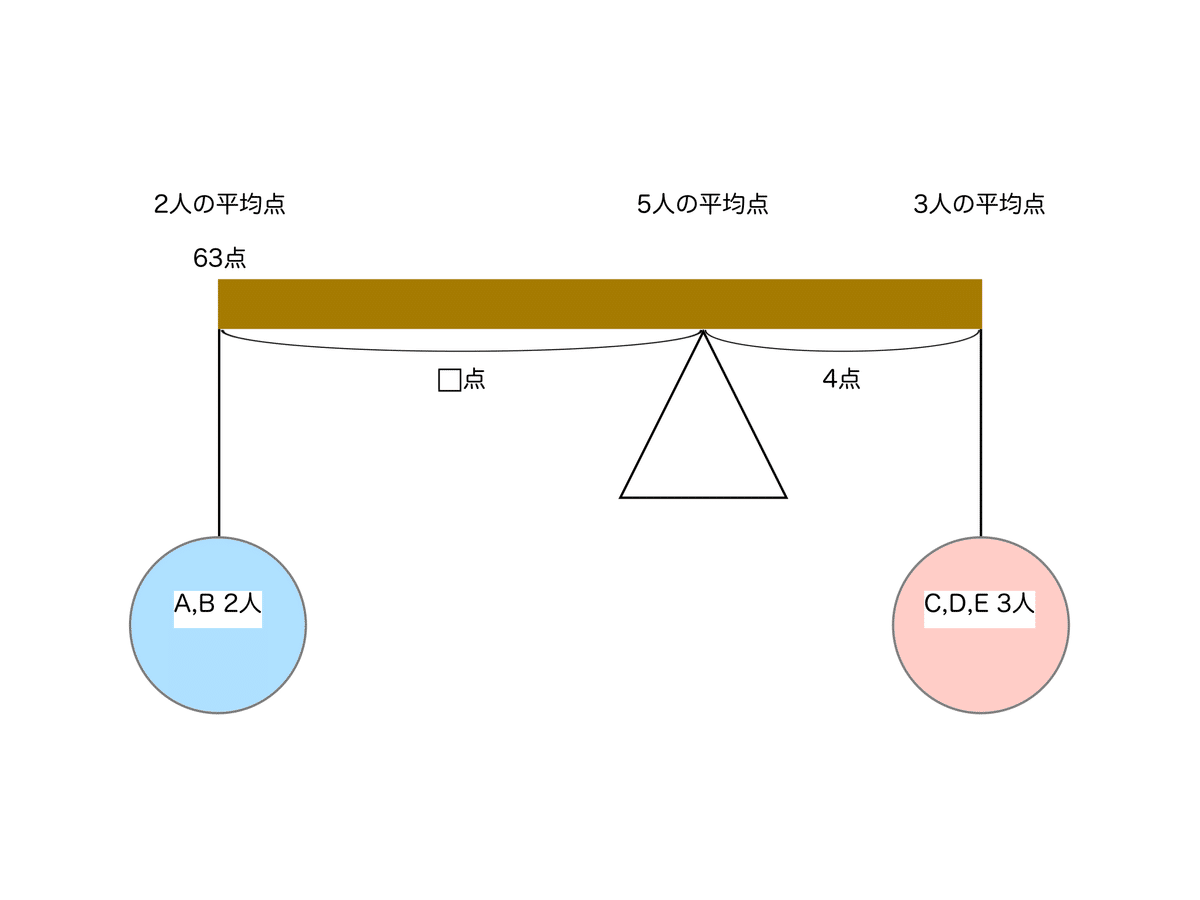
・てんびん

てんびんの左側と右側のつり合いを考えます。
⬜︎点×2人左側＝4点×3人右側より、⬜︎＝6
よって、5人の平均点はA,B2人の平均点の63点より6点高いです。

$${\fbox{3}}$$

はじめは箱の中に赤玉と白玉が同じ数だけ入っているので、個数の差は0個です。そこから1回に赤玉8個、白玉13個を同時に取り出していくと、箱の中に残っている赤玉と白玉の個数の差は5個ずつ開いていきます。

赤玉と白玉の個数の差が49個−4個＝45個になるのは、45個÷5個＝9回取り出したときです。

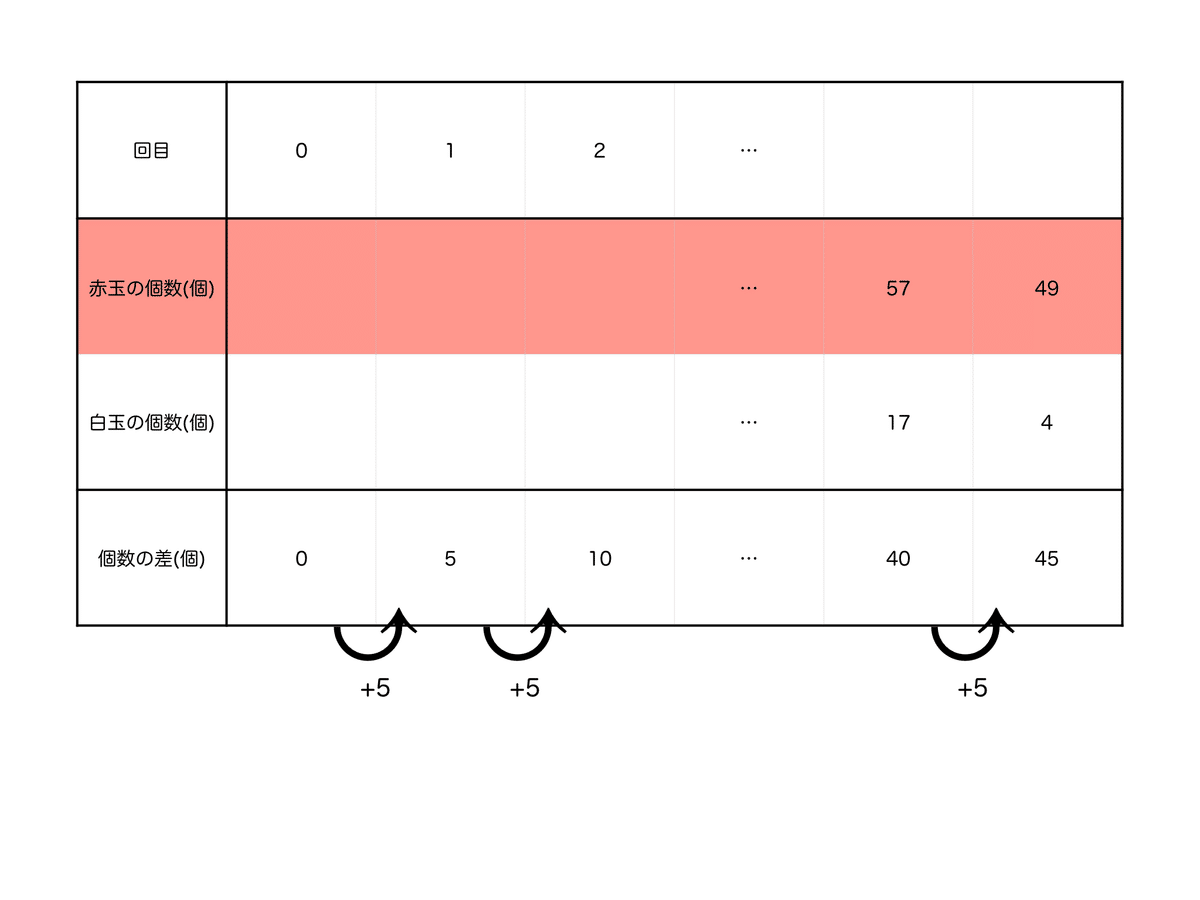
はじめの赤玉と白玉の個数は、8個×9回＋49個＝121個と求められます。
(または13個×9回+4個＝121個と求められます。)

玉を箱に戻して1回に赤玉9個、白玉11個を同時に取り出していくと、白玉がなくなるのは121個÷11個＝11回取り出したときです。

箱の中に残っている赤玉と白玉の個数の差は2個ずつ開いていくので、このときの赤玉の個数は2個×11回で求められます。

$${\fbox{4}}$$

2科目ずつの平均点から合計点を求めます。
国語と算数の2科目の合計点は70点×2＝140点、算数と理科の2科目の合計点は79点×2＝158点、国語と理科の2科目の合計点は76点×2＝152点です。

これらを足し合わせると、国語と算数と理科の3科目の合計点の2倍が450点なので、国語と算数と理科の3科目の合計点は450÷2＝225点です。

(1)算数の得点は、「国語と算数と理科の3科目の合計点」から「国語と理科の2科目の合計点」を引くことで求められます。

(2)国語と算数と理科の3科目の平均点は225点÷3＝75点です。社会の得点はこの92％なので、75点×&&{\tfrac{92}{100}}&&で求められます。

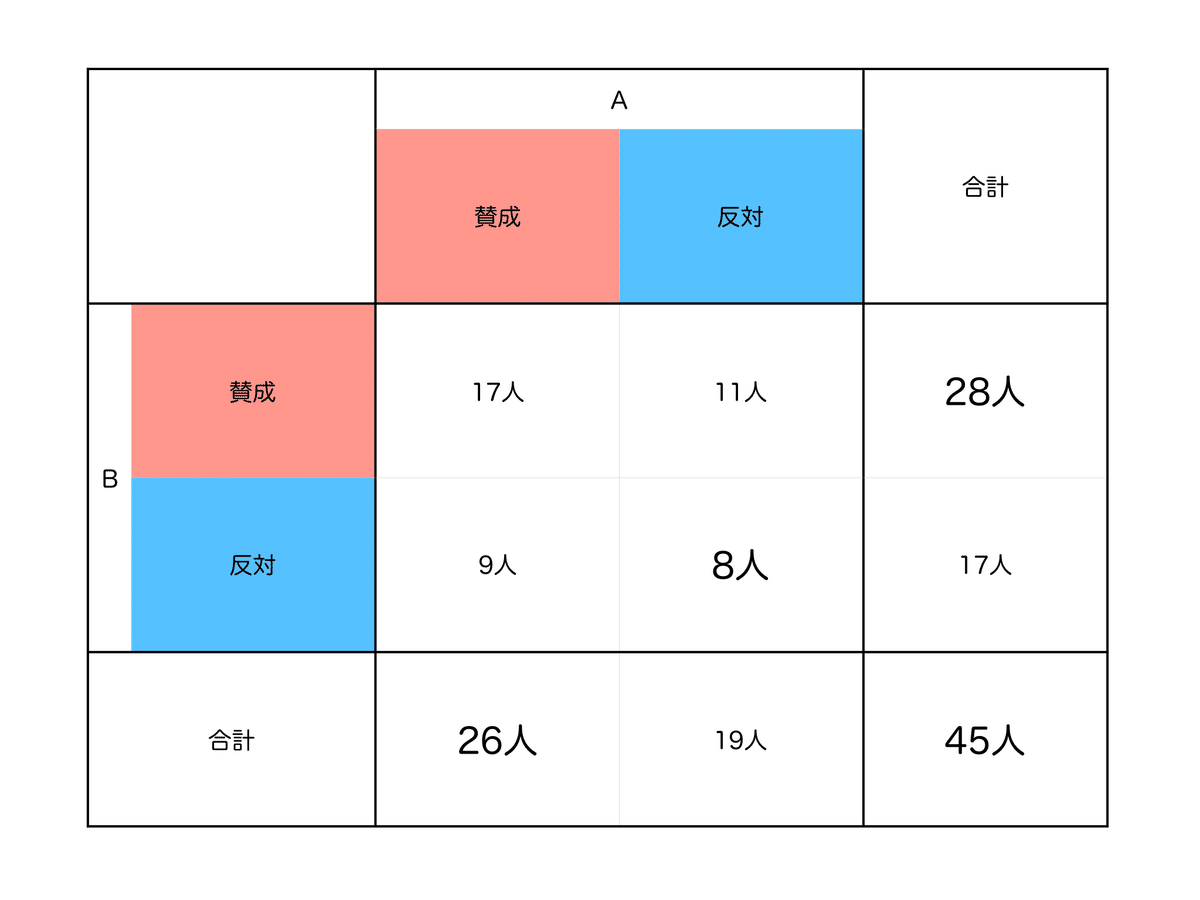
$${\fbox{5}}$$2つの条件を整理

問題文の条件を表に整理します。

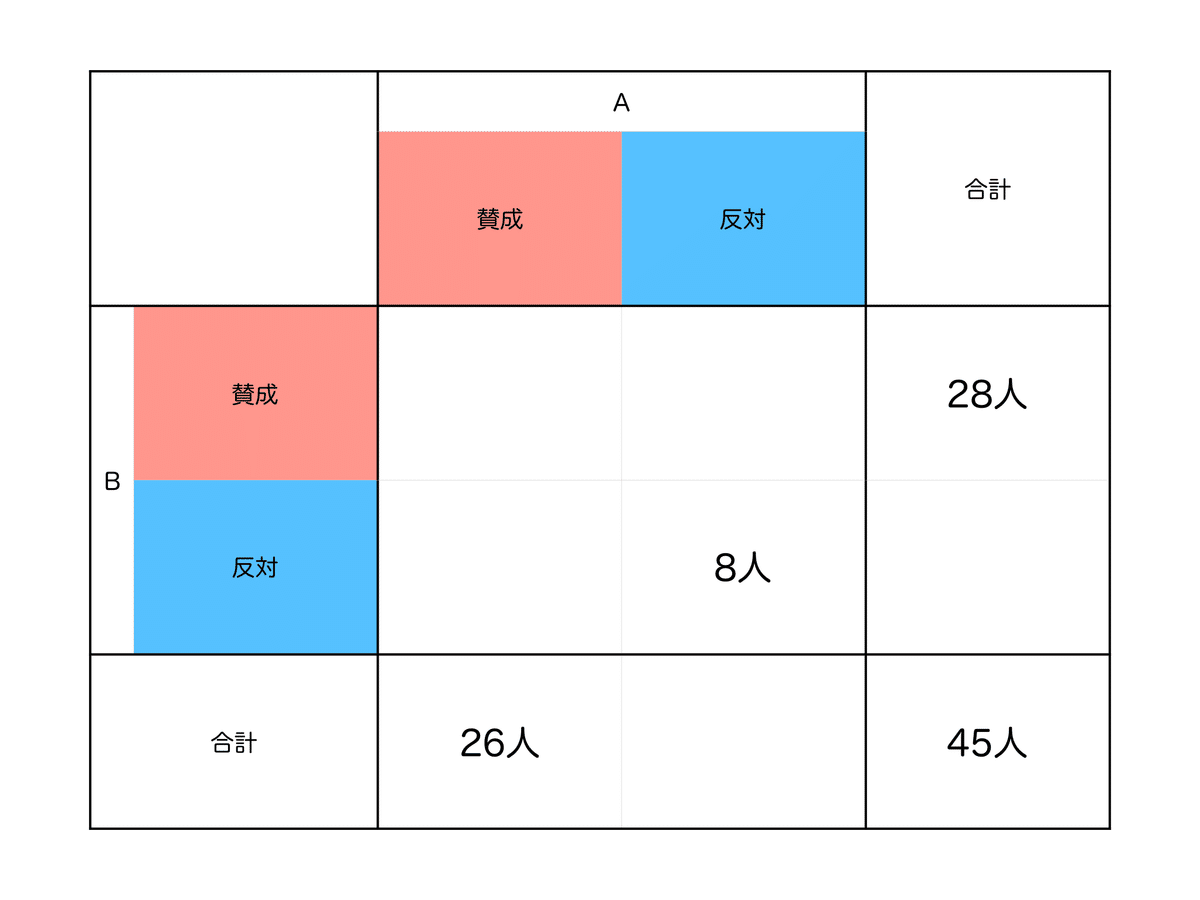
表の空いている部分を埋めると、以下のようになります。

★実践編B以降は有料(500円)でご覧いただけます。