算数6年サピックス　サマーサポート解説［N61-01数の性質］

今回は数の性質の中でも、約数・倍数に関する問題がメインで登場します。

既約分数、星型多角形、全部にぬるための条件は一見違う問題に思えますが、ポイントは共通しています。

★解説を読んでも分からない、授業中に板書を写せないお子様に。テキスト付属の解説はとても簡易的です。そこで家庭学習でお子様が取り組まれるデイリーサポート［実践編A〜E］について、お子様が1人で取り組めるような補助教材を作成しました。

・確認編全問対応
・豊富なカラー図表
・計算の過程も分かる

★著作権の関係で問題文そのものは掲載しておりません。万一誤字脱字、ご要望などございましたらコメント欄にお願いいたします。対応教材は順次増やしていく予定です。

---

今回学ぶこと

• アプローチ$${\textcircled{\small{1}}}$$数の性質(基本)→A$${\fbox{1}}$$

• アプローチ$${\textcircled{\small{2}}}$$既約分数の個数(1)→A$${\fbox{2}}$$、既約分数の個数(2)→A$${\fbox{2}}$$、E$${\fbox{3}}$$

• アプローチ$${\textcircled{\small{3}}}$$たすと割り切れる→C$${\fbox{3}}$$、どんな数→C$${\fbox{4}}$$

• アプローチ$${\textcircled{\small{4}}}$$商と余りが等しい→A$${\fbox{4}}$$、2数の和を考える→D $${\fbox{2}}$$

• アプローチ$${\textcircled{\small{5}}}$$同時に聞こえる→B$${\fbox{4}}$$

• アプローチ$${\textcircled{\small{6}}}$$星型多角形(1)→D$${\fbox{4}}$$、星型多角形(2)→D$${\fbox{4}}$$

• アプローチ$${\textcircled{\small{7}}}$$円の中の反射→C$${\fbox{2}}$$、全部にぬるための条件→D$${\fbox{4}}$$

• アプローチ$${\textcircled{\small{8}}}$$同時に発光する→D$${\fbox{3}}$$

復習テキスト

• 41B-11約数、41B-12倍数、41B-16分数の基本、N41-03約数、N41-04倍数、N41-07分数、41B-23分数、F41-02数のせいしつ

• 510-03約数、510-04倍数、510-06分数と小数、H51-01数の性質、N51-01約数・倍数、F51-01数に関する問題

• 61-01数の性質、61-08小数・分数、61-21数の性質

実践編A

$${\fbox{1}}$$数の性質(1)

(1)

・200から600までにある倍数の個数の求め方
　(1から600までにある倍数の個数)−(1から199までにある倍数の個数)

200から600までに、600ー199＝401個の数があります。

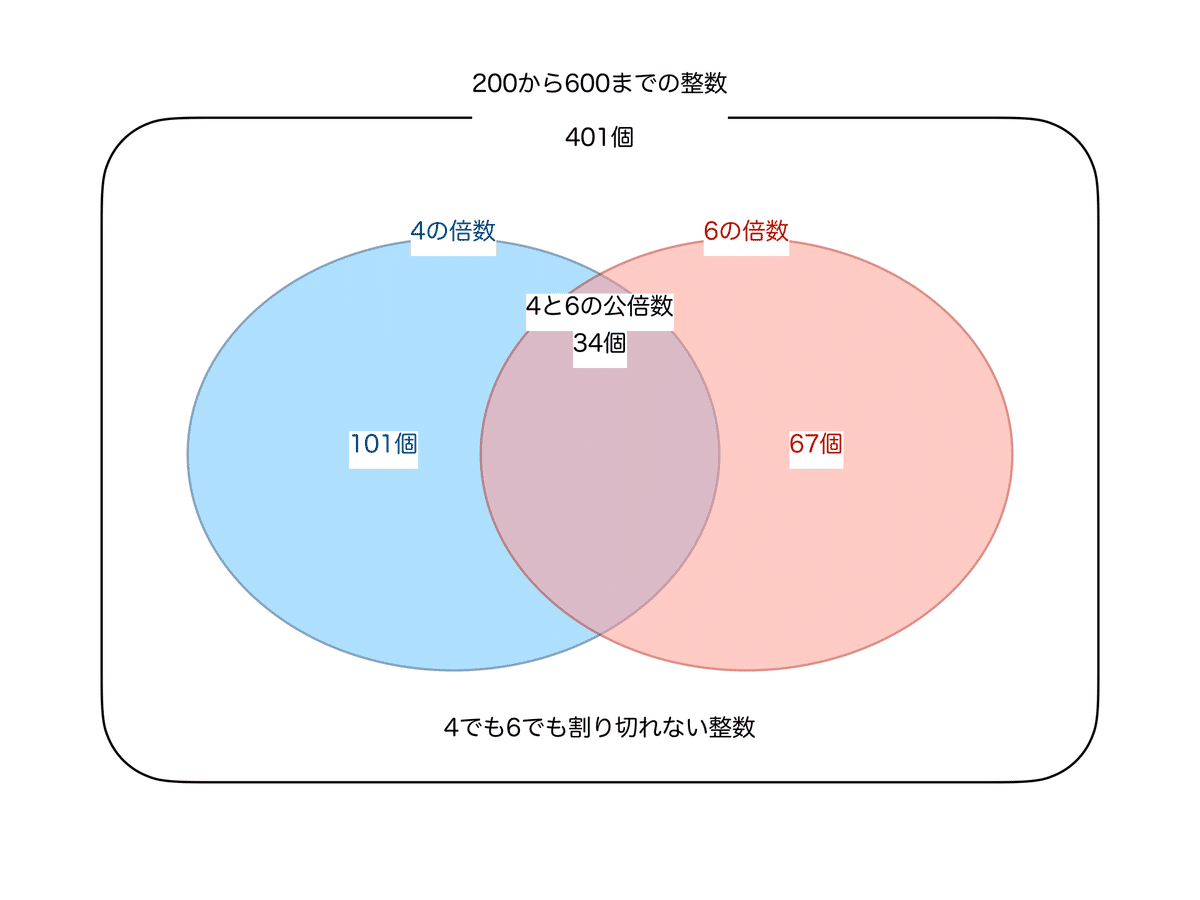
このうち、

4の倍数は、1から600までに600÷4＝150個、1から199までに199÷4＝49個あるので、200から600までには150個−49個＝101個あります。

6の倍数は、1から600までに600÷6＝100個、1から199までに199÷6＝33個あるので、200から600までには100個−33個＝67個あります。

4と6の公倍数(つまり12の倍数)は、1から600までに600÷12＝50個、1から199までに199÷12＝16個あるので、200から600までには50個−16個＝34個あります。

よって、4または6で割り切れる数は101個+67個−34個＝133個あります。

(2)「18で割っても30で割っても4余る」ということは、「18と30の公倍数より4大きい数」です。「3けたの最小の整数」とあるので、18と30の公倍数(つまり90の倍数)より4大きい数のうち、3けたの最小の整数を探しましょう。

(3)「9で割ると2余り、15で割ると8余る」ということは、もし7大きければ「9で割っても15で割っても割り切れる」はずです。9と15の公倍数(つまり45の倍数)より7小さい数のうち、3けたの最大の整数を探しましょう。

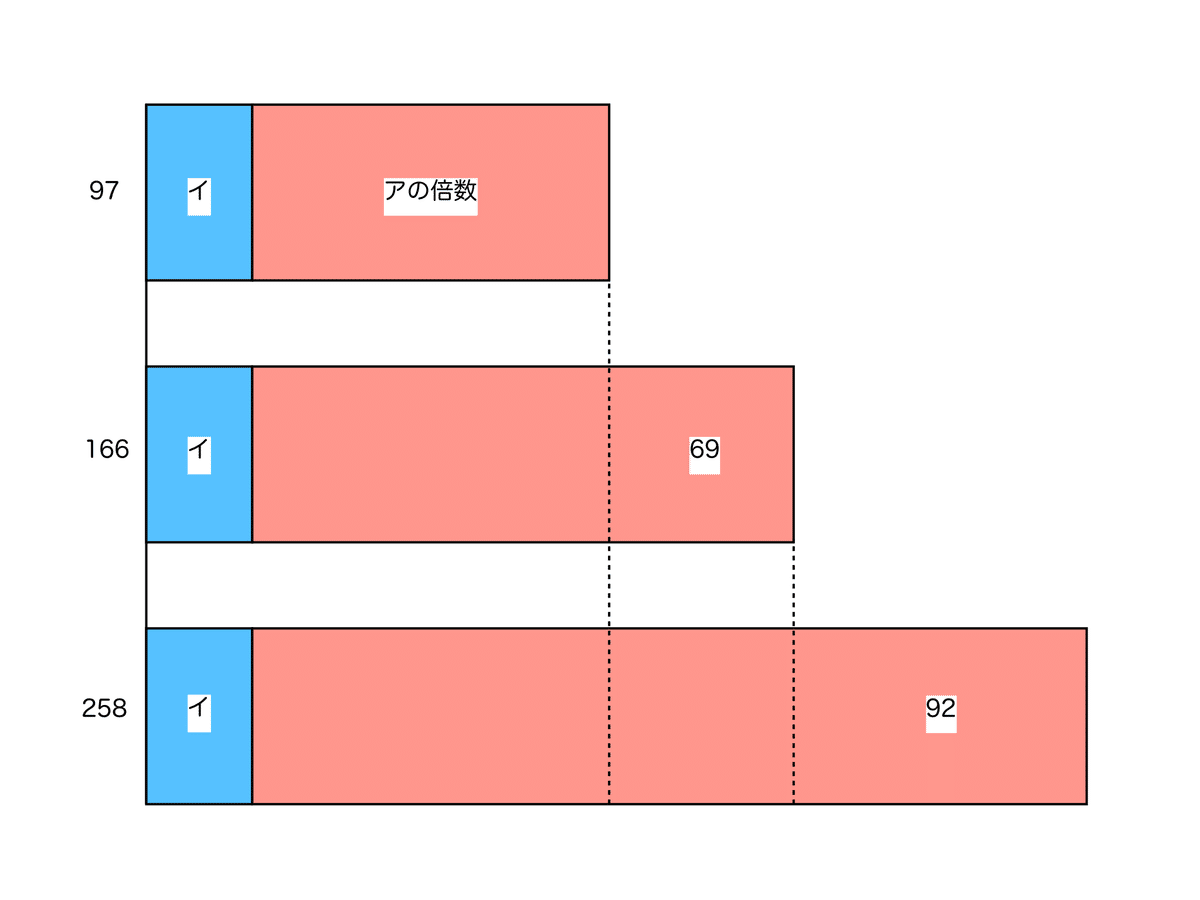
(4)97,166,258から余りのイを引いた数は、いずれもアの倍数です。差に注目すると、97と166の差の69、166と258の差の92もアの倍数と分かります。

$${\fbox{2}}$$どんな数

ある数に4を加えると7の倍数になるということは、「7で割ると3余る」数です。ある数から3を引くと10の倍数になるということは、「10で割ると3余る」数です。

「7で割っても10で割っても3余る」ということは、もし3小さければ「7で割っても10で割っても割り切れる」はずです。7と10の公倍数(つまり70の倍数)より3大きい数を探しましょう。

$${\fbox{3}}$$既約分数の個数(1)

(1)分子を30にそろえると、$${\tfrac{2}{3}}$$＝$${\tfrac{30}{45}}$$、$${\tfrac{5}{6}}$$＝$${\tfrac{30}{36}}$$です。

$${\tfrac{30}{45}}$$＜$${\tfrac{30}{\square}}$$＜$${\tfrac{30}{36}}$$となる⬜︎を探します。

素因数分解すると30＝2×3×5なので、$${\tfrac{30}{\square}}$$が既約分数になるのは、⬜︎が2の倍数でも3の倍数でも5の倍数でもないときです。

37から44までで、2の倍数でも3の倍数でも5の倍数でもない整数を探します。
高々8個なので、書き出して調べます。

$${\fbox{4}}$$

(1)b+c＝86、c+d＝90の差に注目します。

(2)(1)と同じように考えて、aとdの和とcとdの和を比べます。

a+b+c+d＝137、b+c＝86なので、a+d＝137−86＝51です。
a+d＝51、c+d＝90の差に注目します。

(3)和差算に持ち込むにはまだ条件が足りません。
「dはbより4大きいこと」「a,b,c,dはすべて異なる数で、小さい順であること」から、もう少し条件を絞ります。

cとdの和が90と分かっているので、cとdの差が分かれば和差算で求めることができます。cとdの差は1,2,3のいずれかです。

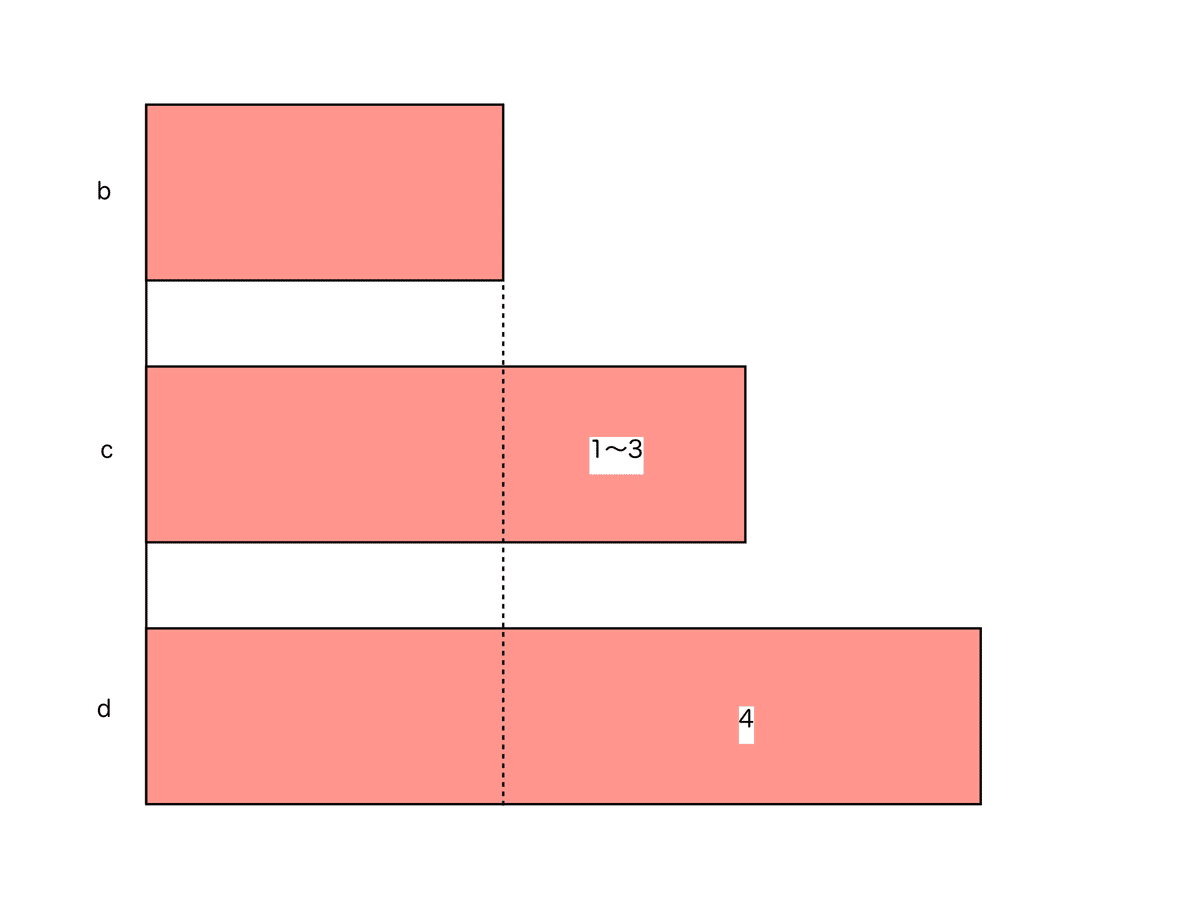
cとdの和は90で偶数ですが、和が偶数になるのは(偶数)+(偶数)もしくは(奇数)+(奇数)のときなので、cとdの差は必ず偶数です。

よってcとdの差は2なので、和差算でc,dを求めることができます。

★実践編B以降は有料(500円)でご覧いただけます。