2023年 武蔵中 算数分析
設問分析
今年は珍しく、速さの出題がありませんでした。受験者平均点は52.9点、合格者平均点は70.5点と差がかなり大きくついています。その要因も合わせてお話していきます。
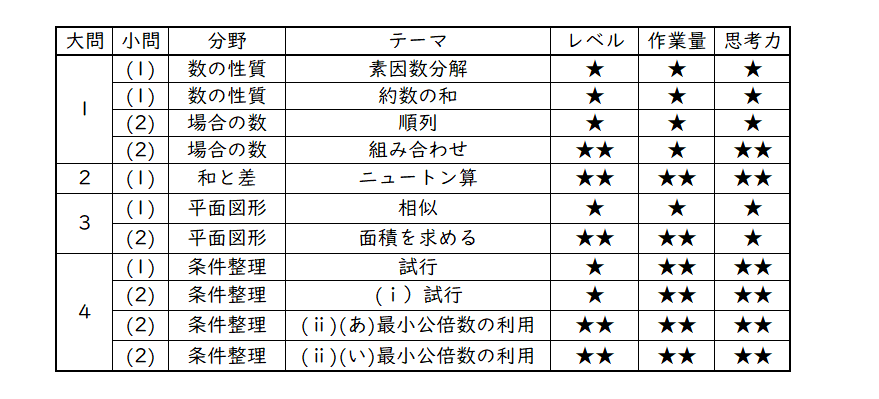
大問1 数の性質 場合の数
(1)は約数の個数が6個しかないので、問題なく正解できたでしょう。
(2)は1つ目は易しいものの、2つ目はかなり大変です。★3にしようかと思いましたが、書き出して正解できる範囲なので★2にしておきました。本番の正答率も低かったのではないかと思います。
つまり、大問1ではあまり差がつきません。
大問2 文章題
「ニュートン算」と書きましたが、題材こそ「ニュートン算」なものの、どちらかというと「つるかめ算」に分類してもよいものでした。難易度はそこまで高くありませんが、あまり見かけないタイプの問題であったため、苦労した受験生も多かったかもしれません。しかし、この問題で確実に差がついたなと予想しています。
大問3 平面図形
(1)は相似を用いて簡単に答えが出せます。(2)は差がつきます。斜線部分の面積を求める方針をたて(引き算で解く生徒が多かったはず)、それを実行するのにどの部分の長さが必要なのかを考えながら進めていくという、ややレベルの高い問題でした。数値も複雑です。算数が得意な受験生とそうでない受験生で一番差がつく問題です。
大問4 条件整理
武蔵の十八番、調べの問題です。本問は意味を理解するのには苦労しませんが、どのような法則が隠れているかを見つけるのに苦労します。問われている数が大きくはないため、丁寧に調べあげられれば半分以上のマルはついたと考えられます。ここでも比較的差はつきやすいでしょう。
全体を通して、時間配分も大切ですが、失敗してしまう受験生はどの問題も中途半端になりがちです。解くべき問題(武蔵中の受験生ならば平面図形と調べは徹底的に準備してきたはず)をミスなく得点したいですね。
武蔵中合格のために
武蔵中の受験生は「速さ」「平面図形」「条件整理」を徹底的にトレーニングします。本年もその質で合否が決まったことでしょう。一方で、大問1や大問2でも細かい差はつきます。本年に共通していえたのは、計算力も大切であるということです。大問1~3は計算までしっかり行えないと答えが出せない問題ばかりでした。方針はあっていたが、計算で間違えたため得点が伸ばせなかった受験生もいたでしょう。
また、武蔵中の入試では、途中式や考え方も書かなければなりません。ある程度テンポよく、そして自分や採点者が途中経過を見ることが出来るように普段から記す習慣をつけましょう。模範解答のように綺麗に書く必要はありません。あくまで先に進むために必要なメモで構いませんので、普段の学習から意識してみてください。
とはいえ、本格的なトレーニングは早くて小6の夏休みからでよいでしょう。特別な解法技術や難問トレーニングが必要な学校ではありませんので、基本~標準的な問題をミスなく解ける状態に訓練しておきましょう。