
二十五、遠近法的な描画。四角錘型の視体積を作成する。(WebGL)
■サンプルページはコチラ↓
■このプログラムの解説は、次のExcelファイルをご覧下さい。
.oOo..oOo..oOo.
↓ HTMLのコードです。
<!DOCTYPE html>
<html lang="ja">
<head>
<meta charset="utf-8" />
<title>視体積を設定する(四角錐型)</title>
</head>
<body onload="main()">
<canvas id="webgl" width="400" height="400">
Canvasをサポートしているブラウザを使用してください。
</canvas>
<p>キーボードの矢印キーを使って視点を左右に移動できます。</p>
<ul>
<li>右矢印キー: 視点を右に移動</li>
<li>左矢印キー: 視点を左に移動</li>
</ul>
<script src="webgl-utils.js"></script>
<script src="webgl-debug.js"></script>
<script src="sano-func.js"></script>
<script src="gyouretsu-7-4.js"></script>
<script src="PerspectiveView2.js"></script>
</body>
</html>.oOo..oOo..oOo.
↓ JavaScriptのコードです。
//今回の。
// 頂点シェーダのプログラム
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'attribute vec4 a_Color;\n' +
'uniform mat4 u_ViewMatrix;\n' +
'uniform mat4 u_ProjMatrix;\n' +
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_Position = u_ProjMatrix * u_ViewMatrix * a_Position;\n' +
' v_Color = a_Color;\n' +
'}\n';
// フラグメントシェーダのプログラム
var FSHADER_SOURCE =
'#ifdef GL_ES\n' +
'precision mediump float;\n' +
'#endif\n' +
'varying vec4 v_Color;\n' +
'void main() {\n' +
' gl_FragColor = v_Color;\n' +
'}\n';
function main() {
// Canvas要素を取得する
var canvas = document.getElementById('webgl');
// WebGL描画用のコンテキストを取得する
var gl = getWebGLContext(canvas);
if (!gl) {
console.log('WebGLコンテキストの取得に失敗');
return;
}
// シェーダを初期化する
if (!initShaders2(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
console.log('シェーダの初期化に失敗');
return;
}
// 頂点座標と色を設定する(青い三角形が手前にある)
var n = initVertexBuffers(gl);
if (n < 0) {
console.log('頂点情報の設定に失敗');
return;
}
// Canvasをクリアする色を設定する
gl.clearColor(0, 0, 0, 1);
// u_ViewMatrixとu_ProjMatrix変数の格納場所を取得する
var u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix');
var u_ProjMatrix = gl.getUniformLocation(gl.program, 'u_ProjMatrix');
if (!u_ViewMatrix || !u_ProjMatrix) {
console.log('u_ViewMatrixかu_ProjMatrixの格納場所の取得に失敗');
return;
}
var viewMatrix = new Matrix4(); // ビュー行列
// var projMatrix = new Matrix4(); // 投影行列
// キーが押された場合のイベントハンドラを設定する
window.onkeydown = function(ev){ keydown(ev, gl, n, u_ViewMatrix, viewMatrix); };
// 視体積を指定するための行列(平行投影行列)を作成しu_ProjMatrixに設定する
var projMatrix = new Matrix4();
projMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
// projMatrix.setOrtho(-1.0, 1.0, -1.0, 1.0, 0.0, 2.0);
gl.uniformMatrix4fv(u_ProjMatrix, false, projMatrix.elements);
draw(gl, n, u_ViewMatrix, viewMatrix); // 描画する
}
function initVertexBuffers(gl) {
var verticesColors = new Float32Array([
// 右側の図形3つ。頂点座標、色
0.59, -0.26, -4.0, 0.1, 0.1, 0.3, //一番奥。ハンブラビみたいな色の図形。
1.0, 0.67, -4.0, 0.3, 0.5, 0.9,
1.0, 0.0, -4.0, 0.1, 0.1, 0.3,
1.41, -0.26, -4.0, 0.1, 0.1, 0.3,
1.0, 0.67, -4.0, 0.3, 0.5, 0.9,
1.0, 0.0, -4.0, 0.1, 0.1, 0.3,
0.59, -0.26, -2.0, 0.6, 0.9, 0.7, //真ん中。クィン・マンサみたいな色の図形。
1.0, 0.67, -2.0, 0.8, 0.7, 0.5,
1.0, 0.0, -2.0, 0.6, 0.9, 0.7,
1.41, -0.26, -2.0, 0.6, 0.9, 0.7,
1.0, 0.67, -2.0, 0.8, 0.7, 0.5,
1.0, 0.0, -2.0, 0.6, 0.9, 0.7,
0.59, -0.26, 0.0, 0.4, 0.2, 0.3, // 一番前。シーマ専用機みたいな色の図形。
1.0, 0.67, 0.0, 0.9, 0.9, 0.5,
1.0, 0.0, 0.0, 0.4, 0.2, 0.3,
1.41, -0.26, 0.0, 0.4, 0.2, 0.3,
1.0, 0.67, 0.0, 0.9, 0.9, 0.5,
1.0, 0.0, 0.0, 0.4, 0.2, 0.3,
// 左側の図形3つ。頂点座標、色
-1.41, -0.26, -4.0, 0.1, 0.1, 0.3, //一番奥。ハンブラビみたいな色の図形。
-1.0, 0.67, -4.0, 0.3, 0.5, 0.9,
-1.0, 0.0, -4.0, 0.1, 0.1, 0.3,
-0.59, -0.26, -4.0, 0.1, 0.1, 0.3,
-1.0, 0.67, -4.0, 0.3, 0.5, 0.9,
-1.0, 0.0, -4.0, 0.1, 0.1, 0.3,
-1.41, -0.26, -2.0, 0.6, 0.9, 0.7, //真ん中。クィン・マンサみたいな色の図形。
-1.0, 0.67, -2.0, 0.8, 0.7, 0.5,
-1.0, 0.0, -2.0, 0.6, 0.9, 0.7,
-0.59, -0.26, -2.0, 0.6, 0.9, 0.7,
-1.0, 0.67, -2.0, 0.8, 0.7, 0.5,
-1.0, 0.0, -2.0, 0.6, 0.9, 0.7,
-1.41, -0.26, 0.0, 0.4, 0.2, 0.3, // 一番前。シーマ専用機みたいな色の図形。
-1.0, 0.67, 0.0, 0.9, 0.9, 0.5,
-1.0, 0.0, 0.0, 0.4, 0.2, 0.3,
-0.59, -0.26, 0.0, 0.4, 0.2, 0.3,
-1.0, 0.67, 0.0, 0.9, 0.9, 0.5,
-1.0, 0.0, 0.0, 0.4, 0.2, 0.3,
]);
var n = 36;
// バッファオブジェクトを作成する
var vertexColorbuffer = gl.createBuffer();
if (!vertexColorbuffer) {
console.log('バッファオブジェクトの作成に失敗');
return -1;
}
// 頂点の座標と色をバッファオブジェクトに書き込む
gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);
gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);
var FSIZE = verticesColors.BYTES_PER_ELEMENT;
// a_Positionにバッファオブジェクトを割り当て、有効化する
var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
if(a_Position < 0) {
console.log('a_Positionの格納場所の取得に失敗');
return -1;
}
gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
gl.enableVertexAttribArray(a_Position);
// a_Colorにバッファオブジェクトを割り当て、有効化する
var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
if(a_Color < 0) {
console.log('a_Colorの格納場所の取得に失敗');
return -1;
}
gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
gl.enableVertexAttribArray(a_Color);
// バッファオブジェクトのバインドを解除する
gl.bindBuffer(gl.ARRAY_BUFFER, null);
return n;
}
var g_EyeX = 0.20, g_EyeY = 0.25, g_EyeZ = 6.0; // 視点の位置
function keydown(ev, gl, n, u_ViewMatrix, viewMatrix) {
if(ev.keyCode == 39) { // 右矢印キーが押された
g_EyeX += 0.01;
} else
if (ev.keyCode == 37) { // 左矢印キーが押された
g_EyeX -= 0.01;
} else { return; } // 余分な描画を行わないようにする
draw(gl, n, u_ViewMatrix, viewMatrix);
}
function draw(gl, n, u_ViewMatrix, viewMatrix) {
// 視点の位置、方向を指定する
viewMatrix.setLookAt(g_EyeX, g_EyeY, g_EyeZ, 0, 0, 0, 0, 1, 0);
// ビュー行列をu_ViewMatrix変数に設定する
gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);
// Canvasをクリアする
gl.clear(gl.COLOR_BUFFER_BIT);
// 三角形を描画する
gl.drawArrays(gl.TRIANGLES, 0, n);
}
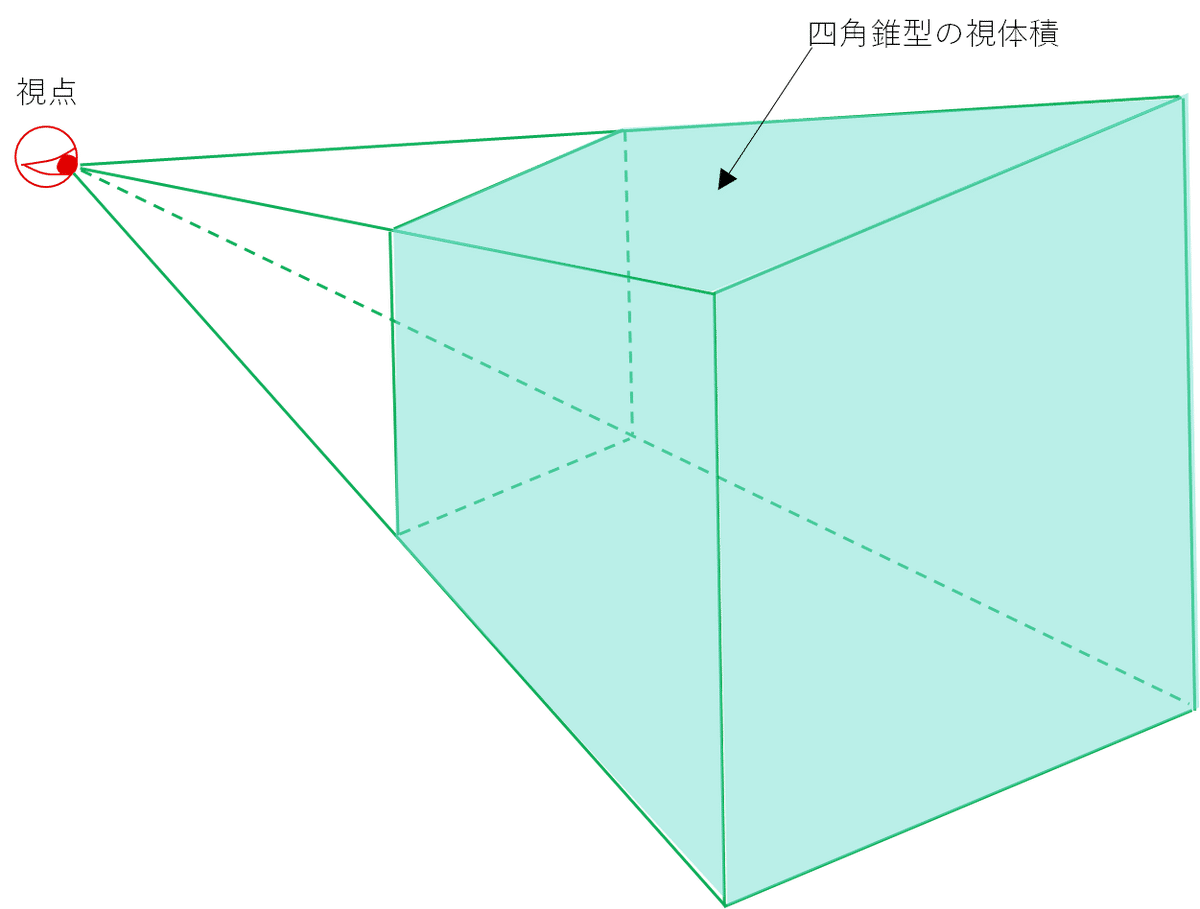

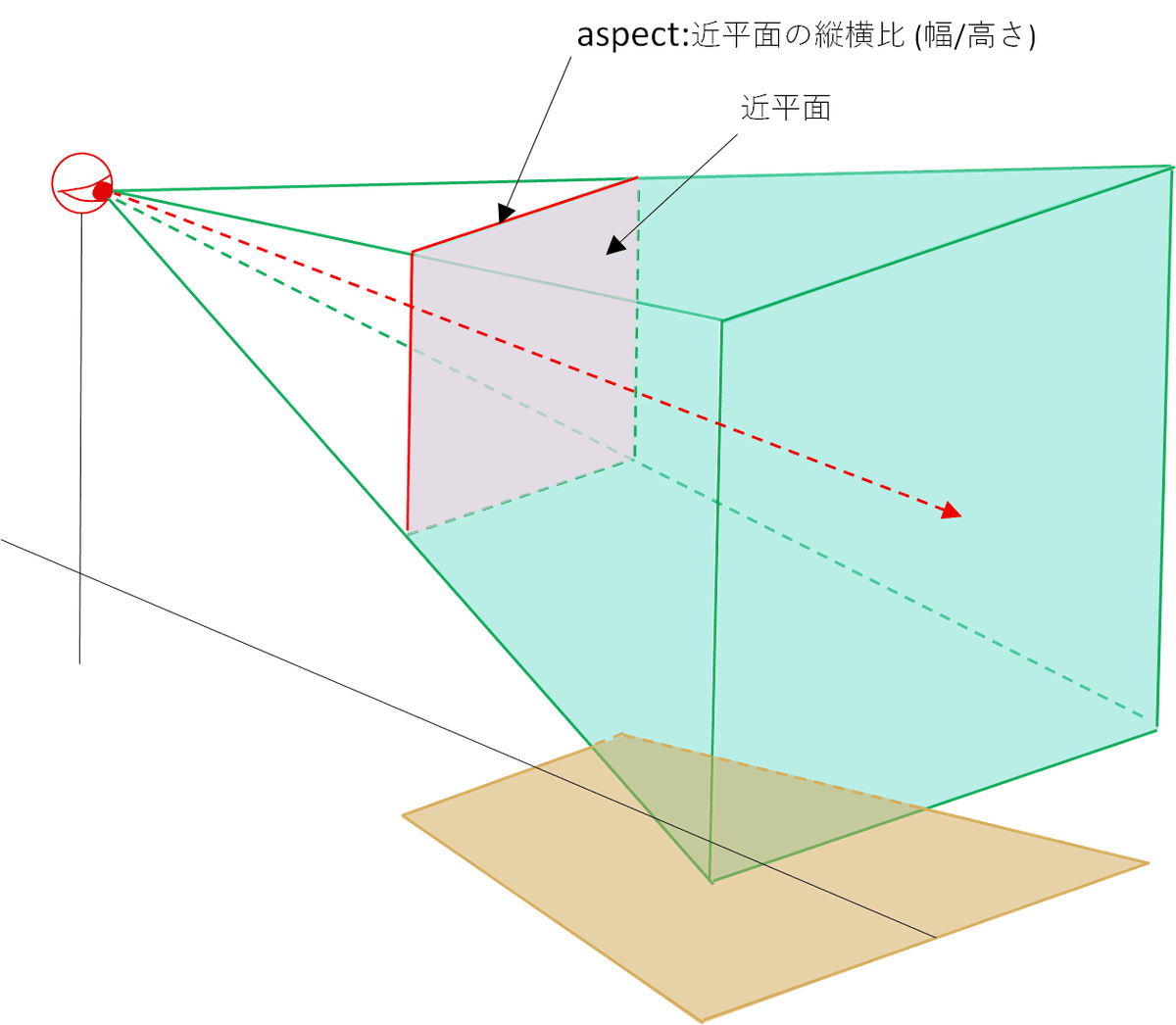

プログラム中に出てくる言葉は上図の様なイメージです。
■参考文献:WebGL+HTML5 3DCGプログラミング入門
(良い本ですが、絶版です。中古で購入される場合はCD-ROMがちゃんと付いているか確認して下さい)
■以下は私が検索する時に使うヤツです。このまま読むと意味が分からないと思います。先程掲載したExcelファイルをご覧下さい。
.oOo..oOo..oOo.
平行投影行列用の変数。 (つまり、視体積用の変数)
乗算の順番は下記のとおりです。
平行投影行列 * ビュー行列 * 頂点座標
WebGLのプログラム内で使用される、uniform変数に対するWebGLのuniform location(一般的にはGPU上のメモリアドレス)を取得しています。
自分の図形 + 書籍の設定 だと、図形が見切れたので調整。
Zの間隔を空けないと遠近感がでないので、大きめに空ける。
.oOo..oOo..oOo.
window → 現在のタブやウィンドウを表すオブジェクト。 (ざっくり)
window.onkeydown → 現在のブラウザのウィンドウがアクティブな状態で、キーが押された場合。
window.onkeydown の右辺は必ず関数にする。
function(ev) は無名関数。ev は変数。 名前は任意だが、e や ev がよく使われる。
keydown は126行目。
window.onkeydown = function(ev){ keydown(ev, gl, n, u_ViewMatrix, viewMatrix); };
1.ウィンドウが開かれた時、(ユーザーはまだキーを操作していない)、”onkeydown” に無名関数が代入されます。
2.ユーザーがキーを押すと、onkeydown イベントが発動します。
3.onkeydown イベントが発動すると、ブラウザは function (ev) を呼び出します。
4.function(ev) の中で、keydown()が実行される。
※JavaScript のイベントリスナーでは、イベントオブジェクト (ev) は自動的にコールバック関数 (無名関数) に渡されるので、return などを使わなくてよい。
※イベントオブジェクト (ev) にはクリックしたときの座標データなどが含まれているらしい。
”gyouretsu”ファイルへ。
シェーダーに行列を送る。
第1引数は、シェーダー内でのuniform変数の場所。(←54行目で設定) 第2引数は、転置するかどうか。第3引数は別途作成した4x4行列の名前。
Matrix4(配列名)と書いた場合、その配列がコピーされる。それ以外は単位行列。
otherには、他の行列が入る。otherは引数の様に使われている。(予約語ではない)
concat → concatenate (連結する) の略と思われる。
かけられる方の行列の要素。elements の中身は15行目から。elementsは任意の名前。
上の行と同じ物を入れているのは、後で計算に使う為。
右からかける方の行列。
こう書くことにより、multiply メソッドは concat メソッドの引数を受け取ることができます。
正射影行列。←パース的でなく、直方体的な感じで3Dオブジェクトを表示。メカCADの絵の様なもの。
2次元のキャンバス上に3次元的な図を、遠近感なしで描く際に使われます。
左クリップ平面のX座標と、右クリップ平面のX座標が同じ値だと、幅がゼロということなので、表示できなくなる。
throw は、JavaScriptで例外を発生させるキーワードです。通常、プログラムの実行中に何らかのエラーが発生した場合に、処理を中断し、エラーメッセージやオブジェクトを外部に伝えるために使われます。
'null frustum' は、著者が決めたエラーメッセージなので、自分の好きなエラーメッセージでOK。
right - left は直方体の幅。 その逆数 (rw) を計算して、直方体を正規化する。
245行目からは、これ↓をやっている。
この部分の数式は、OpenGLなどのCGで使われる行列や数式です。
これらは、特定の描画や視覚化の目的に合わせたものが多く、数学の教科書に出てくる行列(例えば回転行列など)とは異なる側面があります。
数学的にはあまり一般的でないかもしれませんが、CGの世界では標準的で非常に重要なものです。
3Dモデルの座標を、ここで指定した視体積の中に、相対的な位置関係を保ちながら押し込める、そして、2次元のcanvasに投影する、というイメージ
e[0], e[5], e[9] はスケーリング、e[12]~e[14]は平行移動。平行移動させるのは、3Dモデルの中心と、視体積の中心を合わせるため。
throw はエラーや例外を明示的に発生させるための構文です。
コードが特定の条件を満たした場合、例外をスローして、プログラムの通常のフローを中断し、エラーハンドリングが行われるか、プログラムが終了するようにします。
fovy は、”field of view in Y direction” の略と思われる。
sin (fovy) がゼロだとダメな理由。
fovy = 0 deg の場合。Y方向の視野角がゼロなので、何も見えない状態になる為。
fovy = 180 deg の場合。Y方向の視野角が無限に広いということになり、投影行列が無効になる。
rd は reciprocal of distance (距離の逆数) の略と思われる。
ct は cotangent (コタンジェント) の略と思われる。
アスペクト比を保つ。
Y方向のスケーリング。
奥行 (深度) の計算。
遠近法にする為に、本来の座標データをスケーリングしている。 (遠くの物を小さく)
WebGLは-1から1の範囲で描画されるので、-1-1 = -2 という定数が出てくるらしい。 2以外だと表示がおかしくなるらしい。
return this で、オブジェクトそのものを返す。
書籍では、注視点(atX, atY, atZ) と書かれている。
(注視点) - (視点) 。カメラの視点から注視点への方向(ベクトル)を計算している。
つまり、カメラの向き。
rlfはReciprocal of Length of "f" の略だと思われます。Reciprocal は逆数の意味。
カメラの向きとカメラの上方向の外積を計算することにより、カメラの右方向を計算している。
カメラの右方向とカメラの向きの外積を計算し、カメラの上方向を計算している。
upX, upY, upZ はカメラが上を向いている大まかな方向を示すベクトルであり、カメラの座標系における正確な上方向ベクトル(ux, uy, uz)とは必ずしも一致しません。
upX, upY, upZ は、カメラの「初期上方向」を表す目安でしかなく、これがカメラの視線ベクトルや右方向ベクトルと正確に直交する保証はありません。
そのため、視線ベクトル(f)と右方向ベクトル(s)が確定した後、これらと直交する形でカメラの正確な上方向ベクトル(ux, uy, uz)を再計算する必要があります。
fにマイナスをかけるのは、視線ベクトルは通常「負のZ軸」に沿って定義されることが多いためです。
これは、物体が「負のZ軸」方向にあることが多いためです。
後で、3D座標の行列と掛け算するので、カメラの視点を原点に移動させる。
いいなと思ったら応援しよう!

