
OCamlの二分木を可視化するプログラムの作成
はじめに
この記事は、OCaml(関数型プログラミング言語)によるプログラムの作成記事です。作成するプログラムは、二分木を画像に変換するためのものです。
想定する読者は、OCamlのプログラム初心者や、二分木愛好家、可視化マニアなどです。
作成に至る経緯
文字だけの記事は嫌だ
最近、OCamlの練習問題に挑戦する記事を再開しました。今、記事で取り組んでいる題材は、二分木です。
この二分木は、文字通り木なので、文字だけでは全体像を想像することができません$${^※}$$。当然、記事も分かり難くなっています。
できれば、バンバン図を入れてガンガンビュー数を上げたいところです。
ビュー数を考えると、作図プログラムも自作できれば嬉しいのですが、それには能力も時間も全然足りません。
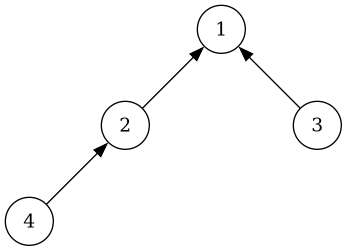
※ 例えば、下図の二分木を文字だけで表現すると、
Node (1, Node (2, Node (4, Empty, Empty), Empty), Node (3, Empty, Empty))
になります。
Graphviz
OCamlの母国フランスには、有名な格言があります。そう「パンがなければケーキを…」です。
それに倣い「自作が無理なら他作を」と言うことで、ネットの海を彷徨い出会ったのが「オープンソースのグラフ可視化ソフトウェア」Graphvizです。
Graphvizは、簡素な文字言語(DOT言語)によるグラフ$${^※}$$の記述から、様々な形式の図を生成することができます。
しかし、残念なことに、OCamlからはGraphvizを直接に使うことはできません。Graphvizを使うには、OCamlのデータを、DOT言語で書かれた記述ファイル(dotファイル)に変換する必要があります。
そこで、その変換プログラムを作りました!と言うのが、本記事の内容です。
※ ここで言うグラフは、所謂グラフ理論のグラフ(頂点と辺からなる)です。また木は、グラフの一種(閉路を持たない連結なグラフ)です。
使用例
プログラムの具体的な説明に入る前に、その機能が理解し易くなるよう、まずは使用の一例を示します。
大まかな流れは、次の通りです。
二分木→[練習問題のプログラム]→
座標付き二分木→[本記事のプログラム]→
dotファイル→[Graphviz]→
画像ファイル
入力データと出力データ
二分木は、OCamlの内部データです。
(* OCamlの二分木 *)
Node ('n',
Node ('k',
Node ('c', Node ('a', Empty, Empty),
Node ('h', Node ('g', Node ('e', Empty, Empty), Empty), Empty)),
Node ('m', Empty, Empty)),
Node ('u', Node ('p', Empty, Node ('s', Node ('q', Empty, Empty), Empty)),
Empty))座標付き二分木も、OCamlの内部データです。このデータは、練習問題の答案(プログラム)により生成されます。
(* 座標付き二分木 *)
Node (('n', 7, 0),
Node (('k', 5, 1),
Node (('c', 1, 2), Node (('a', 0, 3), Empty, Empty),
Node (('h', 4, 3),
Node (('g', 3, 4), Node (('e', 2, 5), Empty, Empty), Empty), Empty)),
Node (('m', 6, 2), Empty, Empty)),
Node (('u', 11, 1),
Node (('p', 8, 2), Empty,
Node (('s', 10, 3), Node (('q', 9, 4), Empty, Empty), Empty)),
Empty)) dotファイルは、DOT言語によりグラフの構造を記述したものです。
このdotファイルを生成するのが本記事のプログラムです。
// DOT言語のファイル
digraph 1 {
node [shape = circle];
splines = false;
n [pos = "8, 6!"];
k [pos = "6, 5!"];
c [pos = "2, 4!"];
a [pos = "1, 3!"];
h [pos = "5, 3!"];
g [pos = "4, 2!"];
e [pos = "3, 1!"];
m [pos = "7, 4!"];
u [pos = "12, 5!"];
p [pos = "9, 4!"];
s [pos = "11, 3!"];
q [pos = "10, 2!"];
k -> n
c -> k
a -> c
h -> c
g -> h
e -> g
m -> k
u -> n
p -> u
s -> p
q -> s
}本記事の画像ファイルは、pngファイルです。Graphvizの「dotコマンド」により生成されます。

プログラムの構成と説明
二分木のモジュール
module Binary_tree : (sig
(* 二分木の型定義 *)
type 'a t = Empty | Node of 'a*'a t*'a t
(* 二分木の高さを求める関数 *)
val height_of : 'a t -> int
end)
= struct
type 'a t = Empty | Node of 'a*'a t*'a t
let rec height_of = function
Empty -> 0 | Node (_, l, r) -> 1+max (height_of l) (height_of r)
end コメントにもあるように、型と高さ関数を定義しています。
dotファイルへの変換関数
open Binary_tree
let dot n tr =
let tab = " " in
let h = height_of tr in
print_string "digraph ";
print_int n;
print_endline " {";
print_string tab;
print_endline "node [shape = circle];";
print_string tab;
print_endline "splines = false;";
let rec print_node = function
| Empty -> ()
| Node ((a, x, y), l, r) ->
print_string tab;
print_char a;
print_string " [pos = \"";
print_int x;
print_string ", ";
(* y座標の変換 *)
print_int (h-y-1);
print_endline "!\"];";
print_node l;
print_node r in
let rec print_edge =
let print_arrow p = function
| Empty -> ()
| Node ((c, _, _), _, _) as n ->
print_string tab;
print_char c;
print_string " -> ";
print_char p;
print_newline ();
print_edge n in
function
| Empty -> ()
| Node ((a, _, _), l, r) ->
print_arrow a l;
print_arrow a r in
print_node tr;
print_edge tr;
print_endline "}"; 長いですが、ほとんどはprint文です(本体は10行ちょっとです)。
注意すべき点は、二分木とdotファイルとでy座標が逆になっているので、それらを変換しているところです。
int型の二分木をchar型の二分木に変換する関数
open Binary_tree
let rec to_ctree = function
| Empty -> Empty
| Node (i, l, r) -> Node (char_of_int (i+48), to_ctree l, to_ctree r)私自身は、int型の二分木を使って問題を解いているのですが、問題文ではchar型の二分木が使われることが多いので、前者を後者に変換する関数を用意しました。
どの関数も極めて単純なので、ソースコードとコメントだけで十分に理解できると思います。
まとめ
大袈裟にごちゃごちゃと書きましたが、所詮は文字列をちょこっと変換するだけのちゃちなプログラムです。
むしろプログラムなんかよりも、OCamlのモジュール化やDOT言語の理解のほうが、ずっと苦労しました。
ならば、そちらを題材にするべきなのですが、必要最低限の知識をペロッと舐めた程度なので、理解が薄く、とても記事にできたものではありません。
まあ、noteなので、技術的な内容は求められてないでしょう。それよりも、もっとフワフワとした意識の高い妄言や、内容の薄い繰り言を書いたほうが、note読者には受けが良かったかなと思います。でも苦手なんですよね、こんな風にグダグダと何を主張したいのか分からないけど分量だけは多い駄文が。
それでは、このようなゴミでも、ここまでお付き合い戴いた方の一助となれば、これ幸です。
いいなと思ったら応援しよう!

