切稜立方体の隣接する２面角は120°と135°

135°の方は45°で切り落とすので、90°+45°で135°になるのは小学生に聞かなくとも分かります。120°は六角形で配置するために必須の角度で、三角山パズルの基本となります。しかし、直角だらけの立方体から120°が生じるのはどういうことなのでしょう。しばらく考え込まないと、いいえ、鉛筆で絵を描いてみないと分からないかもしれません。

内接球を持つ切稜立方体

中学受験の勉強サイトで立方体を切断が取り上げられています。小学生はこんなことも考えているのかと驚きました。

立体図形を切断したがる中学入試問題

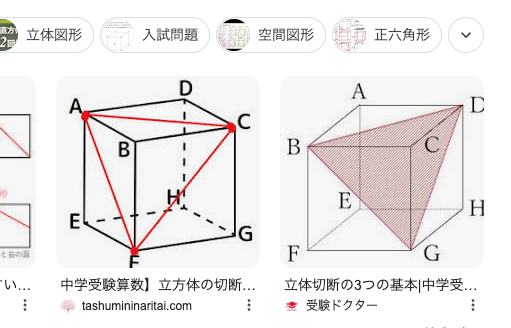
上の図の左側の立方体の記号を使うと、点A、点C、点Fを結んだ三角形は正三角形です。辺の長さが等しいので図形を見れば計算する必要もありません。

立方体の隣り合う辺の中点と中心を結ぶ三角形は、立方体を8個の小さな立方体に分割して考えた時に「中学入試問題」と同じ状況になっていて、正三角形です。切稜面は辺の中点と中心を結ぶ直線に垂直ですから、正三角形の面は二つの切稜面と垂直に交わる面となります。正三角形の面に切稜面の交線を2本書くと120°で交わりますので、切稜面同士は120°になるということです。

立方体の切稜面同士は120°で交わる

赤い面は正三角形、緑の二面の角度は120°

3Dモデル（中心方向）

3Dモデル（斜めから）

いつか、中学受験の問題に切稜立方体が出ることもあるのかな。