漸化式 基本の3パターンの一般項

漸化式とは？

ある項をそれ以前の項を用いて表す。

$$
ある項とは次でいうa_{n+1}のこと
$$

基本の3パターン

$$
a_{n+1} = a_n + d… (等差数列)
$$

$$
a_{n+1} = ra_n…(等比数列)
$$

$$
a_{n+1}=a_n+f(n)…(階差数列)
$$

1.等差数列

$$
a_n = a + (n-1)d…(等差数列の一般項)
$$

どうしてこうなるのか…
1つずつ見ていきましょう。

$$
a_1=a
$$

$$
a_2=a+d
$$

$$
a_3=a+2d
$$

$$
a_4=a+3d
$$

$$
…
$$

$$
a_n = a + (n-1)d
$$

2.等比数列

$$
a_n=ar^{n-1}(等比数列の一般項)
$$

等差数列と同様に

$$
a_1 = a
$$

$$
a_2=ar
$$

$$
a_3=ar^2
$$

$$
a_4=ar^3
$$

$$
…
$$

$$
a_n=ar^{n-1}
$$

3.階差数列

$$
n≧2の時        a_n=a_1+\sum_{k=1}^{n-1} b_k
$$

$$
数列b_nの初項から第(n-1)項までをまとめて\sum_{k=1}^{n-1}b_k
となります。
$$

k=1は初項のことを指しています。

$$
※n≦1の時は\sum_{k=1}^{n-1}b_kの答えが不確定
$$

なので、n≧2となります。
最後に証明です。

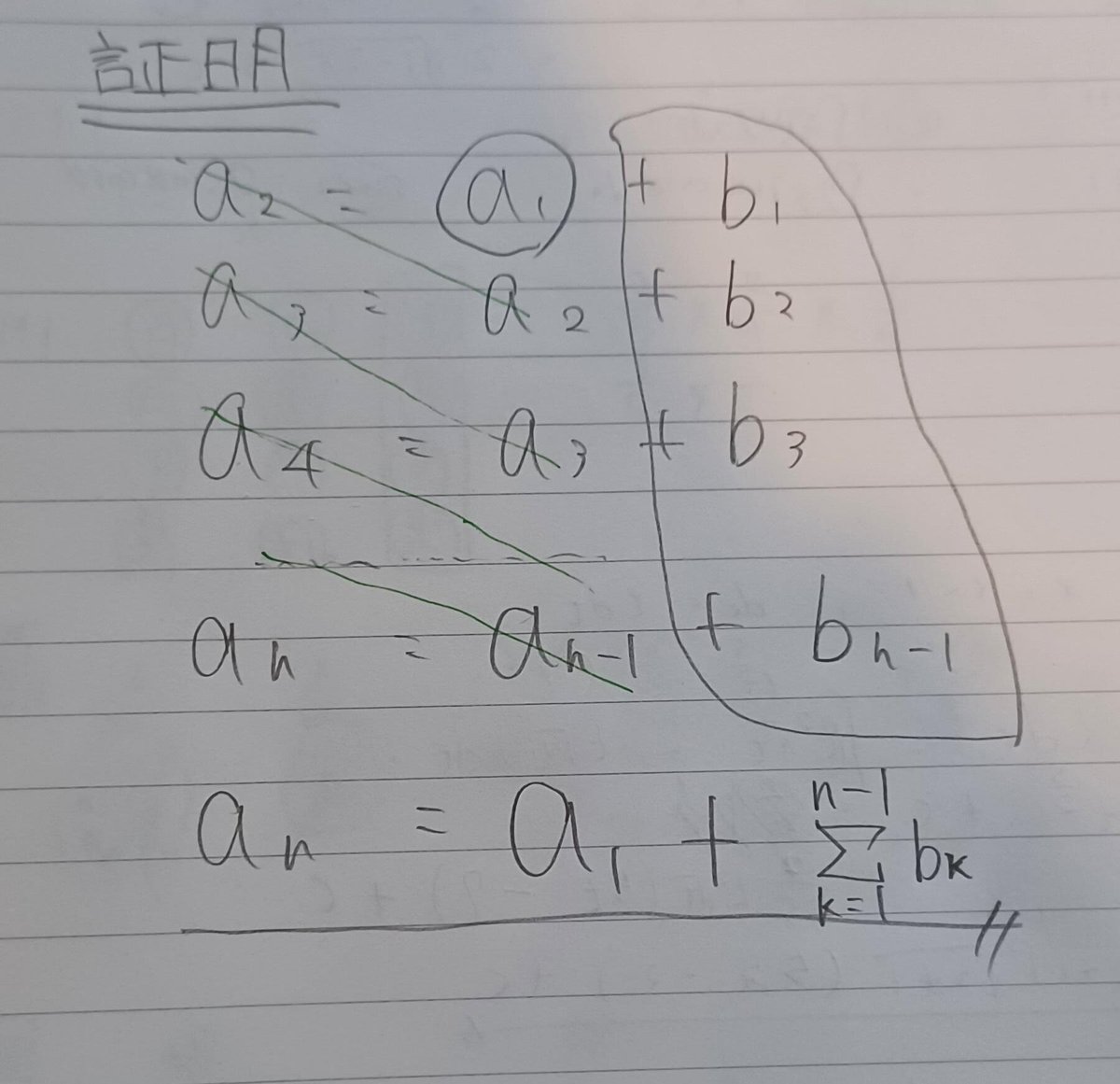
最後に

最初の基本の3パターンは何かの公式というわけではなくて、漸化式の発展を解く時に最終的にはこの基本の3パターンの形になります。自分もまだまだ勉強中なので、誤りなどありましたらコメントなどでご指摘お願いします。