
因果関係は相関関係の一部ではない
相関関係と因果関係
相関関係と因果関係は異なる。これは統計やデータ分析を学ぶと、初めのほうに出会う格言のようなものだ。この二つは異なるものなのだから、混同してはいけない、と。特に相関関係があるからと言って、因果関係があると考えてはならないと覚えておこう、と。
相関関係と因果関係は、基本的には二つの変数の間の関係について言われる。相関関係correlationとは二つの変数において、一方が変化すれば他方も変化するような関係のことを言う。因果関係causalityとは、一方が原因となって他方が結果となっている関係のことを言う。
相関関係と因果関係は異なる、ということで有名な例は、各国の年間一人当たりチョコレート消費量と、人口当たりのノーベル賞受賞者数の関係だ。

ここにはきれいな相関がみられる。相関係数も0.791と高く、統計的にも有意だ。しかし、チョコレート消費量とノーベル賞受賞者数の間に因果関係があると思う人はいないだろう。もし因果関係があるなら、チョコレート消費量を増やせば、ノーベル賞受賞者数が増えるはずだ。
(この有名な例についてのツッコミを書いておく。通常この例は、各国のGDPなりが共通原因としてあるとされる。しかし各国の科学論文発表数や、一人当たりの研究開発費、一人当たりのGDPなどに回帰して統制しても、チョコレート消費量からノーベル賞受賞者数への正の因果効果は残るという研究結果(Prinz 2020)がある。この例は意外に謎が深いようだ。)
というわけで、二つの変数の間に相関関係があるからと言って、因果関係があるわけではない。では、相関関係と因果関係はどういう関係にあるのだろう。
これについて、ネット上を調べる限り、相関関係は因果関係を包含する、因果関係は相関関係の一部であるとする記述がいくつも見られる。「相関関係と因果関係」で検索して上位に挙がるものをざっと見るだけでも、NTTコム オンライン、GMO Ask、ferret、Growth Marketing Mediaの記事にはそうした記述がみられる。

しかし私にはこれは誤った記述であるように思われる。すなわち、因果関係は相関関係の一部ではないと思われる。ということで以下、因果関係があるが相関関係がないとみなせる例を二つ取り上げて、因果関係は相関関係の一部であるとする主張への反例としよう。
反例1:非線形な因果効果
最初の例は、薬剤などの投与の場合だ。ある一定の閾値までは効果が出るが、それを超えると逆効果になるようなものがある。例えば窒素は植物の生長に効果があるが、与えすぎると逆効果になる。人間にとっても、食品や薬のなかにはそうした反応を示すものが多くある。これは、U字型の用量-反応曲線となる。
この場合、例えば以下のようなグラフになるだろう。そしてこの相関係数はほとんど0であり、相関関係はない。しかし因果関係は存在すると言える。

この反例はそこまでフェアではない。先に、相関関係は二つの変数において、一方が変化すれば他方も変化するような関係のことだと書いた。しかし通常は、二つの変数の間の線形な関係を相関関係と呼ぶことが多い。さらに、相関関係の程度の評価には相関係数が用いられるが、その中でも通常、ピアソン積率相関係数が使われることが多い。したがってこの反例は、あくまで相関関係をピアソン積率相関係数とみなしたときに有効なものだ。
さらに、非線形な因果効果を用いたこの反例は、単に非線形な関係をピアソン積率相関係数が捉えられないと言っているだけで、相関関係と因果関係というトピックに限った反例ではない。それでも因果関係は相関関係の一部とする議論に疑問を投げかけるものだろう。
ちなみに、この種の反例であれば、統計を学ぶ者なら誰もが持っているはずの本に書いてある。
相関関係とは二つのデータ間の直線的な関係のことであるが、因果関係には直線というような単純な関係ではなく、はるかに複雑な関係も含まれる。したがって、因果関係であっても相関関係にはなく、相関係数の値も低くなるものもある。
反例2:因果効果が打ち消される場合
こちらの例のほうが面白いだろう。こんなグラフになる例だ(実際のデータではない)。これも相関係数は0.06と弱く、ほぼ相関関係は無いと言える。そしてこれは非線形な関係でもない。
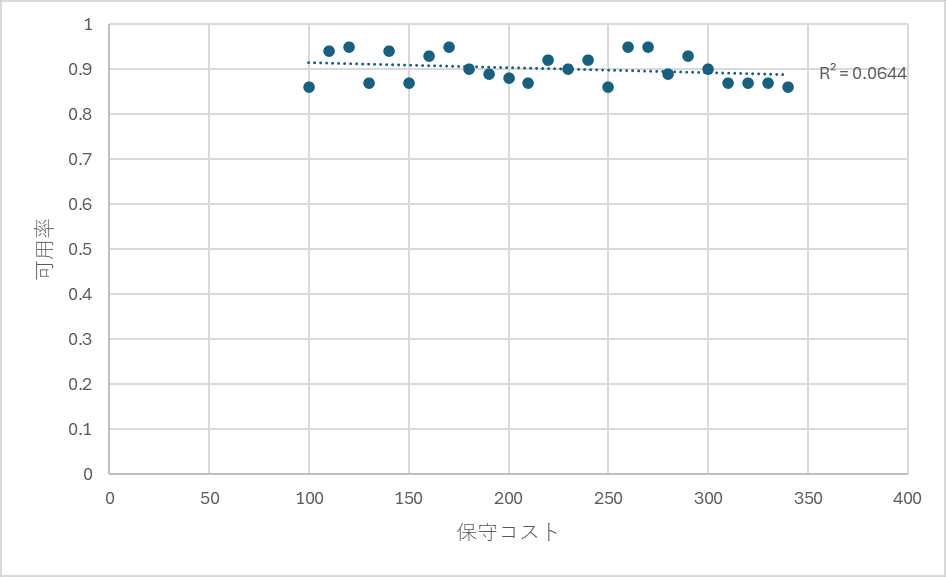
この例は、機械の保守コストとその機械の可用性を年別にプロットしたものだ。個々の点は一年間の値にあたる。この例が仮定しているのは、機械は経年劣化によって徐々に壊れていくので、同じ可用性を維持したかったら保守コストは年々増大していく、というものだ。
この例では因果関係があると言っていいだろう。まさに保守コストをかけているから、可用性が維持されているのだから。結果として、保守コストと可用性の間に相関がみられないデータが得られる。経年劣化という、保守コストによる因果効果を打ち消すような効果が存在する場合だ。
終わりに
因果関係は相関関係の一部であるとする説への、二つの反例を書いてきた。どれだけ説得的な反例と読み手が感じるかは分からないが、私自身はだいぶ整理がついた思いがする。
結局は因果関係とは何かというのが、とても難しい。ここでは素朴な反事実条件的意味付けを与えているつもりだが、分析性や第三の因果などややこしい話が控えている。その辺は哲学という泥沼に入り込むのでここまでにしておこう。
追記。
考えられるコメントとして、相関関係は単に二つの変数の何らかの関係があることを表すだけだから、関係がない$${(R^2 \simeq 0)}$$ことも無の相関があると考えれば、相関関係は因果関係を包含する、というものがある。しかし、その場合には次の二つの疑問が生じる。
その場合、相関関係はすべてを包含してしまうことになり補集合が存在しなくなるので、ベン図で書くことは適切ではない。
そう考えるなら、因果関係もゼロの因果効果がある関係としてすべての変数の間に考えることができる。
