
「五枚目の数字づくり」で「どんな計算をしてもよい」とは・・・他
6/22出題の「五枚目の数字づくり」はこうでした。

例えば、8÷4=2、5-5=0、2+0=2
つまり、「8÷4+5-5」と言う計算をすれば、五枚目の数字である「2」を作る事ができます。
他のやり方もあります。
まず、8÷5で、1あまり3と計算します。
あまりの「3」を5から引くと、2
そこで4÷2を計算すると、2。
やはり、五枚目の数字の「2」ができます。
え?、「あまり」なんか使っていいの?
それ、割り算の「答え」じゃないじゃん?
問題文には、「どんな計算をしてもよい」と書いてありますが、
足す、引く、掛ける、割るの、いわゆる「四則計算」だけを使いなさいとは書いていません。
プログラミング言語のPythonでは、あまりを求める演算子は、「%」です。
Pythonでは、8÷5は、8/5と書き、答えは1.6です。
あまりを求める演算子「%」を使うと、
8%5=3
になります。
つまり、Pythonでは、割り算をする「/」も、あまりを求める「%」も一種の演算子で、「割り算をする」事と「あまりを求める」事の間に、優劣はありません。
ポーカーチップを並べてみると、
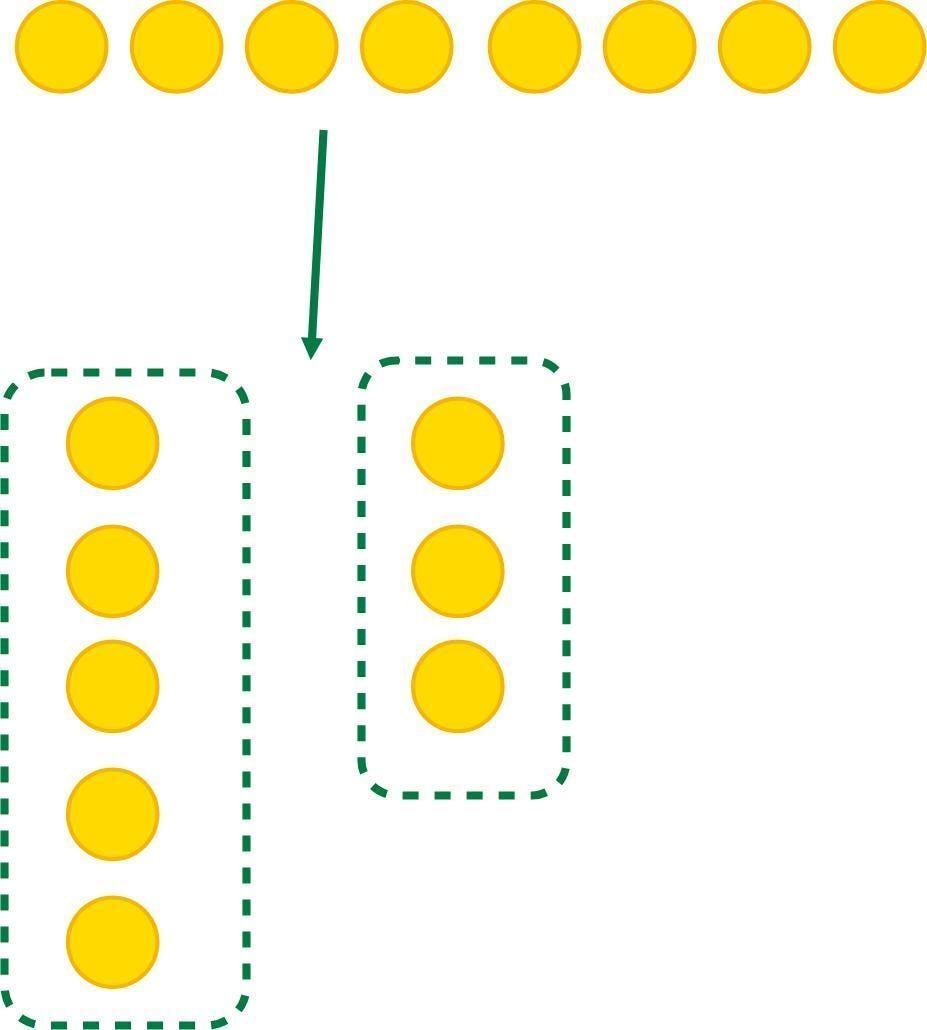
8個のチップを「5列」に並べると、1個づつ並び、3個が残ります。
この状態が8÷5=1あまり3の状態です。
あまりの3個を更に割ろうとすると、

あまりの3枚の黄色のチップをそれぞれ赤のチップ10枚と交換し、

30枚の赤のチップを5列に並べ替えると、各列とも黄色のチップ1枚と赤のチップ6枚が並ぶ、
つまり、「1.6」の状態が出現します。
割り切れる割り算 8/5=1.6 と
あまりを求める8%5=3 は、
どちらもチップ(数)を並べ替え(操作)しているだけです。
チップ(数)を並べ替え(操作)した結果、「ある状態」
例えば、8÷5の計算で黄色のチップと赤のチップの総枚数ではなく、
5列に並べた時の1列毎のチップの状態(黄色のチップ1枚と赤のチップ6枚=1.6)を「答え」だとしているわけです。
そんな事をしたら、どんな事をしたって答えが求められちゃうじゃないか?
インチキだ!?・・・
違います。
どんな計算をしたっていいって言うルールだから、割り算じゃなくて、あまり算でもいいんです。
じゃあ、聞くけど、8÷5を少数以下まで計算して、答え1.6になった
その1.6ともう1枚の「5」のカードの数字を使って、1.6×5=8、
8÷4=2
これでも5枚目の数字「2」が作れるけど、これでもいいのか?
ハイ、いいです。少数や分数を使うなとはどこにも書いていません。
今の計算は、
8÷5×5÷4=2
と言う計算をしただけです。
大事な事は、「四則計算」や整数にこだわることではなく、
こうやって、いろいろな計算方法を示して、
子どもたち(大人たちもかもしれませんが・・・)の世界を無限に広げてあげることです。
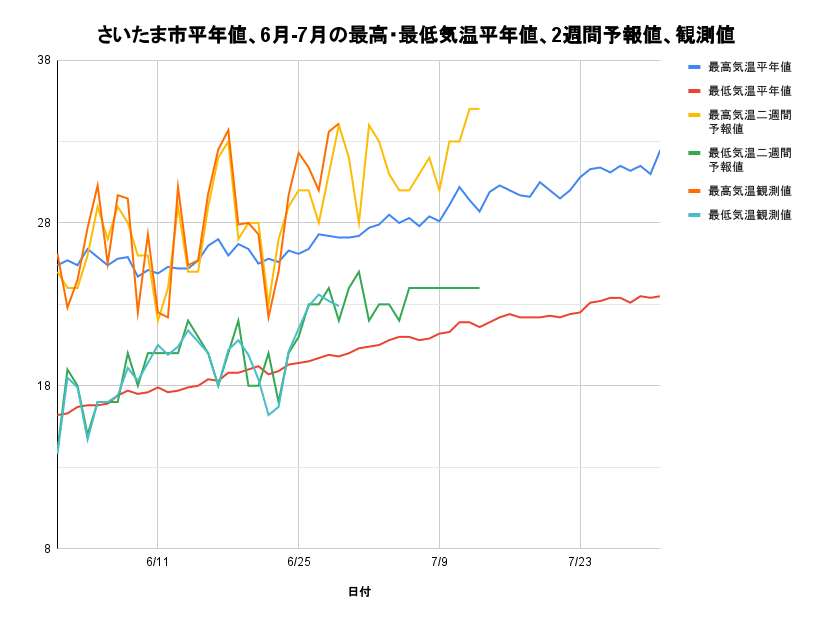
昨日は、最高気温34.1℃と猛暑日一歩手前まで気温が上がりました。
この先も連日、最高気温30℃以上の真夏日がほぼ連日続き、猛暑日に近い状態の時もある、そして、7月中旬に入ると、35℃以上の「猛暑日」となる・・・
今年の「梅雨明け」は、猛暑日が続く状態が生まれる事と同じ意味かもしれません。
とにかく、「梅雨明け」前に有色米の「田植え」と言うか、畑植え、水路植えですが、をしたいと思います。

さて、今日の5枚目の数字づくりのお題は、3,6,11,2を使って10を作るです。
どんな計算をしても構いません。頭の中で計算していないで、ポーカーチップを並べたり、積んだりしてやってみましょう。
プログラミングや表計算で使われている「関数」は、ポーカーチップをどういう風に並べ替える動きなのか?、考えてみましょう。
この記事が気に入ったらサポートをしてみませんか?
