ポーカーチップ算数と数遊び、プログラミング他

２X＋３Y＝１５になるようなXとYの組み合わせを考えなさい。

（ただし、X、Yは自然数とします。）

と言う問題について、

X＝１だと、Y＝13/3 、Yが自然数でないので駄目

X＝２だと、Y=11/3 、Yが自然数でないので駄目

X＝３だと、Y=9/3＝3 、Yが自然数になるからよい

X＝４だと、Y＝7/3 、Yが自然数でないので駄目

X＝５だと、Y＝5/3 、Yが自然数でないので駄目

X＝６だと、Y＝3/3＝１ 、Yが自然数になるからよい

X＝７だと、Y＝1/3 、Yが自然数でないので駄目

X＝８だと、Y＝-1/3 、Yが自然数でないので駄目

X＝９だと、Y＝-3/3 =-1、Yが自然数でないので駄目

ってやって、

答え：X=3とY=3の組み合わせ、X=6とY＝1の組み合わせ

と回答するのをどう思いますか？

僕は「アリ」だと思います。

たぶん、普通の数学の授業では、

３Y ＝ 15-２X

X＞15/2だと、

15-2X＜0になるので、

Yは自然数でなくなる

だからXは7より小さい

Y＝15/3-2/3X

＝5-2X/3

とすると、Xは3の倍数でないとYは自然数にならない。

ゆえに、X＝3、または6

X＝３の時、Y＝3、X＝6の時、Y＝1

答え （X、Y）＝（３,３）、（３,６）

みたいに答えないと「マル」をもらえないかもしれません。

最初にやったような方法・・・

とにかく、X＝１から順に書いていくようなやり方だと、「まぐれ当たり」だとか、「ちゃんと考えていない」とかと言われて、「バツ」になってしまうかもしれませんね。

でも、僕は、X＝１から順に書いていってもよいと思うのです。

なぜかと言うと、この問題をコンピュータに解かせる場合、

２X＋３Y＝１５になるようならマル

ならなければバツみたいな

条件を与えて、計算させると思います。

コンピュータはX＝１、X＝２・・・って順に計算していって、

X＝３とX＝６の時にマルになるって言うようにお返事すると思います。

たぶん、プログラミングを覚えると、

多少、式を変形して、

Xが8より小さい間は、計算しなさい（while X<8とか）

みたいな文を書いて、Yが自然数なら(if文)True、

そうでない時(else文とか）はFalseってお返事しなさい

ってやると思います。

つまり、プログラミングって、片っ端から順に計算するのを高速でやらせているだけだと思います。

コンピュータはすごーく計算速度が早いので「片っ端」法でもアッという間に答えを出してしまうのです。

そして、そう言う風に計算させればよいって理解していれば、後は、RubyでもPythonでもいいですが、その手の「言語」を覚えれば大丈夫です。

と言うか、「言語」を覚えなくても、表計算ソフトに、「式」を入れてあげても出来ると思います。

とにかく、「片っ端」法はコンピュータがやっている事と大差ないのです。

ですから、プログラミングの授業で「片っ端」法のプログラミングをしたら、よく出来ましたってマルをもらえると思います。

しかし、算数や数学の授業では「バツ」になってしまう、これはなぜなのでしょうか？

それは、たぶん、算数や数学の先生は、「片っ端」からやってたまたま合ったと言うだけでは、理解していることにならない、分かっていないと考えるからだと思います。

では、「理解している」、「分かっている」ってどういう事でしょうか？それは、数と数の関係を理解していると言うことだと思います。

つまり、2X+3Y=15と言う式でXが8以上になったらYはマイナスの数になってしまいます。だから、Yが自然数（プラスの整数）であるためには、Xは7以下でなければならない

みたいな事が「数と数の関係」だとして、そこが「分かっています」って言う回答でないと「数学の問題の答え」として認めないと言う発想があると思うわけです。

ところで、僕はこの文章の中で、答えの事を「回答」と書いています。普通、数学の問題集には「解答」と書かれている事が多いのではないでしょうか？

「解答」は「解いて答える」で、「回答」は単なる答えです。

数と数の関係を理「解」して答えるから「解答」と言う漢字を当てはめているのだと思います。

しかし、コンピュータは「片っ端」法で答えを求めていて、プログラミングでは「片っ端」法がアリなんだとすると、

算数や数学の答えで、「片っ端」法はダメで、「ちゃんと計算した」っぽく書くとマルになると言うのは、

先生の方が、「『この子は数と数の関係を理解している』とみなせる」と判定できるかどうか？

「片っ端」法だとまぐれ当たりなのか、数と数の関係を理解しているか、先生の方で見分けがつかないのでバツ・・・

要するに先生の都合で正解が決まっているんじゃないかとも思うわけです。

そうなると、「解答」じゃなくて、「回答」と言う漢字の方がよいかもしれない、先生が理解出来る答えと言う意味で「回答」と言う漢字を使ってみることにしたわけです。

さて、ポーカーチップ算数で、この問題を取り上げるとしたら、

こんな風にやると思います。

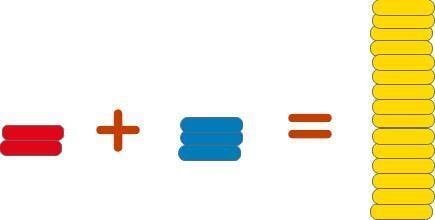
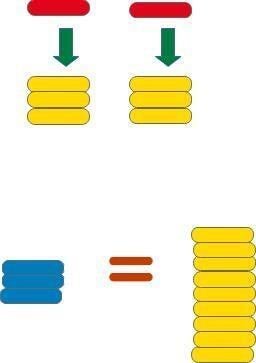
赤のチップ2枚と青のチップ3枚で黄色のチップ15枚になるとすると、赤のチップ1枚、青のチップ1枚はそれぞれ黄色のチップ何枚と交換できるでしょうか？

例えば、赤のチップ1枚を黄色のチップ1枚を交換すると、

上の図のように青のチップ3枚に黄色のチップ13枚を割り当てることになります。

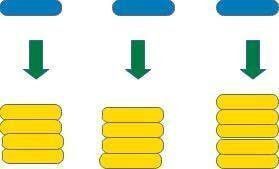
すると、青のチップ1枚づつに黄色のチップを同じ枚数づつ割り当てることができません。

では、赤のチップ1枚に黄色のチップ2枚を割り当てるとどうなるでしょうか？

今度は青のチップ3枚に黄色のチップ11枚が割り当てられることになります。

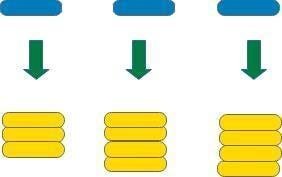
やはり、青のチップ1枚づつに同じ枚数づつ黄色のチップを割り当てることができません。

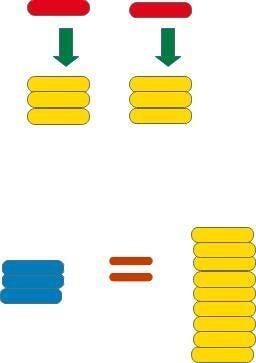
では、赤のチップ1枚に黄色のチップ3枚を割り当てるとどうなるでしょうか？

青のチップ3枚に対して、黄色のチップは9枚残っています。

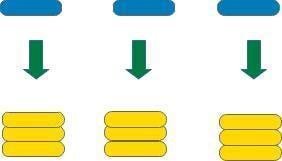
すると、青のチップそれぞれ1枚づつに黄色のチップ3枚づつを割り当てることが出来ます。

だから赤のチップ1枚と黄色のチップ3枚、青のチップ1枚と黄色のチップ3枚と言う交換が成り立つことが分かります。

こうやってチップを動かしているうちに、赤のチップ1枚に割り当てる黄色のチップの枚数が1枚増えるごとに、青のチップ3枚に割り当てられる黄色のチップの枚数は2枚づつ減っていくとか、

青のチップは3枚あるんだから、黄色のチップが3で割れる数だけ残らないと同じ枚数づつ割り当てることができないとか、

「数と数の関係」に子どもたち自身が気づいていくのではないでしょうか？

こうして数と数の関係に気づいた子どもは、今度は、プログラミングや表計算ソフトの使い方を学べば、コンピュータに対する「指示の出し方」も上手になるかもしれません。

2週間予報は、6/13は最高気温29℃と真夏日一歩手前、6/17は28℃とやはり真夏日に近く、6/18-19は31℃と真夏日、その後も27℃-28℃の日が続くとしています。

やはり、高温化して「6月中に真夏状態」は現実のものになりそうです。

夏野菜はかなり早く育つかもしれません。