「『１１と２』が二組ある」も「答え」だと言うこと

7/27の「５枚目の数字づくり」のお題はこれでした。

パッと見て、「１１と２」が２枚づつあると気づいた人も多いと思います。それで、子どもたちが「１１と２」が２つづつあるね、って言ってきたら、そう、それも答えだよと言ってあげる・・・

そういうのも「アリ」だと思うわけです。

どうして、「１１と２」が２つづつあるが「答え」になるかと言うと、

（１１、２）、（１１、２）と言うように、４枚のカードの数字を全部使って、１１と２の組を２つ作れるからです。そして、最後に「２」組作れたの「２」が答え＝（五枚目の数字である「２」を作った）といえるからです。

え？、足し算も引き算も掛け算も割り算もしてないじゃん？、そんなのおかしい？

ですって・・・。

問題文に書いてあるルールは、「４つの数字を１回づつ全部使う」、「どんな計算をしてもかまいません」です。

そして、１１と２の組を２つ造るは、4つの数字を1回づつ全部使っていますし、ある種の「計算」をしているから、「正解」になりうるのです。

実際にポーカーチップを並べて「計算」をやってみると分かります。

例えば、２＋１１は、

２枚のチップと１１枚のチップを別々に積んだ後、両方を一緒にして１３枚のチップが積まれた状態にしています。

また、２×１１を計算する場合は、

２枚づつ積んだチップの「山」を１１個並べる事で出来ます。

つまり、「計算」とはあるルールに従って、チップを並べている事に相当しています。「計算」の中で出てくる「２」とか「１１」とかと言う数字は、２個づつチップを「積む」とか、１１列「並べる」とかと言う「操作」の時に使われているわけです。

ある数についての計算は、その数についての何らかの「操作」をしている事であって、「＋（足す）」とか「×（かける）」とかと言う「記号（計算の種類）」は、その操作がどういうものかを示していると考える事が出来ます。

では、２と１１の組を造るのはどうでしょうか？

チップを２枚積んだ山と１１枚積んだ山で「組」を作っていますね。

これで、（２、１１）と言う「結果」を造った事になります。

「『２』と『１１』から（２、１１）を造る」と言うのは、「２＋１１」や「２×１１」と同じ立派な「計算」なのです。

え？、でも、２＋１１＝１３、２×１１＝２２とある「数」が出来るけれども、（２、１１）は、ただ２つの数が並んでいるだけで「数」になっていないじゃないか？

ですって？

（２、１１）は、「ベクトル」と言う立派な「存在」です。

［ベクトルに対して、２、１１、１３、２２などの「単独」の数はスカラーと言います。］

問題文にはどこにも「ベクトル」を使ってはいけないとは書いていません。スカラー（数）を組み合わせてベクトルを造る「操作」をするのも立派な「計算」です。

では、以上のような説明をして、子どもがこう聞いてきたらどうすべきでしょうか？

じゃあ、足し算とか引き算とか掛け算とか割り算じゃなくても、どんな「計算」でもいいの？

いいよ。でも、その計算がどういうものか、ちゃんとチップを積んだり、並べたりして、見せてね。

チップを積んだり、並べたりすることは、その操作方法を「明示」することです。

自分の空想の世界で勝手に思ったと言うのではなく、他人にそのルールが伝わるように示す事です。

スポーツでもゲームでも、参加する人には「ルール」が分かるように示されています。あるルールに従って「操作」することを「関数」として定義して、「関数」によって、「オブジェクト（対象）」を動かしていくのが「プログラミング」です。

「ここにトランプが1組じゃなくて、1000組あるとする。（２、１１）の組は全部で何組できる？」って聞いてみたら、子どもたちはどう答えるでしょうか？

ポーカーチップとトランプを使った「算数」は、とても広い世界に子どもたちを導いていくことができるのです。

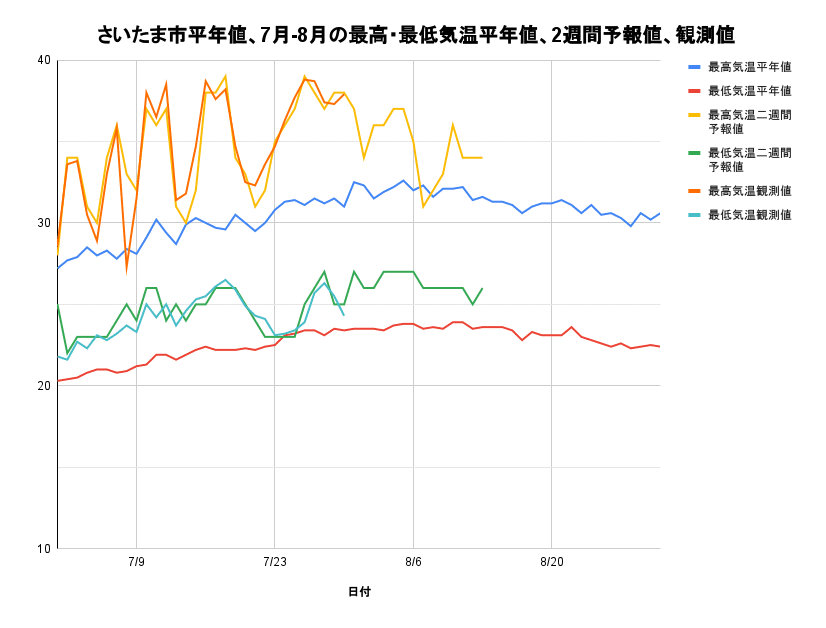
2週間予報は、立秋（8/7頃）から百日目（立夏から100日後＝8/12頃）まで連日、雨が降るとしています。

どうやら、「雨の音にぞ驚かれぬる」立秋になりそうです。夏ニンジンの種まきチャンスかもしれません。

五枚目の数字づくり、本日のお題は、「１」、「１１」、「１２」、「４」を使って、「７」を造るです。

頭の中で考えていないで、実際にポーカーチップを積んだり、並べたりしてやってみましょう。