重力質量エネルギーの導出
(E = m₉ c²)を使うと、よくアインシュタインの相対論を真似たと言われることもあるので、ちゃんと導出過程で以下の世界一有名な式(E = m c²)との違いを見せておこうと思う。
物体は、どんな形ででも、エネルギーを吸収したり放出したりすると、E=MC²の式に基づいて、その質量も増加したり減少したりする。1905年アインシュタインは特殊相対性理論を発表し、このことが基本原理から導出されることを示した。
まずは電磁気学から.
屈折率(くっせつりつ、英: refractive index[1])とは、真空中の光速を物質中の光速(より正確には位相速度)で割った値であり、物質中での光の進みかたを記述する上での指標である。真空を1とした物質固有の値を絶対屈折率、2つの物質の絶対屈折率の比を相対屈折率と呼んで区別する場合もある。
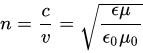
ここでμ、εは材質の透磁率、誘電率
μ0、ε0は真空の透磁率、誘電率
ここで記号と意味を、絶対静止基準系+電磁気学 → 光速度基準系+電磁気学へ、以下の考えかたにより、
屈折率(n)は、観測者と異なる系の真空中の光速はスケールにより変化するので相対速度因子(γ)に、
物質中の光速(v)は、運動ではなく波動なので波動速度(w = f λ)に変える。
次にカウフマンの実験から.
次に1901年、アインシュタインの相対論より前の「運動エネルギーによる質量増加の検証となったカウフマンのベータ線屈曲の実験」から、

m₁ = m₀ c / √( c² - v² ) = m₀ c / w = γ m₀. (1)
運動(v)により波動速度(w)が低下し、静止質量(m₀)が相対速度因子(γ)の変化により慣性質量(m₁)が増加したとする。
※この時点では、相対論的質量と同じようにエネルギーの増減とスケールの変化の区別がついてない。
またニュートン力学から.
次にニュートン力学の第二宇宙速度(脱出速度:v² = 2GM / r)は、
この物体に、負の位置エネルギーを打ち消す速さ v₂ の運動エネルギー(1/2)mv² を与えれば無限遠に達する、即ち地球の重力圏から脱出することができるとして求める。
式(1)へ、観測基準系に重力ポテンシャルを考慮すると、
w² = c² ± 2GM / ( r + h ) ± v². (2)
波動速度(w)は、重力ポテンシャルの地表面からの高度(h)で運動エネルギーを得る、もしくは摩擦によって運動エネルギーを失うことも考慮した形となる。
式(2)を宇宙論的に、何処にでも何時にでも光速度基準系の観測者を置けるよう(v² = 2GM / r )に置き換えると、
w² = c² ± v². (3)
また式(1)の静止質量(m₀)は重力質量(m₉)に置き換えられ、カウフマンの実験では電子のため曖昧だった、重力質量はエネルギーの増減、慣性質量は相対速度因子(γ)の変化、が区別できるようになる。
※相対性理論は、式(1)の時点で光速度(c)と波動速度(w)の違いを光速度不変の原理で縛るので、その区別ができない。
γ = m₁ / m₉ = c / w = c / √( c² ± v² ). (4)
これを光の(運動量の)等価原理とする。
最後に量子論から.
そこで運動量密度とかエネルギー密度とか言っていた概念は光の粒が持つ運動量とエネルギーという概念で置き換えられることになる。すなわち、光子はエネルギーEと運動量pを持つ粒子であり、その間には、
E = c |p| = h f. (5)
※ここで振動数(ν)は、運動速度(v)と間違いやすいので周波数(f)にする。
式(4)、(5)から重力質量とエネルギーの等価式は、

E = c |p| = h f = m₉ c² = γ m₁ w². (6)
これからエネルギーや光の運動量をどれで表現しても、表現の自由が成り立つのは言うまでも無い。
※ミクロの世界でも、重力質量(m₉)と慣性質量(m₁)の違いを光速度不変から抜け切れてない一般相対論は、以下のような問題から抜けきれない。
実はうまくいかない理由はある程度わかっています。これは質量を持つ物体の「大きさ」が一般相対論と量子力学で反対の振舞いをすることに関係しています。一般相対論によるとブラックホールの大きさは質量に比例します。一方,量子力学によると物体は波のように振舞い,その波長はその物体の質量に反比例します。つまり,物体の大きさの目安となる長さは,重力では質量に比例し,量子論では質量に反比例する,という具合に完全に反対になっていて,これが重力と量子論を一緒に考えることが難しい原因なのです。
