数値群論テーブルでコラッツ予想の証明

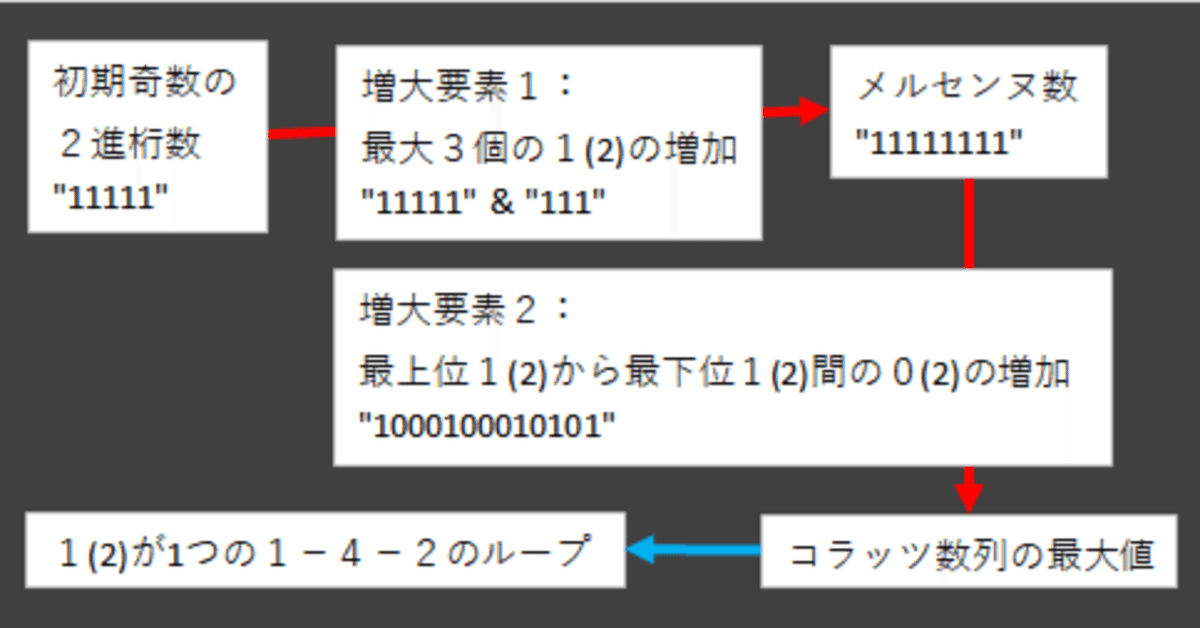
コラッツの予想は、初期奇数の２進数の１の個数が増減しながら、最終的に１個（１－４－２のループ）になるゲームである。

初期奇数の２進桁＋最大３個の１の増加幅

以下は、コラッツ数列のショートカット（［３ｘ＋１］／２）が奇数ならそれを続け、偶数なら奇数になるまで一回、もしくは複数回１／２したコラッツ数列の例である。

初期値２７のコラッツ数列の８進数（太字は奇数）

33 51 76 37 57 107 153 241 362 171 266 133 211 316 147 233 351 536 257 407 613 1121 1572 675 1234 516 247 373 571 1066 433 651 1176 477 737 1317 2067 3123 4575 7074 3436 1617 2527 4003 6005 11010 4404 2202 1101 1542 661 1212 505 750 364 172 75 134 56 27 43 65 120 50 24 12 5 10 4 2 1

初期値９６６３のコラッツ数列の８進数（太字は奇数）

22677 34237 52357 77547 137433 217251 326776 153377 241177 361677 552637 1040157 1460247 2310373 3454571 5303066 2541433 4022251 6033376 3015577 4424477 6636737 12156317 17245467 26770323 42364475 63556734 31667356 14733567 23311463 35056315 53505464 25642632 12721315 20272064 10135032 4056415 6105624 3042712 1421345 2232130 1115054 446426 223213 334721 513272 245535 370414 174206 76103 135145 213630 105714 42746 21363 32155 47244 23522 11651 16576 7277 13037 20457 30707 45253 70001 124002 52001 77002 37401 57202 27501 43342 21561 32452 15225 23740 11760 4770 2374 1176 477 737 1317 2067 3123 4575 7074 3436 1617 2527 4003 6005 11010 4404 2202 1101 1542 661 1212 505 750 364 172 75 134 56 27 43 65 120 50 24 12 5 10 4 2 1

まとめると、コラッツ数列の奇数の８進数の下一桁の遷移は以下のようになる。

図１．２つ以上の１から最終的に１つだけの１のループへ

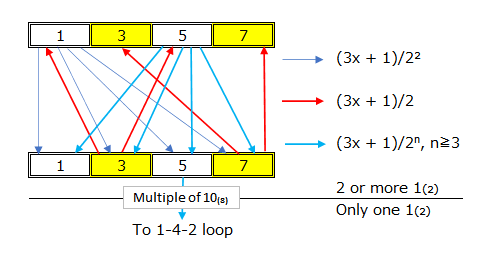
これは初期奇数の２進桁（最上位１から始まって最下位が１）に対して１～７₍₈₎の３つの１の増加幅をもって、変異することを意味する。例えば初期値２７の２進数は５桁だが増加幅を入れると８桁、初期値９６６３の２進数は１４桁だが増加幅を入れると理論値は１７桁である。

コラッツ数値群論テーブルとメルセンス数

以下のコラッツ数値群論テーブルは、２進４桁のメルセンス数（２⁴ー１＝１５）から４ｎ＋１まで２進木（黄色背景の数値）とコラッツショートカット計算（［３ｘ＋１］／２）を並べた奇数群とRoots odd zの行を０世代から順にリンクした表である。

表１．コラッツ数値群とメルセンヌ数

これはメルセンヌ数（２ⁿ⁺³ー１）以下の奇数がテーブルに一回づつ反映され、そのメルセンヌ数の少なくとも（２ⁿー１）以下の３以外のRootsOdd zが世代ごとに一意にリンクされる。つまり１からボトムアップでメルセンヌ数（２ⁿー１）以下の奇数が世代のコラッツ数値群ごとにリンクされていることを意味する。※表１の２７の行は、メルセンヌ数（２⁴ー１＝１５）ではリンクされてない。

メルセンヌ数と初期奇数と最大値の関係

初期奇数の桁+３個の１の個数を最大として、初期奇数の桁+３bitのメルセンヌ数の行の偶数の最大値（３ｘ＋１）以内でコラッツ数列は変化する。

表２．メルセンヌ数と初期奇数と最大値の関係

図２．メルセンヌ数と初期奇数と最大値の関係

メルセンヌ数と初期奇数、それぞれの最大値に比例関係がある。

結論

コラッツ予想を逆計算で１から派生できない自然数が存在する事を仮定すると、２進数で１が１つの１－４－２の０世代からメルセンヌ数（２ⁿ⁺³－１）まで数値群展開すると、少なくともメルセンヌ数（２ⁿ－１）まで世代がリンクされる仕組みは、任意の初期数の桁ｎが大きくなっても同じだから、コラッツ予想を逆計算で１から派生できない自然数が存在することと矛盾するので、コラッツ予想の正しさを証明する。