
高校入試で積分を使った話
気づけばいつの間にか日本の入試シーズン。
個人的には、高校はともかく大学の受験では結構大変な思いをしたので、この時季になるといつもなんとも言えない緊張感を覚えてしまう。
大学受験の話は一つの記事で簡単には書ききれなさそうなので、今回はとりあえず高校入試の思い出の話。
超絶難化した数学
僕の高校入試での一番の思い出は、僕が受験した年の埼玉県立高校の数学が超難化していたことだ。
僕の周りの人たちも、入試が終わった後に
「数学がやばかった」
とか
「数学のせいで落ちそう」
とか言っていた。
正直、高校入試はだいぶ昔の話なのであまり記憶に残っていないが、数学の問題を解いた時の感触はかろうじて残っている。
僕は当時数学は結構得意だったが、それでも「この問題難しいなぁ」と思いながら解き進めていた。
「そうだ、積分を使おう」
それでも、順番に問題を解き進めて、辿り着いた最後の問題。

確かこんな感じの問題だった。結構簡略化したので、恐らく実際はもうちょっと難しかったはず。
この問題を見た時の第一印象は、
「うわぁ、面倒臭いなぁ」
である。正攻法で解くならば、2つの円錐の底面の円の半径と高さを、三平方の定理で求めて計算することになる。
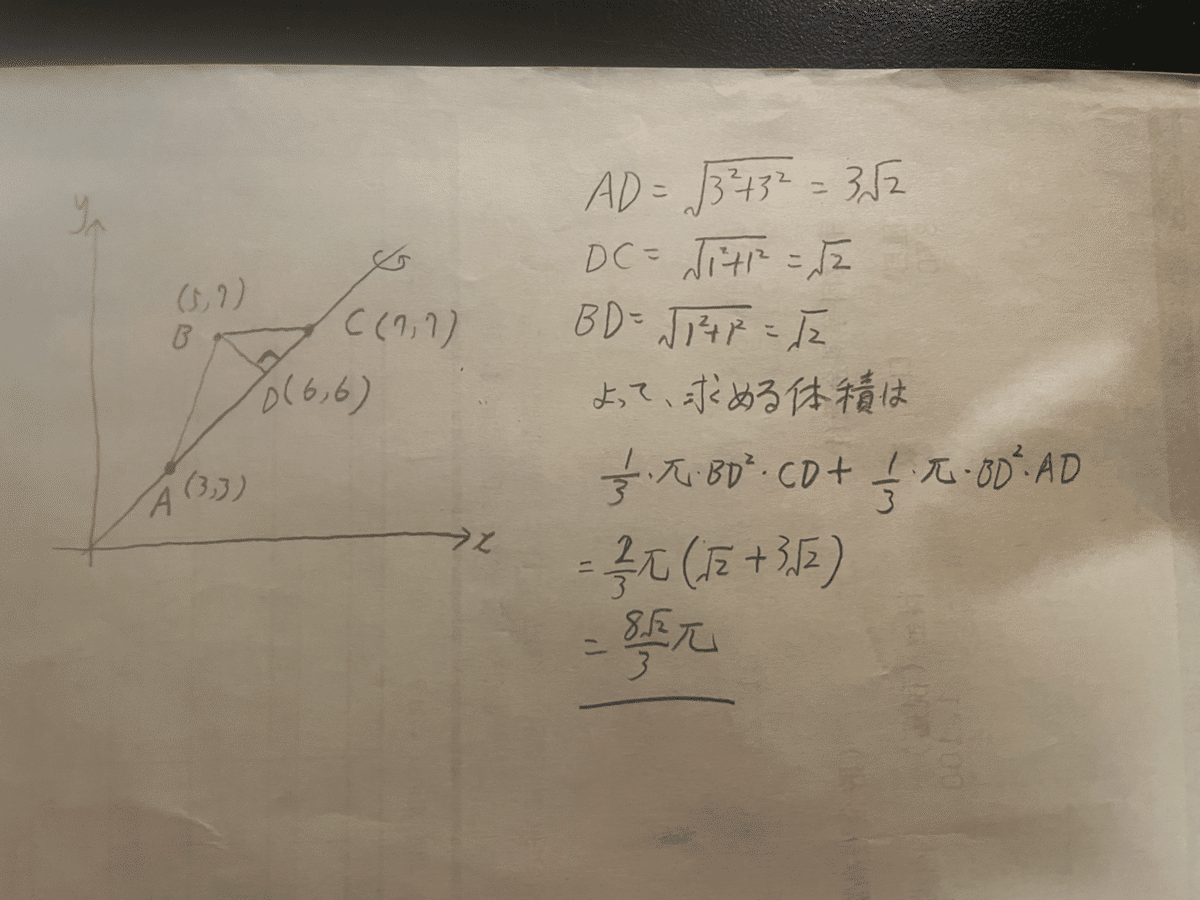
今にしてみれば、そこまで面倒ではないし、普通に解いたほうが絶対に楽である。
とはいえ、途中過程も書かなくてはならず、この考え方や式の意味などを一つ一つ説明するのが同時の僕にとっては少し面倒だった。
そこで、この面倒な作業を回避するために浮かんだアイディアが、
「積分しちゃえば良いんじゃね?」
である。

こうしちゃえば、説明を少なくして済むと当時の僕は考えていた。
しかし、見てもらえばわかるが、かえって計算が複雑になっている。説明不足な感も否めない。
とはいえ、残り時間も少なく、他のやり方を考える時間もなかったため、当時の僕は積分を採用したのだった。
結果、採点はどうだったのか
積分を使った計算結果は、果たして点をもらえるのだろうか。
入試が終わった後、結果通知という形で自分の点数を知ることができるので、確かめてみる。
結論から言えば、わからないけど恐らく部分点は貰えている、である。
埼玉の公立高校入試では点数だけは教えてくれるが、自分の答案がどうやって採点されたかまでは教えてくれない。
なので推測に過ぎないが、点数的に最後の問題で点を取れていないと計算が合わなかったので、恐らく点数は入ったんじゃないかと思う。
別に微分積分を知っている中学生自体はそこまで珍しくないだろうが、それを公立高校の入試で使用した中学生はほとんどいないのではないだろうか。
ただ、上にも書いた通り、100%普通の解き方で解いたほうが楽である。
それに、「中学で習わない方法は使ってはいけない」という方式で採点をする所もあるかもしれない。
もし微積分を高校入試で使って良いのか迷っている中学生がいるならば、
「基本的には普通に解くが、もし本当に他の解き方が何も思いつかなかったら、最悪微積分を使う」
くらいの心持ちで臨むことをお勧めする。
