【勉強法】瞬殺で答えを出す裏技公式（上級編）

二次関数の変化の割合

中学校の数学の教科書に記載されている公式は、全員が理解して覚えておく必要があるものばかりです。
今回紹介する公式は、教科書には載っていないものの、成績上位者や計算を速くしたい中学生には知っておいてほしい裏技ともいえる公式です。

基本の公式を理解できている人は是非とも覚えて使ってみて下さい。
なお、裏技公式の導出や証明は省略させてもらっています。

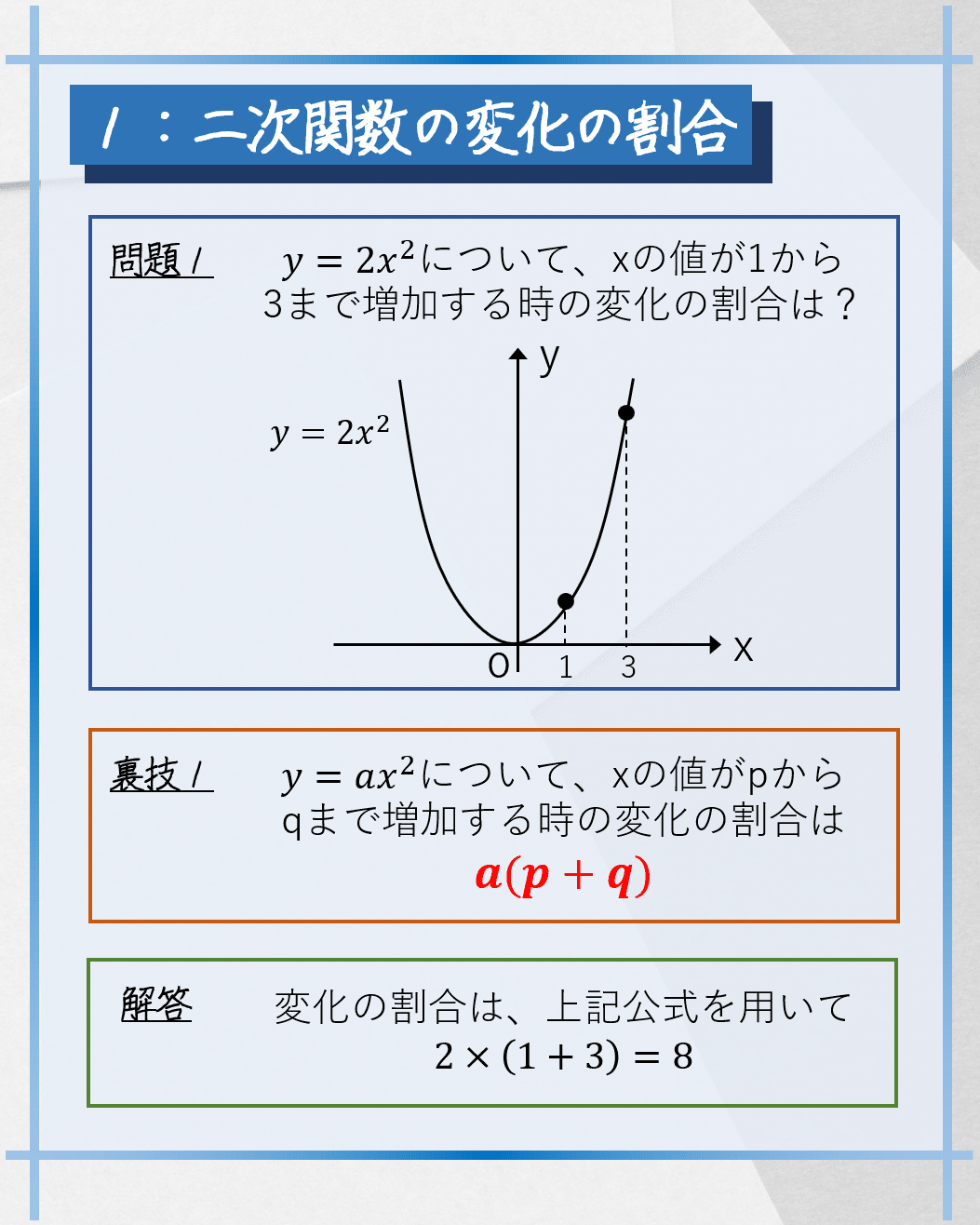
まず１つ目は「二次関数の変化の割合」です。
通常であれば、xの値に対応するyの値を求めて、xの変化量とyの変化量から変化の割合を求めますが、裏技公式ではyの値を求める必要はありません。
これだけでもかなりの時間短縮になるはずです。

---

二次関数と交わる直線の式

２つ目は「二次関数と交わる直線の式」です。
今回の問題では、点Aと点Bのy座標も記載されていますが、y座標がなくてもx座標だけで直線の式が求まるのが、この裏技公式の利点です。
通常では、x座標の値を二次関数の式に代入してy座標を求め、点Aと点Bの座標から連立方程式などを立てて直線の式を求めます。

本公式を使うとy座標を求めるまでもなく一気に直線の式が導けるので大幅に時間が節約できます。
なお、直線の式の傾きにあたるa(x1+x2)は、裏技公式１の変化の割合と同一です。

---

円錐の側面積

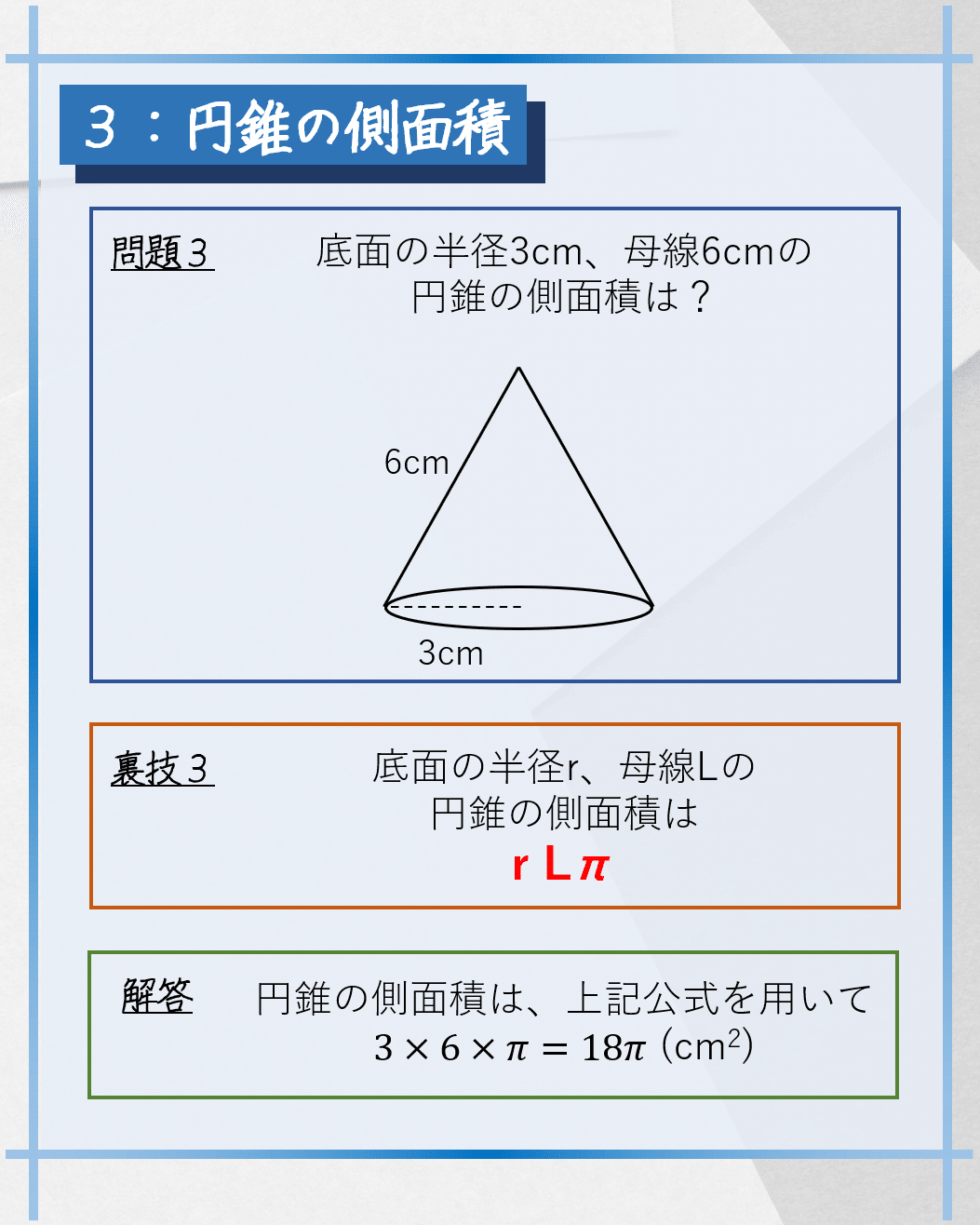
３つ目は「円錐の側面積」です。
円錐を展開すると側面は扇形で示されます。
扇形の面積を求めるには、通常は中心角の大きさを求める必要があり、手間がかかりますかります。

この裏技公式では、底面の半径と母線の長さだけで円錐の側面積を求めることができ、計算時間が短くなるだけでなく、計算ミスも圧倒的に少なくなります。
公式自体も簡単なので、是非とも覚えておいて欲しい公式です。

---

正四面体の体積

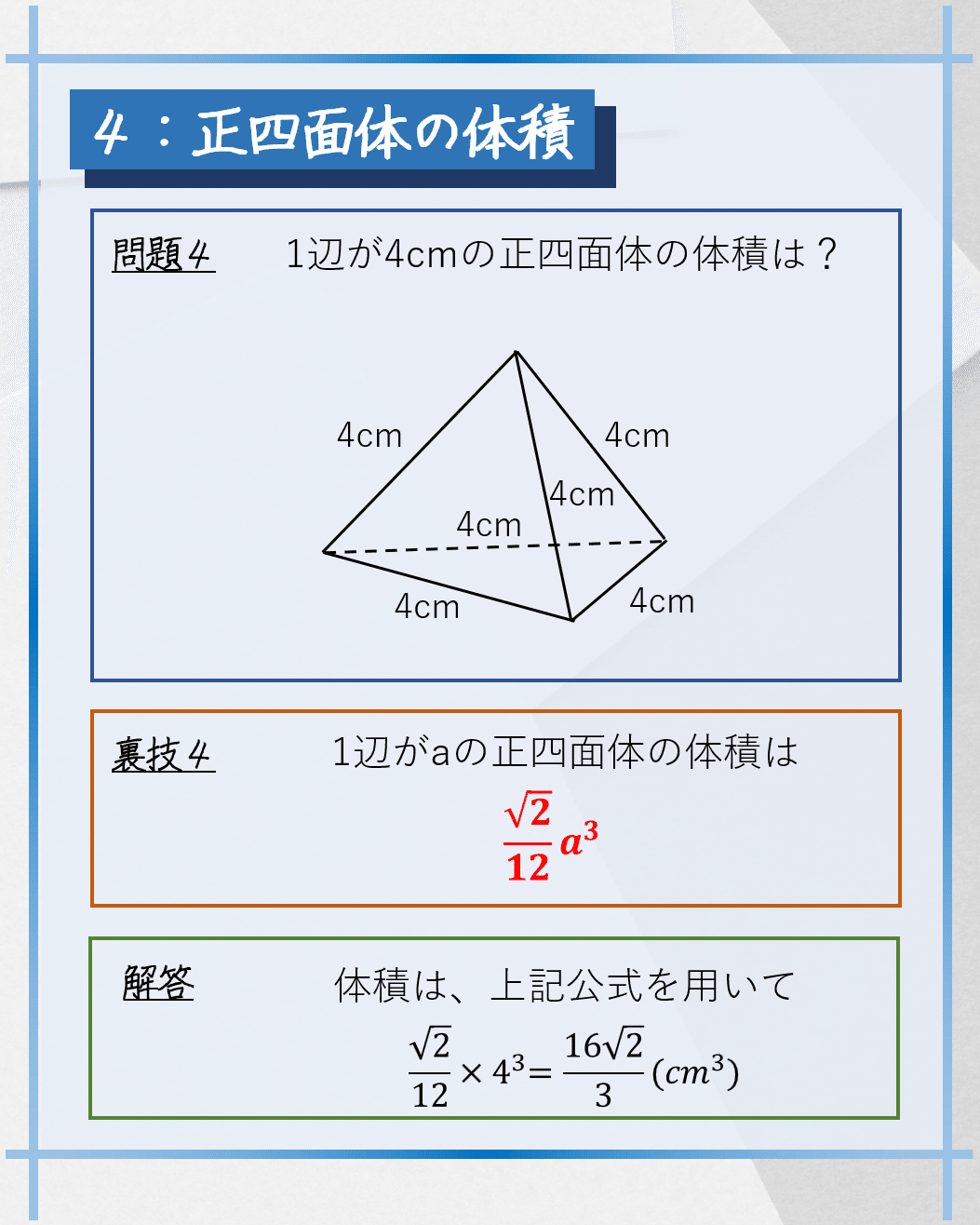
最後は「正四面体の体積」です。
正四面体の体積は、高校数学でもよく出題されます。
通常は、三平方の定理と重心の性質から正四面体の高さを求め、体積を算出するので時間がかかります。

この裏技公式では、１辺の長さのみで体積が分かるので瞬殺できます。
途中式を書かないといけない場合などは使えませんが、それでも検算に使用すると良いかと思います。

このように、裏技公式は覚えておくとミスが減り計算が速くなります。
労力がぐっと減り他の問題を解く時間が増えますので、今回紹介した裏技公式を是非覚えてみて下さい。
なお、数学の初級計算テクニックは下記コラムを参考にしていただくと、計算スピードが劇的に上がります。