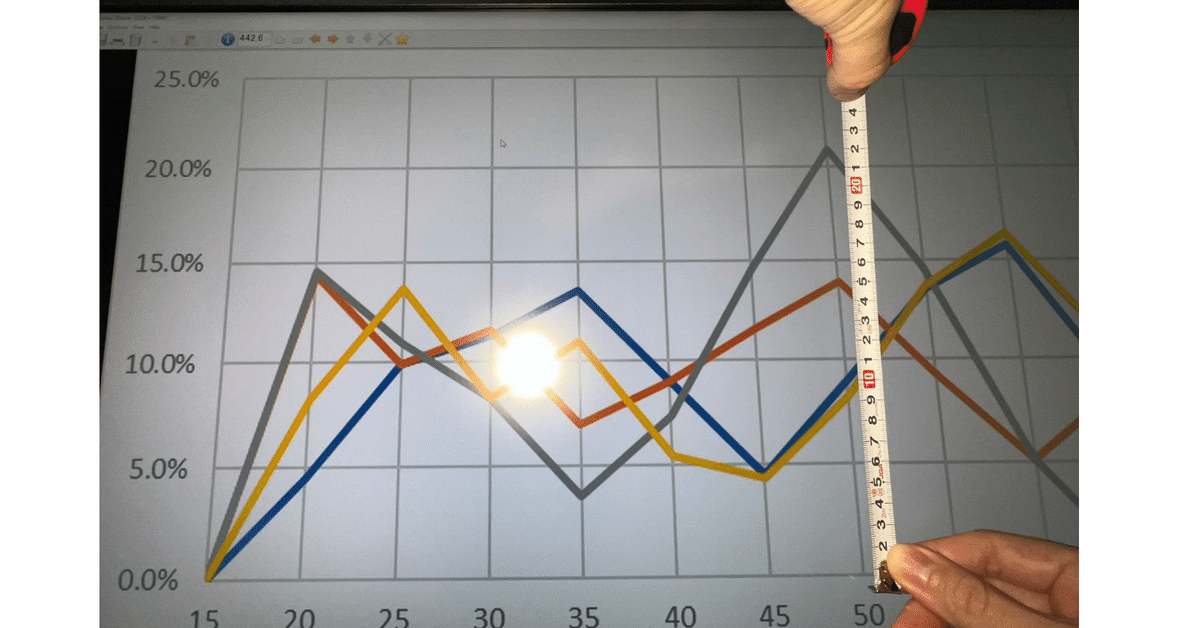
画像化された複数の折れ線グラフを無理やりデータ化
作成者:RMR(Rosso Machinelearning Reportage)
マイブーム:AtCoder(開始5ヶ月で水色コーダー到達)
特技:ルービックキューブ20秒以内
はじめに
こんにちは。株式会社Rosso、AI部です。
以前、仕事で扱ったデータの中で、画像化されたグラフを数十枚渡されたことがありました。
私の前の担当者はコレへの対処としてディスプレイに定規を当てて記録していたとのことだったが、私は嫌だったので画像からのデータ化を試みました。
その方法をチームにお話したところ大変ウケましたので、その画像化の処理についてまとめます。
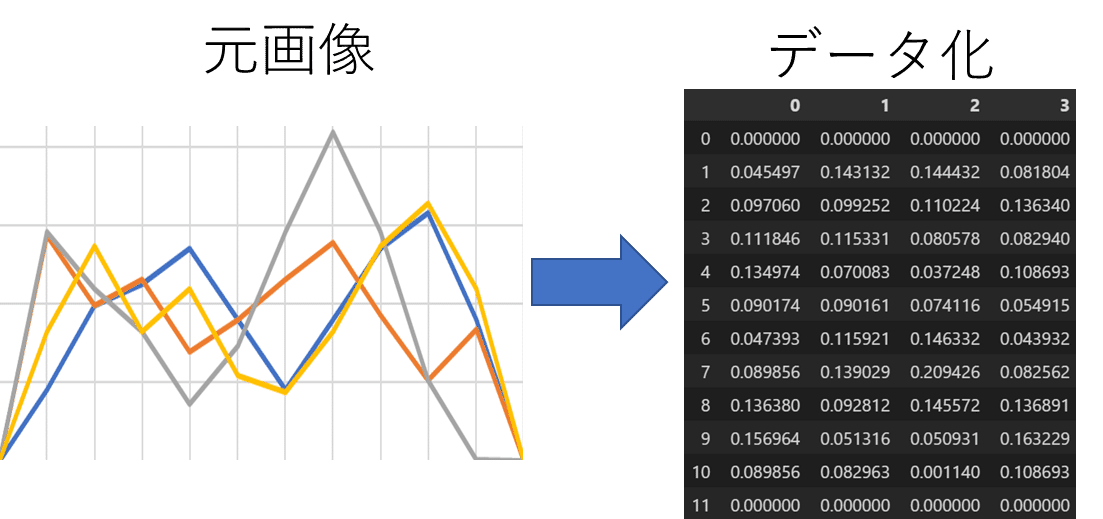
準備
準備その1_配色の取得
EXCELで作成される折れ線グラフは基本的に配色が決まっているので、色のRGB情報を取得する。
(教師なし学習で色を自動で分類できれば良かったが、配色によっては調整が必要)
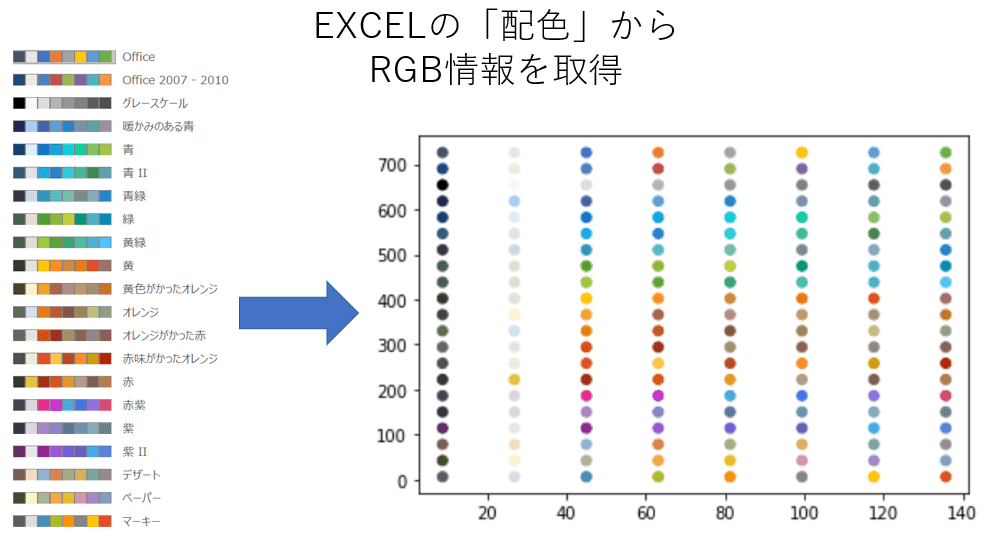
折れ線グラフの色に使われるのは左から3番目以降の色から。(左の2色は白黒相当の色)
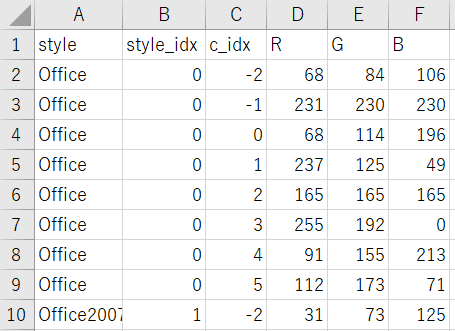
この記事内で紹介する配色の「Office」と「グレースケール」のみ値を貼り付けておきます。
import pandas as pd
df_style = pd.DataFrame([[68, 84, 106, -2, 'Office', 0],
[231, 230, 230, -1, 'Office', 0],
[68, 114, 196, 0, 'Office', 0],
[237, 125, 49, 1, 'Office', 0],
[165, 165, 165, 2, 'Office', 0],
[255, 192, 0, 3, 'Office', 0],
[91, 155, 213, 4, 'Office', 0],
[112, 173, 71, 5, 'Office', 0],
[0, 0, 0, -2, 'グレースケール', 2],
[248, 248, 248, -1, 'グレースケール', 2],
[221, 221, 221, 0, 'グレースケール', 2],
[178, 178, 178, 1, 'グレースケール', 2],
[150, 150, 150, 2, 'グレースケール', 2],
[128, 128, 128, 3, 'グレースケール', 2],
[95, 95, 95, 4, 'グレースケール', 2],
[77, 77, 77, 5, 'グレースケール', 2]],
columns = ['R', 'G', 'B', 'c_idx', 'style', 'style_idx'])準備その2_グラフ情報の手入力
データの点数、ラベル・凡例・目盛の数値などを除いたグラフの画像のピクセル範囲などを指定します。今回は手入力で済ませます。
(自動で検出したいが、今回は大変そうなので許してください)
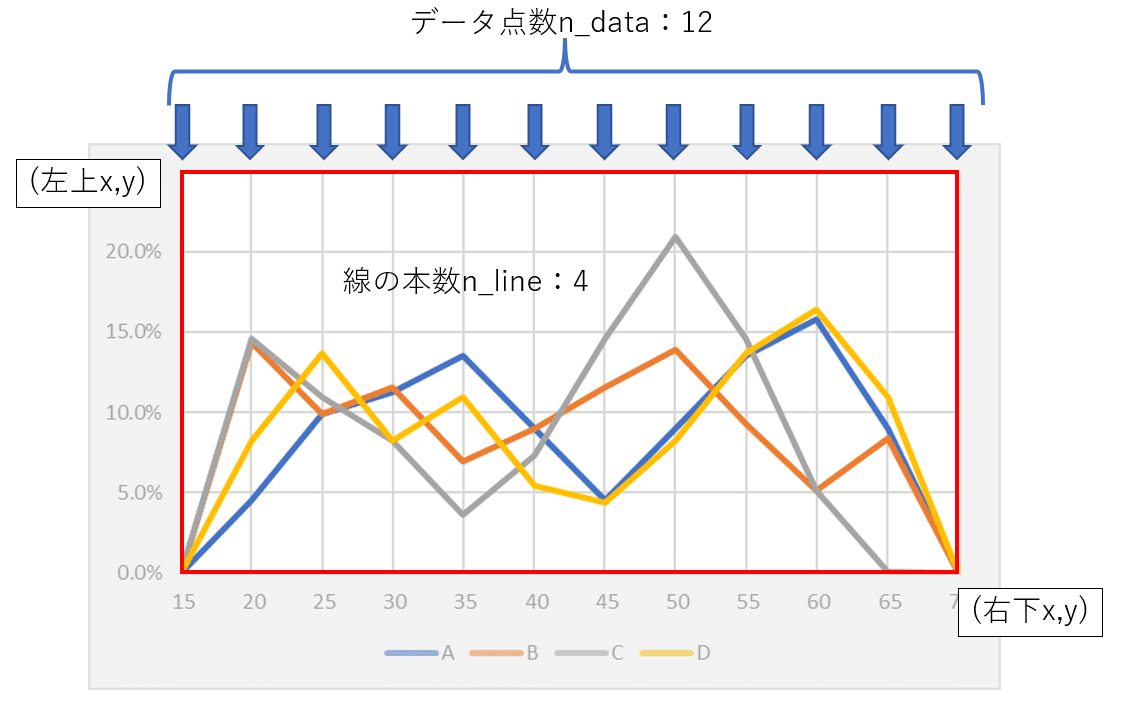
#データ数(x軸のグリッドの数)
n_data = 12
#線の数
n_line = 4
#左上x,左上y,右下x,右下y
crop = (78,24,719,355)
#EXCELのテーマ
style_name = "Office"データ化処理
画像の切り抜き
from PIL import Image
filename = "image/0.png"
img = Image.open(filename).crop(crop).convert("RGB")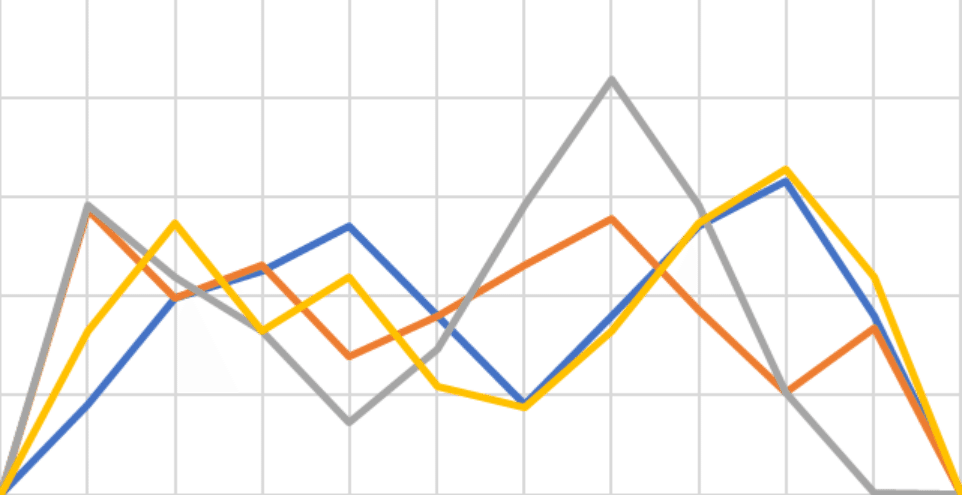
画像をnumpyに変換し、座標情報を保持
import numpy as np
img_array = np.array(img)
height,width,_ = img_array.shape #(height,width,RGB)
img_array2 = img_array.reshape(-1,3)
XX,YY = np.meshgrid(np.arange(width),np.arange(height))
XX = XX.reshape(-1,1)
YY = YY.reshape(-1,1)
img_array2 = np.concatenate([img_array2,XX,YY],1) #(R,G,B,X座標,Y座標)背景を除外(今回は白背景)
配列のほとんどは白背景のピクセル。描画が重くなるので除外。
white_th = 15 #白を除外する閾値
#背景の白を除外
white_flg = np.where((img_array2[:,0]>=255-white_th)\
&(img_array2[:,1]>=255-white_th)\
&(img_array2[:,2]>=255-white_th)\
,1,0)
#白やグリッド線除外
array = img_array2[white_flg==0]各折れ線に分割
各ピクセルがどの折れ線の色に最も近いかを計算。
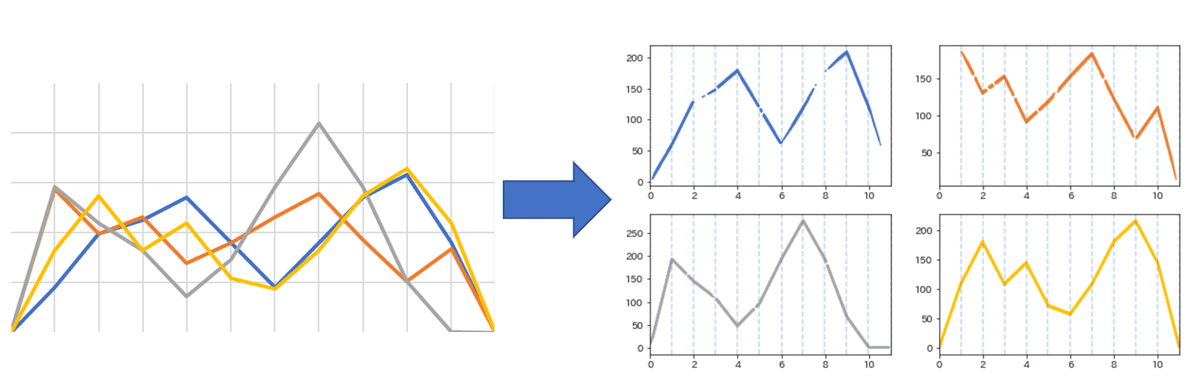
from sklearn.preprocessing import StandardScaler
from skimage.color import rgb2lab
#RGB色空間をLab色空間に変換し、各色との2乗差を取得
lab_array = rgb2lab(array[:,:3]/255)
lab_scaler = StandardScaler()
lab_scaler.fit(lab_array)
lab_array_std = lab_scaler.transform(lab_array)
diff_array_list = []
for i in range(n_line):
#先程取得しておいた配色テーマごとのRGB情報を取得
RGB = df_style.query("c_idx==@i").iloc[0][["R","G","B"]]
Lab = rgb2lab(np.int32(RGB.values.reshape(1,-1))/255)
lab_ = lab_scaler.transform(Lab)[0]
temp_diff = 0
for i in range(3):
temp_diff += (lab_array_std[:,i] - lab_[i])**2
temp_diff = temp_diff**0.5
diff_array_list.append(temp_diff)
argmin_idx = np.array(diff_array_list).argmin(0)
x_min = float("inf")
x_max = -1
line_list = []
#最も色の差が小さい折れ線に振り分け
for i in range(n_line):
temp_ = array[argmin_idx==i]
x_min = min(x_min,temp_[:,3].min())
x_max = max(x_max,temp_[:,3].max())
line_list.append(temp_)
X_list = []
Y_list = []
#各折れ線の色のどれに近いかを計算
per = 10 #テーマの配色に近い上位10%のみを採用する
for i,line in enumerate(line_list):
th = np.percentile(diff_array_list[i][argmin_idx==i],per)
temp_ = line[diff_array_list[i][argmin_idx==i]<=th]
#座標をデータ点のインデックスに変換[0,n_data-1]
X = (temp_[:,3]-x_min)*(n_data-1)/(x_max-x_min)
Y = max(array[:,4])-temp_[:,4]
X_list.append(X)
Y_list.append(Y)ノイズピクセルの除去
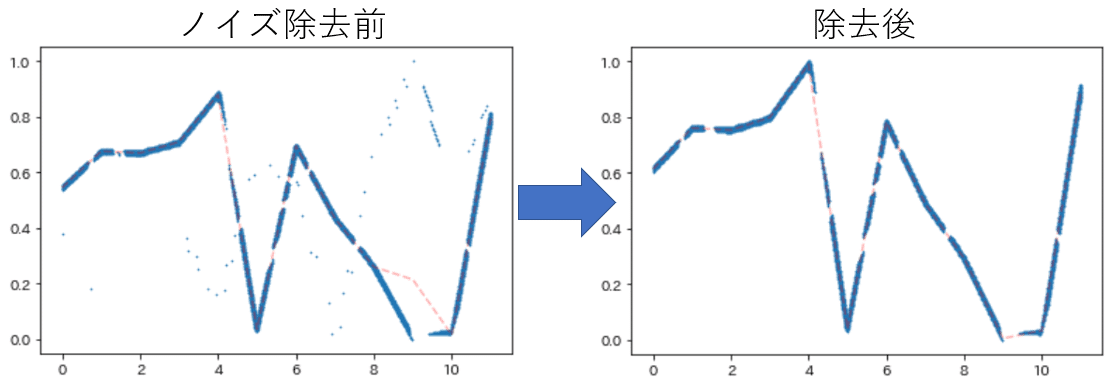
グレースケールなどの各色の差が小さい場合はアンチエイリアスで他の線の色として仕分けられてしまうため、データ化に悪影響を及ぼす。
対策として各折れ線の配列ごとで畳み込みを行い、
値が小さい=周囲にデータが存在しない=ノイズ
として除外することで、後述する線形回帰によるデータ化精度が上がった。
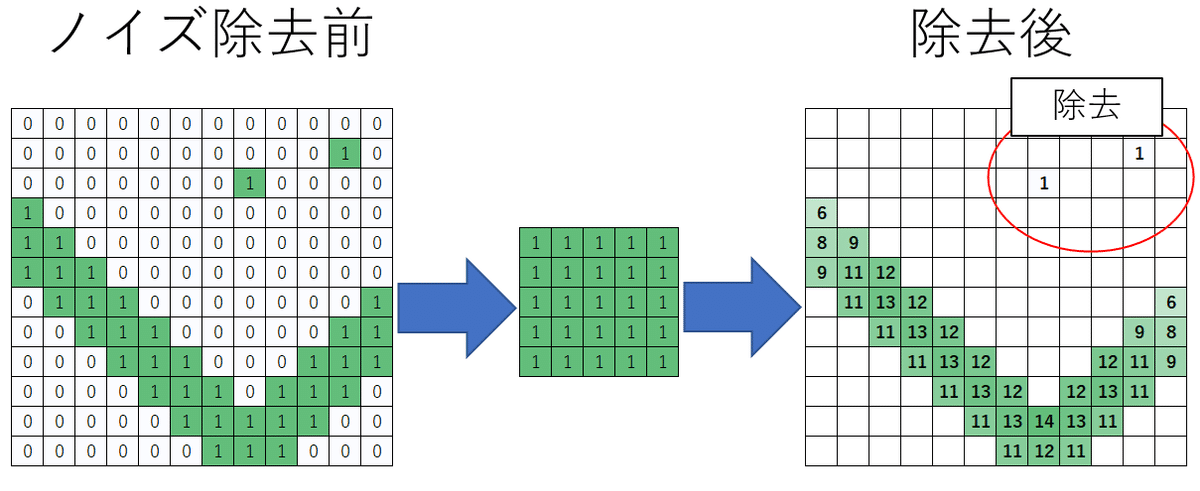
def opening(X,Y,minimum,kernel_shape = (5,5)):
"""
各折れ線のX,Y座標のリストに対してオープニング処理のようなものを行ったものを返す
(オープニング処理じゃなくなったけど)
Args
X:各折れ線ごとのX座標(,1)
Y:各折れ線ごとのY座標(,1)
minimum:範囲内のピクセルの数
kernel_shape:畳み込みするフィルターの形状(ky,kx)
returns:
X_new:ノイズ除去後の各折れ線ごとのX座標(,1)
Y_new:ノイズ除去後の各折れ線ごとのY座標(,1)
"""
#0~n_data-1の範囲だったものを整数に変換
X_base = np.int32(X*(x_max-x_min)/(n_data-1))
#オープニング処理用の配列
img_array = np.zeros((Y.max()+1,x_max-x_min+1),dtype=np.int32)
for x,y in zip(X_base,Y):
img_array[y][x] = 1
#【画像処理】Numpyで空間フィルタリング(畳み込み演算)
#https://qiita.com/aa_debdeb/items/e74eceb13ad8427b16c6
def padding(image, kernel_shape, boundary):
return np.pad(image, ((int(kernel_shape[0] / 2),), (int(kernel_shape[1] / 2),)), boundary)
def convolve2d(image, kernel):
shape = (image.shape[0] - kernel.shape[0] + 1, image.shape[1] - kernel.shape[1] + 1) + kernel.shape
strides = image.strides * 2
strided_image = np.lib.stride_tricks.as_strided(image, shape, strides)
return np.einsum('kl,ijkl->ij', kernel, strided_image)
pad_image = padding(img_array,kernel_shape,"edge")
conv_array = convolve2d(pad_image,np.ones(kernel_shape))
#折れ線ごとのx,y座標の配列にしたあとに画像の形に戻しているので二度手間かもしれない
XX,YY = np.meshgrid(np.arange(img_array.shape[1]),np.arange(img_array.shape[0]))
XX = XX.reshape(-1,1)
YY = YY.reshape(-1,1)
#オープニング処理後に残った座標
img_array2 = np.concatenate([conv_array.reshape(-1,1),XX,YY],1)
#(5,5)の範囲に合計minimumより多いピクセルがあればノイズではないとする
img_array2 = img_array2[img_array2[:,0]>=minimum]
base_idx = X_base*10000 + Y
opening_idx = img_array2[:,1]*10000 + img_array2[:,2]
X_new = X[np.isin(base_idx,opening_idx)]
Y_new = Y[np.isin(base_idx,opening_idx)]
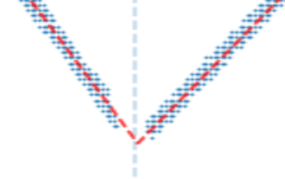
return X_new,Y_new折れ線が重なっている部分を線形回帰で補間
折れ線同士が重なって抽出が難しいこともあり、対処が必要。

データの座標の左側、右側それぞれで線形回帰を行い、
重なって隠れている部分の数値を予測させる。
from sklearn.linear_model import HuberRegressor
#データ点の周りプラスマイナスeの範囲のピクセルのy座標の中央値を取得する
#次のデータまでの距離を1とした場合の範囲
e = 0.01
algorithm = HuberRegressor #外れ値に頑健なアルゴリズム
line_pred_list = []
for i_line in range(n_line):
X_i = X_list[i_line]
Y_i = Y_list[i_line]
X_i,Y_i = opening(X_i,Y_i,minimum=4) #ノイズ削減のための処理
X_i = X_i.reshape(-1,1)
Y_i = Y_i.reshape(-1,1)/Y_i.max()
pred_list = []
for i_data in range(n_data):
#このデータは両端が必ず0で固定
if i_data in [0,n_data-1]:
pred_list.append(0)
continue
flg_ = (X_i>=i_data-e)&(X_i<=i_data+e)
if sum(flg_)>0:#近くにデータがあればデータを使用
pred_list.append(np.median(Y_i[flg_]))
continue
else:
#データが無ければ線形回帰して該当箇所を予測補間
pred_ = []
if i_data-1>=0:
#左側にあるピクセルで線形回帰
flg_L = (X_i>=i_data-1)&(X_i<=i_data)
X_L = X_i[flg_L].reshape(-1,1)
Y_L = Y_i[flg_L].reshape(-1,1)
if len(X_L)>10:
reg = algorithm().fit(X_L,Y_L)
pred = reg.predict(np.array([[i_data]]))
pred_.append(pred[0])
if i_data+1<=n_data:
#右側にあるピクセルで線形回帰
flg_R = (X_i>=i_data)&(X_i<=i_data+1)
X_R = X_i[flg_R].reshape(-1,1)
Y_R = Y_i[flg_R].reshape(-1,1)
if len(X_R)>10:
reg = algorithm().fit(X_R,Y_R)
pred = reg.predict(np.array([[i_data]]))
pred_.append(pred[0])
if len(pred_)==2:
#左側、右側の線形回帰を、データ数で重み付けして平均
pred_ = pred_[0]*len(X_L) + pred_[1]*len(X_R)
pred_ /= len(X_L)+len(X_R)
elif len(pred_)==1:
#左側、右側のみを線形回帰した場合
pred_ = pred_[0]
else:
#前後に全く同色がないため補間が困難。
pred_ = 0
pred_list.append(pred_)
line_pred_list.append(pred_list/sum(pred_list))データ化完了
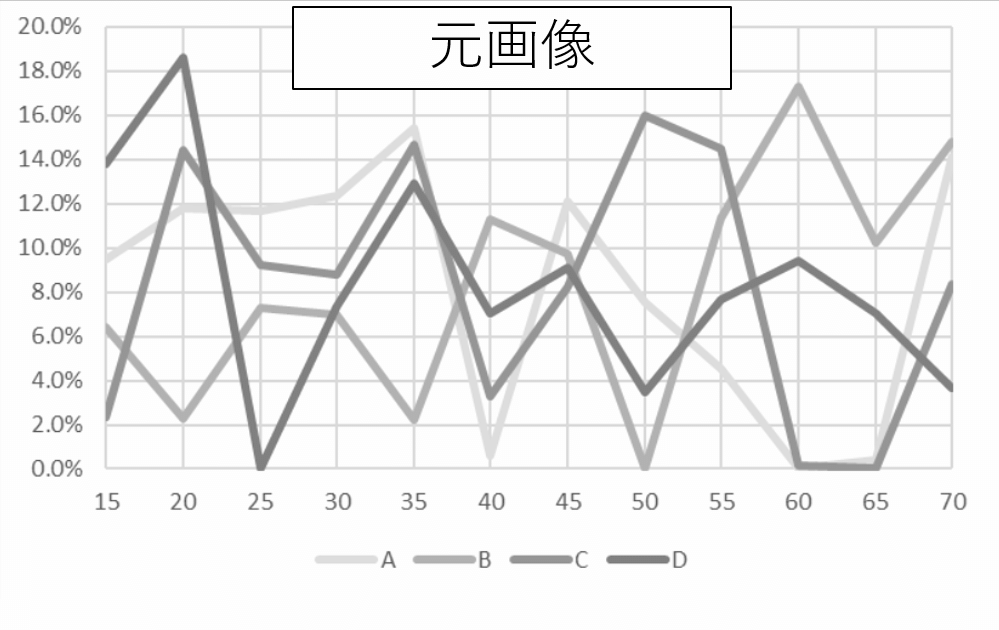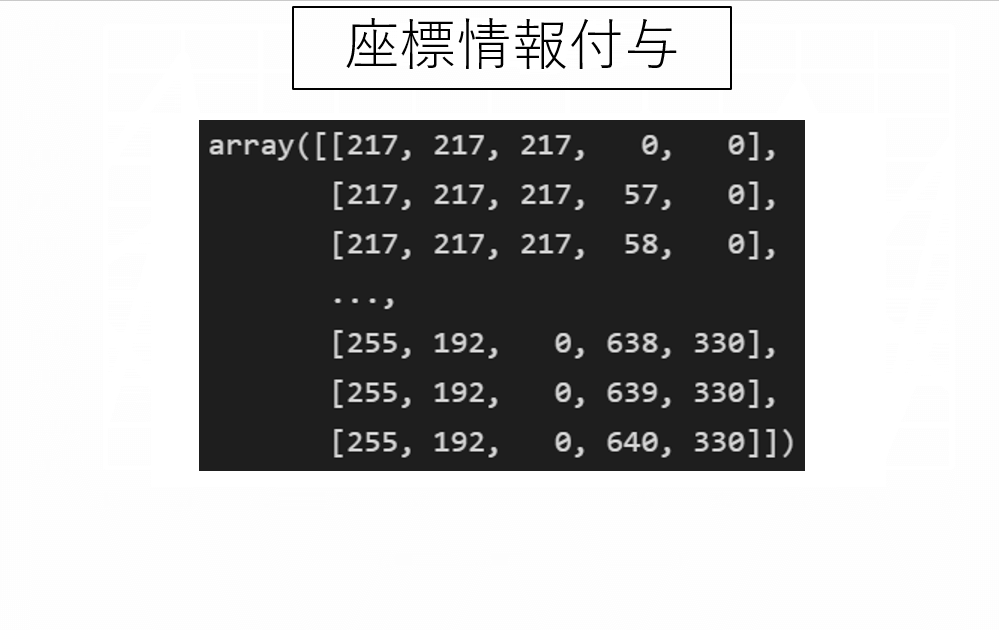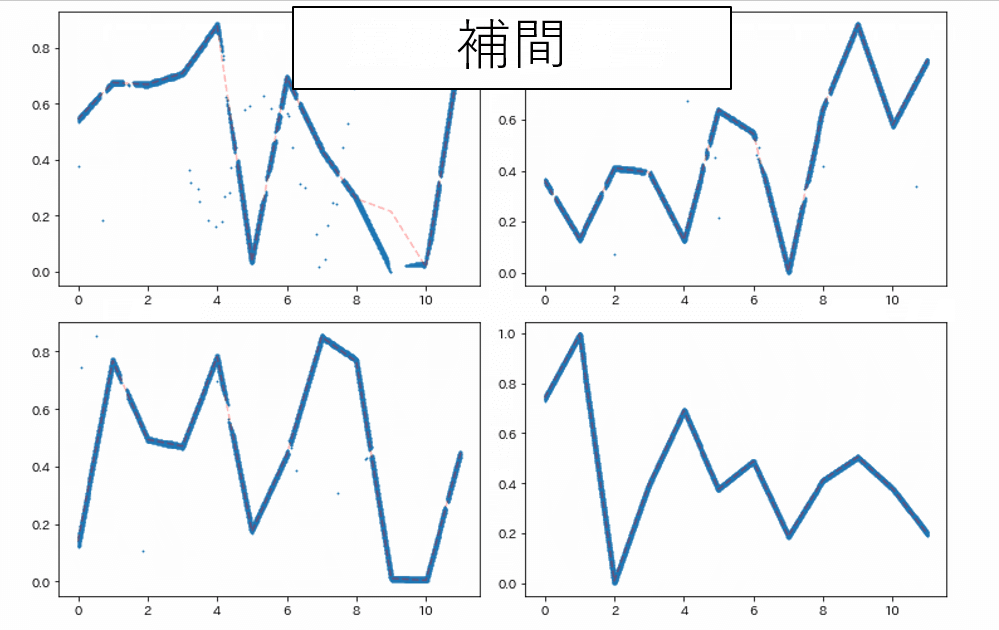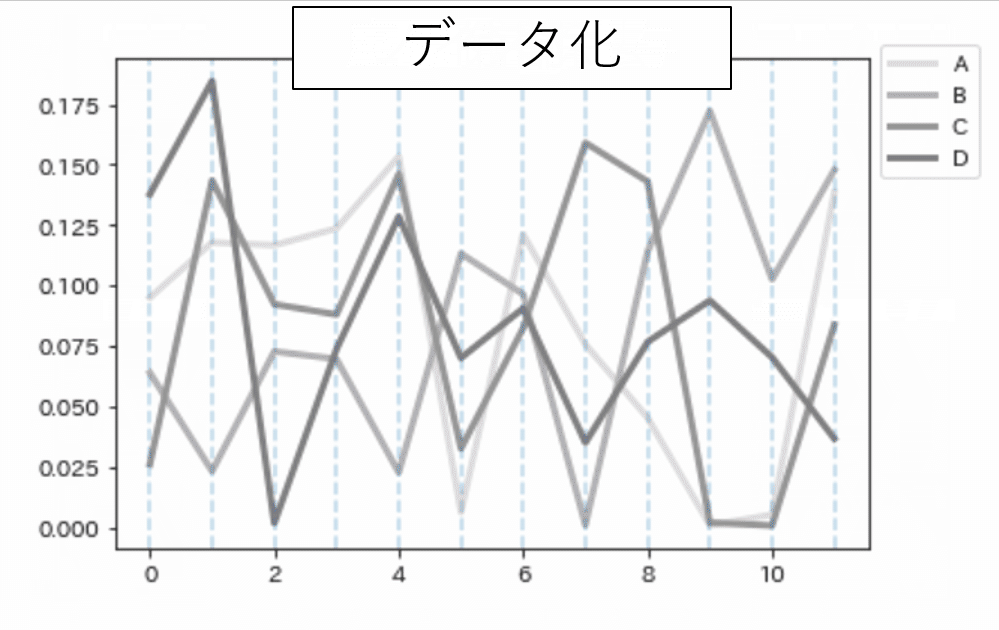
真の値とのズレはMAEで0.001986..と1%未満に収まった
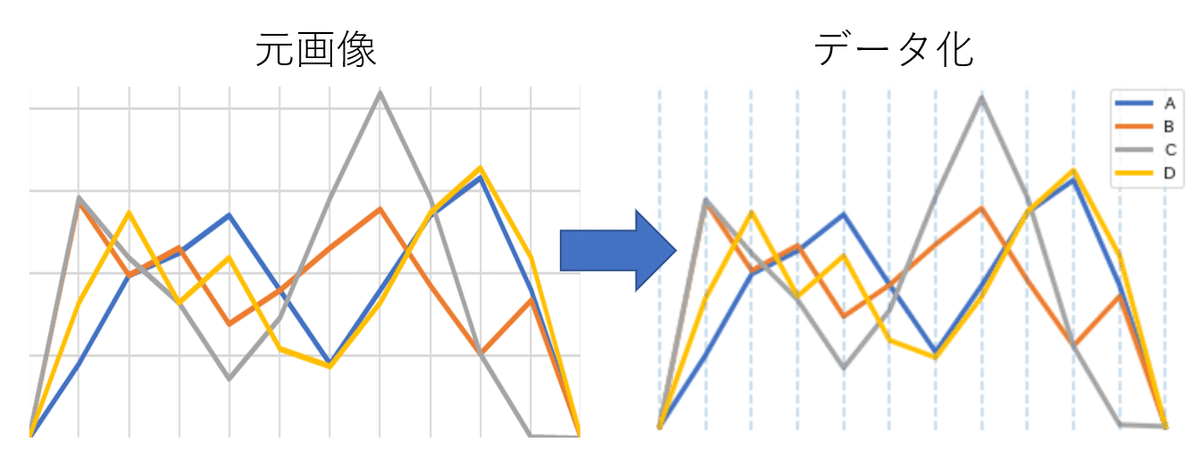
他の配色でも可能。グレースケールでも上手く行ったのは予想外でした。
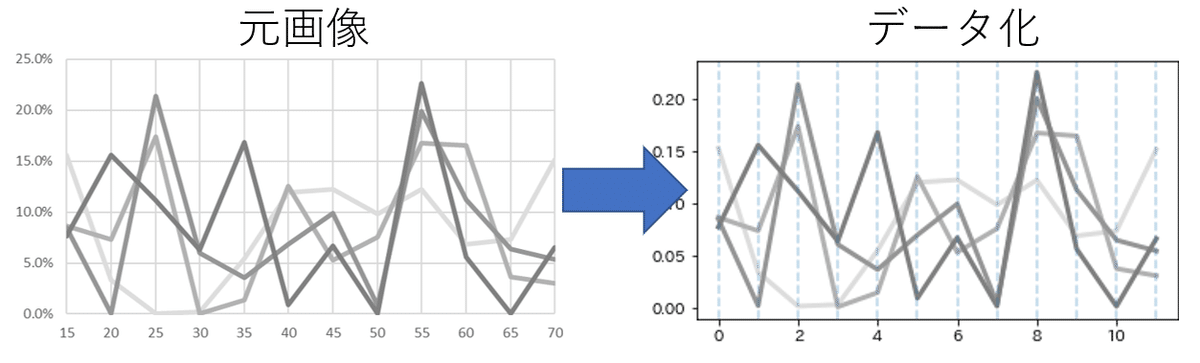
思いの外うまくやってくれた
データ化精度の検証
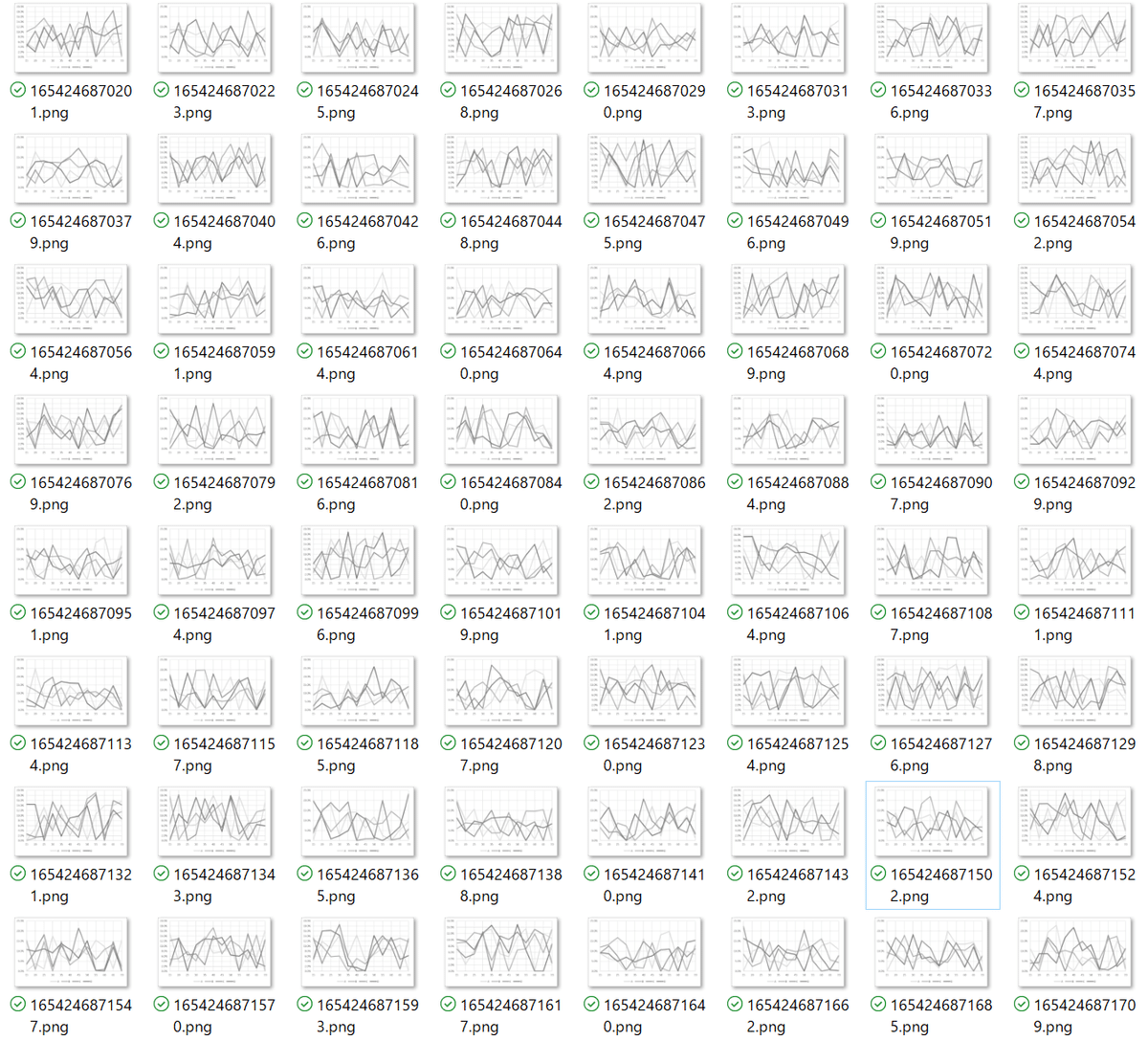
値を0~1の範囲の一様分布で出力後、合計1になるように正規化した4本の折れ線グラフを100枚EXCELからwin32com.clientを使用して抽出し、データ化精度を検証。
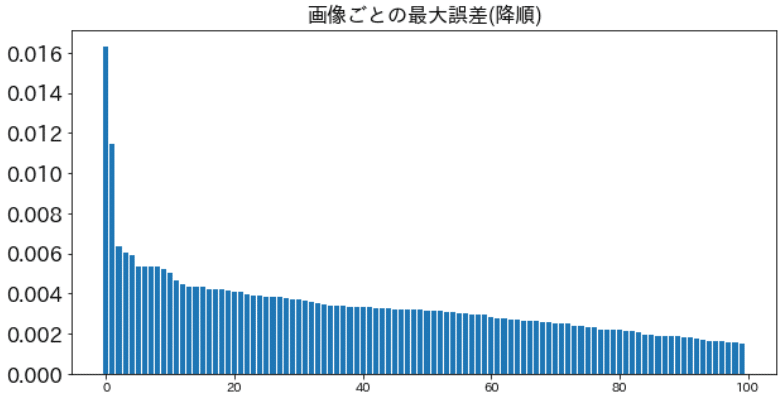
(わりと理想的にデータ化できている事が多かったので)MAEではなく、折れ線画像ごとでの最大の誤差で確認した。(下図)
多くは0.01未満の誤差で済んでいる。
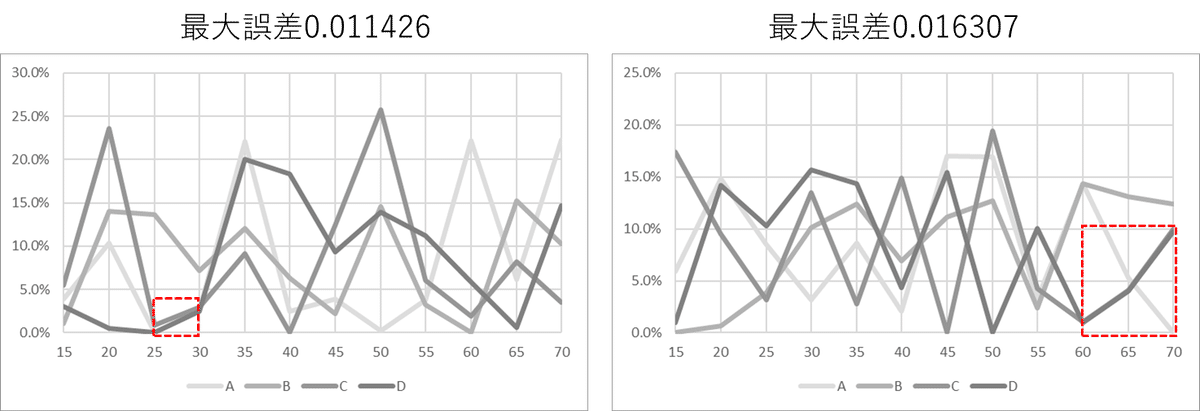
課題:完全に線が重なってしまった場合
先の集計で最大誤差が大きくなっていた画像は以下の2枚で、どちらも線が完全に重なっている領域が存在していた。
2つの線が完全に重なって下のピクセルが隠れているデータについての抽出方法も無くはないだろうが、今後の課題とする。
まとめ

画像化されたグラフのデータ化という、どれだけの人に役に立つかわからない内容について紹介したが、team_aiデータ分析技術部のメンバーによると、こうした作業が必要になることは多いらしい。
実はもっと様々な形式の画像化されたグラフに対応できるWebPlotDigitizerというアプリがあります。
このWebPlotDigitizerを試してみると解決するタスクも多いかもしれない。
座標軸が対数の場合や、折れ線グラフ以外でもデータ化が可能とのこと。
しかし、WebPlotDigitizerは手入力が必要で、画像一枚ごとに操作を行う必要があるようなので、画像化されたグラフのフォーマットが定まっている場合は私のようにデータ化を試みたほうがいいかもしれないです。
ぜひお試しください!
