
フェルマーの鸚鵡は… The Parrot's Theorem / Le Théorème du perroquet
The title of this article comes from a novel by French author Denis Guedj. Its Japanese translation has a title 『フェルマーの鸚鵡はしゃべらない』.


A week ago I read the book (in Japanese translation) which I bought about 20 years ago, most likely after my "resolution" to resume my study of mathematics after I get retired. Until recently, this book had been lying in the back of a bookshelf, but I was aware of a reference (in chapter 21) to the following counterexample by Noam Elkies to Euler's conjecture as a generalization of Fermat's Last Theorem:
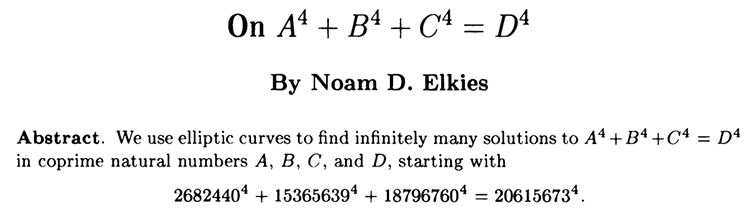
In the book "The Parrot's Theorem", this ⬆️ reference is contained in a fragment of cards by Grosrouvre who is already dead, but it clearly suggests that the story is before the completion of the proof of Fermat's Last Theorem (Dernier théorème de Fermat in French) by Andrew Wiles. This counterexample by Noam Elkies is explained in Wikipedia Euler's sum of powers conjecture.
This is a mystery
with intriguing technique taking us back to ancient Greece or medieval Persia yet also making us speculate what happened in the tropical rainforest in Brasil...where it is deemed highly unlikely to study modern mathematics in a magical world of Gabriel García Márquez's "One Hundred Years of Solitude"...though Brasil is not a Spanish speaking country...
Although the novel by Denis Guedj (1940 - 2010) was not written with the intention of being a history of mathematics, it does feature prominent Persian mathematicians in addition to Greek mathematicians.
While we collectively talk often about Pythagoras of Samos, Thales of Miletus, Archimedes of Syracuse, et al., I suspect we rarely refer to Persian mathematicians such as Muhammad ibn Musa al-Khwarizmi (780 - 850) or Nasir al-Din al-Tusi (1201 - 1274).

Omar Khayyam (1048 - 1131) is so famous thanks to Rubaiyat, but he was a prominent mathematician and most notable for his work on the classification and solution of cubic equations.

https://www.cyruscrafts.com/blog/information/omar-khayyam-the-life-story-poetry-and-philosophy-
It's not my intention to summarize the novel, but let me mention interesting facts randomly.
Chapter 5
In the books sent from Manaus, Brasil by Grosrouvre was the following standard textbook of elliptic curves, often called AEC:

In this chapter, another book "Local Class Field Theory" 『局所類体論』by Kenkichi Iwasawa 岩澤健吉 is mentioned as included in the books from Grosrouvre:

Kenkichi Iwasawa is known with Iwasawa Theory, which is mentioned in Wikipedia: Wiles's proof of Fermat's Last Theorem:
I was sitting at my desk examining the Kolyvagin–Flach method. It wasn't that I believed I could make it work, but I thought that at least I could explain why it didn't work. Suddenly I had this incredible revelation. I realised that, the Kolyvagin–Flach method wasn't working, but it was all I needed to make my original Iwasawa theory work from three years earlier. So out of the ashes of Kolyvagin–Flach seemed to rise the true answer to the problem. It was so indescribably beautiful; it was so simple and so elegant. I couldn't understand how I'd missed it and I just stared at it in disbelief for twenty minutes. Then during the day I walked around the department, and I'd keep coming back to my desk looking to see if it was still there. It was still there. I couldn't contain myself, I was so excited. It was the most important moment of my working life. Nothing I ever do again will mean as much.
Chapter 10
This chapter introduces Hypatia (350 or 370 - 415), a Neoplatonist philosopher, astronomer, and mathematician who lived in Alexandria, Egypt, then part of the Eastern Roman Empire. She was murdered in an abominable manner at the hand of a mob, behind which were clergymen who favored the Inquisition.
We recently observed such a mob in January 2021 incited by a convicted felon…😞
Chapter 12
Here comes philosopher René Descartes again regarding Amicable numbers.
[NOTE] In the Japanese translation, "Amicable number" is translated to 友数, but it's usually called #友愛数 in Japanese.
Amicable numbers were known to the Pythagoreans, who credited them with many mystical properties. A general formula by which some of these numbers could be derived was invented circa 850 by the Iraqi mathematician Thābit ibn Qurra (826–901). Other Arab mathematicians who studied amicable numbers are al-Majriti (died 1007), al-Baghdadi (980–1037), and al-Fārisī (1260–1320). The Iranian mathematician Muhammad Baqir Yazdi (16th century) discovered the pair (9363584, 9437056), though this has often been attributed to Descartes. Much of the work of Eastern mathematicians in this area has been forgotten.
Chapter 13
Muhammad ibn Musa al-Khwarizmi (780 - 850), often referred to as simply al-Khwarizmi, was a polymath who produced vastly influential Arabic-language works in mathematics, astronomy, and geography. His work Al-Jabr is the origin of algebra.

Chapter 17
The two main characters in this chapter are Niels Henrik Abel (1802 - 1829) and Évariste Galois (1811 - 1832), two mathematical geniuses who died young.
Let's recall that Fermat's Last Theorem has been proved using Galois representation on Elliptic curves, which are Abelian varieties, as a very high level description.
Chapter 21
This chapter starts with Goldbach's conjecture, one of the oldest and best-known unsolved problems in number theory and all of mathematics. In Chapter 25, a woman who has known Grosrouvre says "he told me that he would go to a river of gold to explore gold and diamond… He became a garimpeiro." Interestingly, Goldbach means a stream of gold.
The story of Paul Wolfskehl was new to me. He bequeathed 100,000 marks (equivalent to 1,000,000 pounds in 1997 money) to the first person to prove Fermat's Last Theorem with a condition that the prize had to be collected before September 13, 2007.
13092007 = 19 × 53 × 13001, but
1392007 is prime.
As mentioned earlier, this chapter refers to Noam Elkies. Just a few years ago, I encountered this mathematician in Joseph H. Silverman's AEC, which was introduced in Chapter 5 as one of gifts from Grosrouvre.

(via “The Arithmetic of Elliptic Curves” by Joseph H. Silverman)
and here is the latest result published in August 2024 with rank ≥ 29:
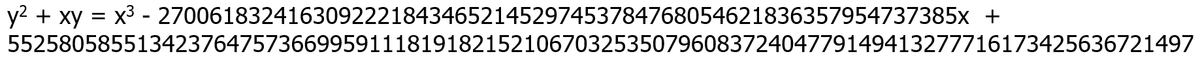
Chapter 25
Nofutur, the book's star parrot which had been suffering from amnesia, under a threat "Fermez-la !" (Shut your mouth!), brought back her memories and started shouting
"Fermez-la, Fermez-la, Fermat, Fermat…"
So the book should have been written in French!
Some association to other books
The way how Pierre Ruche (πR) talks to children reminds me of "Sophie's World" by Norwegian writer Jostein Gaarder, NOT "Sophie's Choice" by William Styron.
The way how to pursue hints given by a dead person reminds me of Gilbert Sinoué's "The Book of Sapphire" « Le Livre de saphir » in which theological historical mysteries and puzzles based on the three religions and their holy books are pursued in the Inquisition time in Spain.
In my favorite book "Dictionary of the Khazars" by Milorad Pavić, The Yellow Book (Hebrew source on the Khazar question), the following excerpt is noteworthy in terms of use of parrots to retain a language on the verge of oblivion:
The Islamic demon punished Princess Ateh by condemning her to forget her Khazar language and all her poems. She even forgot the name of her lover; all that her memory retained was the name of a fish-shaped fruit. But before this actually happened, Princess Ateh, sensing the coming danger, ordered a large number of parrots that could imitate human speech. One parrot was brought to the court for every word from The Khazar Dictionary, each was taught an entry from the book and could , at any time of night or day, recite by heart the lines referring to that word. Of course, since the verses were in Khazar language , this was the language in which the parrots recited them. When Khazar faith was abandoned and the Khazar language suddenly began to die out, Ateh released all the parrots versed in the Khazar dictionary. She told them, "Go and teach your poems to other birds, because soon nobody here will know them…." The birds flew away to the Black Sea forest, where they taught their poems to other parrots, and these taught them yet to others, until there came a moment when the poems and the Khazar language were known only to parrots. In the 17th century a parrot caught on the shores of the Black Sea could recite several poems in an incomprehensible language that its owner, a diplomat in Constantinople by the name of Avram Brankovich, claim to be the Khazar language…
Closing
A few months ago I read Laurent Binet's novel "The Seventh Function of Language" « La septième fonction du langage », while I greatly enjoyed the particular scene where the theme reveals at the end in a convincing manner, I was about to throw it in the trash because of obscenity of the language:

https://x.com/SokoKhazar/status/1766472293243605441
It's not appropriate to compare books, but I never felt so while reading Denis Guedj's "The Parrot's Theorem".
Photo credit: The header image via Pinterest.
P.S. Thanks to this "The Parrot's Theorem", I had the opportunity to do a little research on the famous Persian mathematicians.
For an obvious reason since Denis Guedj passed away in 2010, the novel does not refer to Maryam Mirzakhani (1977 - 2017), the first woman to receive the Fields Medal in 2014 in her research of Teichmüller theory, hyperbolic geometry, ergodic theory, and symplectic geometry.
I've not looked into her research, but it's a by-product of "The Parrot's Theorem" that I remembered my interest long time ago...
