
📏平均二乗誤差(MSE)は最小二乗法(LSM=S)をN分で割ったもの。 評価と推定
統計学では、(未観測量を推定する手順の)推定量の平均二乗誤差(MSE)または平均二乗偏差(MSD)は、誤差の二乗の平均、つまり推定値と実際の値の差の平均二乗を測定する。MSEはリスク関数であり、2乗誤差損失の期待値に対応する。MSEがほとんど常に厳密に正である(ゼロではない)という事実は、ランダム性のため、または推定器がより正確な推定値を生成できる情報を考慮していないためである。機械学習、特に経験的リスク最小化において、MSEは真のMSE(真のリスク:実際の母集団分布における平均損失)の推定値として、経験的リスク(観測されたデータセットにおける平均損失)を指す場合がある。
MSEは推定量の質を測る尺度である。ユークリッド距離の2乗から導かれるため,常に正の値であり,誤差がゼロに近づくにつれて減少する.
MSEは誤差の(原点に関する)2次モーメントであり、したがって推定値の分散(あるデータ標本から別のデータ標本まで推定値がどれだけ広く広がっているか)とバイアス(平均推定値が真値からどれだけずれているか)の両方が組み込まれている。 バイアスのかかっていない推定値の場合、MSEは推定値の分散である。分散と同様に,MSEは推定される量の2乗と同じ測定単位を持つ.標準偏差に類似して,MSEの平方根をとると,平均平方根誤差または平均平方根偏差(RMSEまたはRMSD)が得られ,これは推定される量と同じ単位を持つ; 不偏推定量では,RMSEは分散の平方根であり,標準誤差として知られている.
平均二乗誤差は、予測した値がどれくらい実際の値と違うかを示す指標で、その違いを2乗したものの平均です。
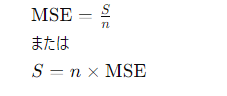
平均二乗誤差(Mean Squared Error, MSE)と最小二乗法(Least Squares Method)は密接に関連していますが、それぞれ異なる概念を表しています。以下でそれぞれの原理について説明します。
平均二乗誤差 (MSE)
定義: 平均二乗誤差は、予測値と実際の値の差(誤差)の二乗の平均です。これは予測モデルの性能を評価するために使用される指標の一つで、数値が小さいほどモデルの予測精度が高いことを意味します。
最小二乗法 (Least Squares Method)
定義: 最小二乗法は、データに最もよく適合する直線や曲線を見つけるための数学的手法です。これは、観測データと予測モデルとの間の二乗誤差の合計が最小になるようにモデルのパラメータを決定します。
目的: 誤差の二乗和を最小化することにより、最適なモデルパラメータを見つけ出します。これにより、予測値と実際の値の差が最小になるようにします。
関連性と違い
関連性: 両者は予測誤差を二乗して考えるという点で関連しています。最小二乗法は誤差の二乗和を最小化することで最適なモデルを見つける手法ですが、平均二乗誤差はそのようにして見つけたモデルの性能を評価するために使用されます。
違い: 最小二乗法はモデルのパラメータを推定するための手法ですが、平均二乗誤差は既に推定されたモデルの性能を評価する指標です。つまり、最小二乗法はモデルを構築する過程で使用され、MSEはモデルがどれだけよくデータを説明しているかを評価するために使用されます。
MSEと最小二乗法は、予測モデルのコンテキスト内で誤差を二乗するという共通点を持ちつつ、目的と適用範囲が異なります。最小二乗法は最適なモデルパラメータを見つけるために、MSEはそのモデルの性能を評価するために使われます。
MSEは予測値と実際の値との誤差を評価するために使用される指標です。式は次のようになります:
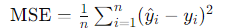
ここで、y^i は予測値、yi は実際の値、n はデータ点の数です。MSEは、誤差の二乗の平均を取ることで、大きな誤差を重く罰する特性があります。
LSM(最小二乗法)
LSMは一連のデータポイントに最もよくフィットするモデルパラメータを見つけるために使用される手法です。基本的には、次の誤差の二乗和を最小化します:
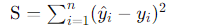
ここでも、y^i はモデルによる予測値、yi は実際の値です。LSMでは、この合計誤差の二乗和が最小になるようなパラメータを求めます。
import numpy as np
# 実際の値
y_true = np.array([1, 2, 3, 4, 5])
# モデルによる予測値
y_pred = np.array([1.1, 1.9, 3.05, 4.1, 4.8])
# 平均二乗誤差(MSE)の計算
mse = np.mean((y_true - y_pred) ** 2)
print(f"MSE: {mse}")
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# サンプルデータ
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 5, 4, 5])
# 最小二乗法で線形回帰モデルをフィット
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)
# モデルによる予測値
y_pred = slope * x + intercept
# 結果の表示
print(f"slope: {slope}, intercept: {intercept}")
plt.scatter(x, y, color='blue') # 実際のデータ点
plt.plot(x, y_pred, color='red') # フィットした線形モデル
plt.show()
違いの理解
MSEの計算例では、予測モデルの性能評価に焦点を当てています。予測値と実際の値との差を利用して、モデルがどれだけデータを正確に予測しているかを数値で示しています。
最小二乗法の例では、与えられたデータに基づいて最適な線形モデル(この場合は直線)を見つけることに焦点を当てています。これはモデルのパラメータ(傾きと切片)を推定する過程です。
この2つの例から、MSEがモデルの評価に、最小二乗法がモデルのパラメータ推定に使用されることがわかります。
\documentclass{article}
\usepackage{amsmath} % Package for mathematical symbols
\begin{document}
The formula for the Mean Squared Error (MSE) is given by:
\[
\text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2
\]
where $y_i$ represents the actual value for the \(i\)th observation, \(\hat{y}_i\) represents the predicted value, and \(n\) is the total number of observations.
\end{document}
(Chatgpt4にて出力で裏取り中)
最小二乗法は微分を活用しますね
はい、その通りです!最小二乗法では、与えられたデータに最もよく適合するパラメータを見つけるために、誤差(データとモデルの予測値との差)の二乗和を最小化します。この最小化問題を解くために微分が用いられ、偏微分を計算して勾配がゼロになる点を見つけます。これは、その点が最小値を与える点である可能性が高いことを意味します。
いいなと思ったら応援しよう!

