
📐冪級数展開について教えてください
冪級数展開は、ある関数を無限級数、特に冪級数で表現する方法です。無限級数は、無限個の項の和で構成されます。冪級数は、その項が変数の整数の冪で表される特殊な無限級数です。
一般的な冪級数の形は以下のように表されます。
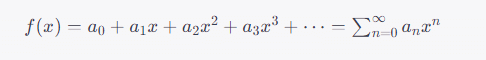
ここで、a0,a1,a2,… は定数で、x は変数です。
冪級数展開は、特定の点での関数の値と、その点での関数の導関数の値、2階導関数の値、などを使って、関数を冪級数で表現する方法です。
例えば、テイラー級数は、ある関数 )f(x) を、その関数の導関数、2階導関数、などの値を使って冪級数で表現する方法です。テイラー級数の一般的な形は以下のようになります。

ここで、f(n)(a) は、関数 f(x) の n 階導関数の x=a での値です。
テイラー級数を使って、多くの関数(例えば、指数関数、対数関数、三角関数など)を冪級数で表現することができます。ただし、すべての関数が冪級数で表現できるわけではありません。関数が特定の条件(例えば、滑らかであること、無限回微分可能であることなど)を満たす場合に、その関数を冪級数で表現することができます。
級数は、数学の歴史の中で様々な背景で発見され、多くの異なる目的で利用されてきました。
3世紀 BCE: アルキメデス
円の面積を求めるために、無限に接近する多角形の面積を求める方法を発表。https://editor.p5js.org/setapolo/sketches/HZ25f6syx
17世紀: ボノヴェントゥーラ・カヴァリエリ
無限小量の概念を発展させ、その概念を用いて面積と体積を計算する方法を発表。
17世紀: ガリレオ・ガリレイ
速度と距離に関連する級数の問題を研究。
17世紀: ジョン・ウォリス
"Arithmetica Infinitorum" (1656) で、円周率 π の逆数に関連する無限級数を発表し、他の多くの重要な結果も発表。
17世紀: アイザック・ニュートン
"Method of Fluxions" で微分法を発展させ、"Philosophiæ Naturalis Principia Mathematica" で、微分法と積分法を用いて天体の運動を説明。
17世紀: ゴットフリート・ライプニッツ
微分法と積分法を独立に発展させ、今日使われている多くの記号法を発表。
18世紀: 18世紀には、レオンハルト・オイラーが、級数展開を用いて多くの重要な数学的発見をしました。例えば、彼は、指数関数、三角関数、対数関数の級数展開を使って、複素数に関連する有名なオイラーの公式を発表しました。
19世紀以降: 19世紀以降、級数の理論はさらに発展しました。例えば、カール・ワイエルシュトラスは、級数の収束性に関連する重要な定理を発表しました。

変数のべきを「マトリョーシカ」に例えるのは面白い比喩かもしれません。マトリョーシカ人形は、大きな人形の中に小さな人形が次々と収められているロシアのお土産で、外側から内側へとサイズが小さくなっていくことが特徴です。この概念を変数のべきに適用すると、次のように解釈できます:
各「xn」(変数のべき乗)は、それぞれ異なる「層」または「レベル」を表していて、n の値が大きくなるにつれて、その影響や寄与(級数展開の文脈で)も異なります。
例えば、x1 は x 自身を、x2 は x の二乗を表し、それぞれが関数の挙動に異なる寄与をします。
級数展開においては、x0(常に1)から始まり、x1,x2,… という形で「層」が積み重なっていきます。これによって、元の関数 f(x) の近似が徐々に精密になっていく様子を表します。
このように、「マトリョーシカ」の比喩は、変数のべきの異なる項がどのように全体の関数を構成しているかを視覚的に表現するのに役立つかもしれません。ただし、数学的な厳密さではなく、概念の理解を助けるための比喩としての価値があります。
いいなと思ったら応援しよう!

