🛠️コンビネータ入門

2020年12月30日 11:05

厳密な関数型プログラミングとラムダ計算では、関数（ラムダ式）は状態を持たず、関数を囲む関数の引数のみを参照することが許される。

このため、関数が変数の状態に関連付けられ、この変数の状態が関数本体で使われるという、通常の再帰関数の定義は除外される。

Yコンビネータはそれ自体がステートレス関数であり、ステートレス関数に適用するとその関数の再帰バージョンを返す。

Yコンビネータは、固定小数点コンビネータと呼ばれるこの種の関数の中で最も単純なものである。

https://rosettacode.org/wiki/Y_combinator

関数型プログラミングでは、再帰をサポートしないプログラミング言語で再帰関数を正式に定義するために、Yコンビネータを使用することができます。

ラムダ計算においては、直接的な自己参照（つまり関数が自分自身を呼び出すこと）が禁止されています。しかし、再帰的な動作が計算の多くに必要です。この制約の中で再帰的な動作を実現するために、Yコンビネータのような技巧が用いられます。

具体的には、Yコンビネータは「再帰する関数を生成する関数」を受け取り、実際に再帰する関数を返す役割を持ちます。Yコンビネータを利用することで、ラムダ計算内で再帰的な動作を持つ関数を定義・利用することができます。

Yコンビネータはそれ自体がステートレス関数であり，別のステートレス関数に適用されると，その関数の再帰的なバージョンを返します．Yコンビネータは，固定小数点コンビネータと呼ばれるこの種の関数の中で最も単純なものです．

ステートレスYコンビネータを定義し、他のステートレス関数やラムダ式から階乗数やフィボナッチ数を計算しますと

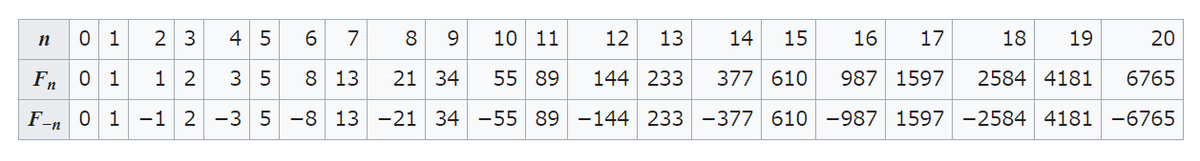
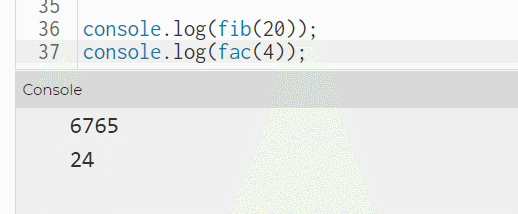
階乗はでかい数でもやった。

とりあえず、やる気をだすために、リファクタリングする。といっても関数名を短縮名から長い名前に変えるだけ。

var factorial = Y(function(f) {
   return function (n) {
       return n > 1 ? n * f(n - 1) : 1;
   };
});
var fibonacci = Y(function(f) {
   return function(n) {
       return n > 1 ? f(n - 1) + f(n - 2) : n;
   };
});

名前を変えると影響範囲が分かってくる。基本は関数Yを通して、新しい関数を作っているしくみのようだった。であれば、Yの中身を見ればいいが、もともとややこしいので、そのまま引数だけ見ると、Fを引数としてnを引数とした関数を戻り値にする関数がYの引数であることが分かる。

function Y(f) {
   var g = f((function(h) {
       return function() {
           var g = f(h(h));
           return g.apply(this, arguments);
       }
   })(function(h) {
       return function() {
           var g = f(h(h));
           return g.apply(this, arguments);
       }
   }));
   return g;
}

つまりここでの引数fは「nを引数とした関数を戻り値にする関数」であると意識しながらY自体はgを戻り値にしていて、gはhを引数としてとある関数を戻り値にする関数を引数にしたfでありfは「nを引数とした関数を戻り値にする関数」なのでなんとなくだがとある関数というのが、うまいことするとシーソーみたいに動くのかなというのは何と無しに分かる。

一度固有の処理に戻る。再帰的なセオリーで書かれているのが分かる。

var fibonacci = Y(function(f) {
   return function(n) {
       return n > 1 ? f(n - 1) + f(n - 2) : n;
   };
});

nが1以下になったら結果を返すけどそれまではfを呼び出すことになる。繰り返すが「nを引数とした関数を戻り値にする関数」である。そんであのシーソー部分を冷静に見る。ダブルドラゴンと名付けた。

gは「hを引数としてとある関数を戻り値にする関数」を引数にしたfでこれはYの戻り値になるわけだが、この「とある関数」は引数にした関数hを引数にした結果をfで処理した結果を実行して返すのが引数も関数なのでこちらの引数をも「とある関数」とする。

と、再帰するらしい。。。。

要るか、これ？

一つ思ったのは、顕著に言語系によって構成が変わるところで、きれいに読めるのは毎度おなじみのピコリスプだった。こんな感じ

(de Y (F)
  (let X (curry (F) (Y) (F (curry (Y) @ (pass (Y Y)))))
     (X X) ) )

美しい。。。

そしてコード博覧会、まずはここで腕力魅せるジュリア

julia> """
      # Y combinator
      * `λf. (λx. f (x x)) (λx. f (x x))`
      """
      Y = f -> (x -> x(x))(y -> f((t...) -> y(y)(t...)))

記号で攻めてきた

APL勢　Joy J

Y=. '('':''<@;(1;~":0)<@;<@((":0)&;))'(2 : 0 '')
 (1 : (m,'u'))(1 : (m,'''u u`:6('',(5!:5<''u''),'')`:6 y'''))(1 :'u u`:6')
)

こっちがジェイ

DEFINE y == [dup cons] swap concat dup cons i;
    fac == [ [pop null] [pop succ] [[dup pred] dip i *] ifte ] y.

こっちがジョイ

LISP系をもう一度、クロージャとかとか

(defn Y [f]
 ((fn [x] (x x))
  (fn [x]
    (f (fn [& args]
         (apply (x x) args))))))
(def fac
    (fn [f]
      (fn [n]
        (if (zero? n) 1 (* n (f (dec n)))))))
(def fib
    (fn [f]
      (fn [n]
        (condp = n
          0 0
          1 1
          (+ (f (dec n))
             (f (dec (dec n))))))))

これがクロージャ

(defun Y (f)
 ((lambda (g) (funcall g g))
  (lambda (g)
    (funcall f (lambda (&rest a)
		  (apply (funcall g g) a))))))
(defun fac (n)
 (funcall
  (Y (lambda (f)
      (lambda (n)
        (if (zerop n)
	   1
	   (* n (funcall f (1- n)))))))
  n))
(defun fib (n)
 (funcall
  (Y (lambda (f)
      (lambda (n a b)
        (if (< n 1)
          a
          (funcall f (1- n) b (+ a b))))))
  n 0 1))
? (mapcar #'fac '(1 2 3 4 5 6 7 8 9 10))
(1 2 6 24 120 720 5040 40320 362880 3628800))
? (mapcar #'fib '(1 2 3 4 5 6 7 8 9 10))
(1 1 2 3 5 8 13 21 34 55)

コモンリスプ

 (define Y
   (lambda (X)
     ((lambda (procedure)
        (X (lambda (arg) ((procedure procedure) arg))))
      (lambda (procedure)
        (X (lambda (arg) ((procedure procedure) arg)))))))
; Fib
(define Fib* (lambda (func-arg) 
   (lambda (n) (if (< n 2) n (+ (func-arg (- n 1)) (func-arg (- n 2)))))))
(define fib (Y Fib*))
(fib 6)
   → 8
; Fact
(define F*
  (lambda (func-arg) (lambda (n) (if (zero? n) 1 (* n (func-arg (- n 1)))))))
(define fact (Y F*))
(fact 10)
   → 3628800

エコーリスプ

短く書けてる系REBOL Ruby

Y: closure [g] [do func [f] [f :f] closure [f] [g func [x] [do f :f :x]]]

みやすい

y = lambda do |f|
 lambda {|g| g[g]}[lambda do |g|
     f[lambda {|*args| g[g][*args]}]
   end]
end
fac = lambda{|f| lambda{|n| n < 2 ? 1 : n * f[n-1]}}
p Array.new(10) {|i| y[fac][i]}   #=> [1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
fib = lambda{|f| lambda{|n| n < 2 ? n : f[n-1] + f[n-2]}}
p Array.new(10) {|i| y[fib][i]}   #=> [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]

こちらはrubyでさすが

let fix f g = (fun x a -> f (x x) a) (fun x a -> f (x x) a) g

Ocaml　APL勢とは違った安定性

Y:     parse arg Y _;                     $=             /*the  Y  combinator.*/
        do j=1  for words(_); interpret '$=$' Y"("word(_,j)')';end;    return $

REXX

善戦したsmalltalk

Y := [:f| [:x| x value: x] value: [:g| f value: [:x| (g value: g) value: x] ] ].
fib := Y value: [:f| [:i| i <= 1 ifTrue: [i] ifFalse: [(f value: i-1) + (f value: i-2)] ] ].
(fib value: 10) displayNl.
fact := Y value: [:f| [:i| i = 0 ifTrue: [1] ifFalse: [(f value: i-1) * i] ] ].
(fact value: 10) displayNl.

small talk

ポイントフリー (Point-free):
- この「ポイント」とは、具体的な引数やデータの「点」を指すことが多い。ポイントフリースタイルでは、関数の定義において具体的な引数を使わないことからこの名前がつけられました。
固定小数点 (Fixed-point):
- この「ポイント」は、数学的な「固定点」を指します。関数f(x)に対して、f(x) = x となるxの値を固定点と言います。固定小数点コンビネータは、この固定点を見つけるためのツールとして使われることが多い。

いいなと思ったら応援しよう！

お願い致します