🔮SICP ｢計算機プログラムの構造と解釈｣は時代遅れの本なのか？

2021年5月1日 13:23

表紙に魔術師が描かれているため魔術師本（Wizard Book）としても知られ、まれに表紙の色をとって紫本（Purple Book）とも呼ばれている。

私たちは呪文によってコンピュータの精霊を呼び出しているのだ。

これから計算過程というものを勉強します。計算プロセスは、コンピュータに生息する抽象的な存在である。プロセスは進化しながら、データという他の抽象的なものを操作していきます。プロセスの進化は、プログラムと呼ばれるルールのパターンによって指示される。人間は、プログラムを作ってプロセスを指示する。つまり、私たちは呪文によってコンピュータの精霊を呼び出しているのだ。

https://sourceacademy.org/sicpjs/1

JavaScriptで登場

今回は、背景が暗いJavaScriptの文をマウスでクリックすると、JavaScriptのインタプリタが表示され、その文を評価して結果の値を表示できるようにプログラムされています。

https://sourceacademy.org/sicpjs/1.1.1

データとはなにか

一般に, データは選択子と構成子と, これらの手続きを有効な表現とするために満たすべき条件とで定義されると思ってよい

この一節で言いたいことは、プログラミングにおける「データ」とは、単なる値や情報の集まりではなく、そのデータを操作するための手続き（関数やメソッド）と、それら手続きが正しく機能するためにデータが満たすべき条件（制約やルール）を含んで定義されるべきであるということです。

具体的には、「選択子」とはデータから特定の部分を取り出すための手続き、「構成子」とはデータを作り出すための手続きを指します。これらの手続きが正しく動作するためには、データは一定の構造や形式を持っている必要があります。この「満たすべき条件」がその構造や形式に当たります。

要するに、データはそれ自体の構造と、それに関連する操作（手続き）の両方を考慮して定義されるべきである、ということが述べられています。

はあ

驚くべきことにこの考えを厳密に形式化するのは非常に難しい. 形式化に二つの方法がある. 一つは C.A.R.Hoare(1972)が開拓したもので,「手続きと条件」の規定で形式化する、抽象モデル(abstract model)の方法として知られている.

はあ

もう一つの方法はMITの Zilles, IBMの Goguen, Thatcher, Wagnerおよび Wright(Thatcher, Wagner and Wright 1978参照)とトロントのGuttag (Guttag 1977参照)が導入したもので, 代数的仕様(algebraic specification)という. これはわれわれの「条件」に対応する公理でシステムの行動を規定する抽象代数システムの要素として「手続き」を見, データオブジェクトに対する表明を検査するのに抽象代数の手法を使う

Specification Techniques for Data Abstractions

データ抽象化のための仕様化技術

本書のアプローチは大きく「手続きによる抽象の構築」と「データによる抽象の構築」からなる。

ストーリームと遅延評価

図3.32に示す加算器のフィードバックループは, integralの内部ストリームintが, それ自身を使って定義してあるという事実によってモデル化されている:
(define int
(cons-stream initial-value
(add-streams (scale-stream integrand dt)
int)))
このような暗黙の定義を扱う解釈系の能力はcons-streamに組み込まれているdelayに依存している. このdelayがないと, 解釈系はcons-streamの二つの引数を評価する前にintを構成することが出来ない. 引数の評価はintが既に定義されていることを要求する. 一般にdelayはループを含む信号処理システムをストリームを使ってモデル化するのに重要である. delayがないとわれわれのモデルは, 信号処理要素への入力は出力が作られる前に完全に評価されるように形式化しなけばならない. これはループには使えない.

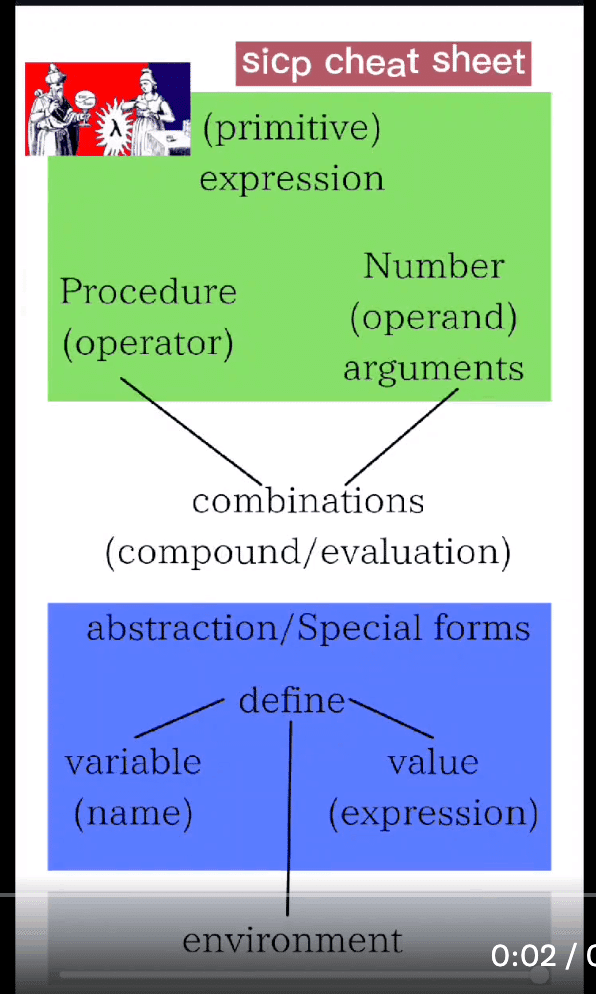
オブジェクト指向から関数型プログラミングへの橋渡しとしてのsicp

SICPはオブジェクト指向プログラミング（OOP）と関数型プログラミング（FP）の両方の概念を取り上げていますが、主に関数型プログラミングの観点からアプローチしています。それによって、オブジェクト指向プログラミングの背景を持つ読者にとって、関数型プログラミングの理解への橋渡しとなる可能性があります。

以下は、SICPがどのようにこれらの二つのアプローチを統合するのかを示すポイントです：

関数型プログラミング: SICPはSchemeという純粋な関数型プログラミング言語を使用しています。そのため、本を読むことで、不変性、再帰、高階関数、ラムダ計算などの関数型プログラミングの核心的な概念に触れることができます。
オブジェクト指向プログラミング: 本の後半部分では、オブジェクト指向のアイディアを取り入れたデータ抽象化や状態の持つオブジェクトの概念を導入します。これにより、メッセージパッシングや状態のカプセル化といったOOPの基本的な考え方を学ぶことができます。
統合: SICPは、これらの異なるアプローチを組み合わせて、強力な抽象化やモジュール化の手法を提供します。この統合的なアプローチにより、OOPとFPの間のギャップを埋めるのに役立つ洞察や概念を得ることができます。

したがって、SICPはオブジェクト指向プログラミングの背景を持つ読者にとって、関数型プログラミングへの適切な導入となり得ます

Sicpにはモナドとかコンビネータは出てこないですか？

『計算機プログラムの構造と解釈』（Structure and Interpretation of Computer Programs、略称SICP）は、コンピュータサイエンスの基礎を教えるための教科書で、MITで長年にわたって使用されてきました。この教科書は主にScheme言語を使用して、計算のプロセス、抽象化、再帰、解釈器の設計などの概念を説明しています。

SICPでは、モナドやコンビネータといった概念は直接的には取り扱われていません。これらのトピックは関数型プログラミングやカテゴリ理論におけるより高度な概念であり、SICPがカバーする範囲を超えています。SICPの目的は、プログラミングの基礎とコンピュータサイエンスの根本的な理論に焦点を当てることであり、その過程でSchemeを用いた高度なプログラミング技術を紹介することにありますが、モナドやコンビネータはそれらの一部として扱われていません。

モナドやコンビネータは、Haskellなどの他の関数型プログラミング言語を扱う文脈でより頻繁に議論されるトピックです。これらの概念に興味がある場合は、関数型プログラミングやカテゴリ理論に特化した別の教材やリソースを探求することをお勧めします。

Sicpは関数型の説明は1部ありますか？

はい、SICP（『計算機プログラムの構造と解釈』）には関数型プログラミングに関する説明が含まれています。実際、SICPは関数型プログラミングの基礎的な概念を学ぶための優れた資料の一つとされています。この教科書では、Scheme言語を用いて、再帰、高階関数、関数を第一級オブジェクトとして扱うこと、ラムダ計算の概念など、関数型プログラミングの核心的なアイデアを教えています。

SICPの最初の部分では、プログラムを手続きとして捉える代わりに、数学的関数として理解することの重要性を強調しています。この観点から、プログラムは入力を受け取り、何らかの出力を生成する数学的な関数と見なされます。このようなアプローチは、副作用を避け、よりシンプルで理解しやすいコードを書くための基礎となります。

SICPでは、これらの概念を通じて、計算の本質を理解し、より良い抽象化を構築する方法を学びます。関数型プログラミングのスタイルは、プログラムのモジュール性と再利用性を高めることに貢献すると共に、複雑なシステムをよりシンプルに分解するための強力なツールを提供します。

したがって、SICPは関数型プログラミングの原則を理解し、それらを実践的に適用する方法を学ぶのに非常に適した資料です。

SICP (Structure and Interpretation of Computer Programs) では、モナドに関する具体的な解説はありませんが、モナド的な考え方に近い内容としては、クロージャーに関する部分や、状態を扱うための環境モデル、ストリーム処理、継続などが挙げられます。

特にクロージャーの概念は、モナドの「バインド」操作に似た側面を持ち、関数を利用して状態や文脈を持続的に扱う方法として理解できます。また、SICP で紹介されるストリームや継続も、モナドの基本概念に通じる部分があります。ストリーム処理は、データの流れを管理する点でモナド的な要素を持ち、継続は計算の文脈を扱うため、特定のモナドの実装に近い考え方です。

モナドに関する具体的な理解を深めるためには、SICPのこれらのセクションを基に、Haskellのような言語でモナドを学ぶと、よりモナドの概念が明確になるでしょう。

いいなと思ったら応援しよう！

お願い致します

🔮SICP ｢計算機プログラムの構造と解釈｣ は時代遅れの本なのか？